Исследование природы темнового счета сверхпроводникового однофотонного детектора

Принцип работы сверхпроводникового однофотонного детектора. [1] (Superconducting Single-Photon Detector, SSPD) основан на. переходе небольшого участка, сверхпроводящей полоски нитрида, ниобия (NbN) в резистивное состояние при поглощении фотона. [2]. Полоска смещается током, поэтому переход её части в резистивное состояние сопровождается импульсом напряжения, который может быть зарегистрирован. Переход участка, полоски в резистивное состояние может быть инициирован как поглощением фотона, так и флуктуацией. Такими флуктуациями могут быть, например, термически активированные одиночные вихри, пересекающие полоску поперёк направления тока. Настоящая работа посвящена, исследованию зависимости числа, флуктуационных (темновых) срабатываний SSPD от тока смещения и температуры и сравнении её с предсказаниями модели термически активированных одиночных вихрей.

В последние годы SSPD нашли широкое применение во многих отраслях прикладной науки, таких как квантовая криптография [3, 4], исследования однофотонных источников оптического излучения [5, 6] и измерения запутанных состояний фотонов [7]. Большой интерес к этому виду детекторов обусловлен тем, что SSPD обладают высокими показателями по следующим параметрам: эффективность детектирования, быстродействие, малая нестабильность переднего фронта, импульса, (малый джиттер), низкий уровень темнового счета.

Известным экспериментальным фактом является связь квантовой эффективности с величиной рабочего тока, детектора. [8]. С одной стороны, чем ближе мы подходим к величине критического тока, тем больше становится эффективность детектирования. С другой стороны, по мере роста тока смещения начинает расти и темновой счет детектора, что приводит к уменьшению отношения сигнал-шум, поскольку темновой счет растет с током быстрее эффективности детектирования. При токах смещения, близких к величине критического тока, уровень темнового счета, может достигать значений в несколько мегагерц, что уничтожает одно из основных достоинств SSPD и является весьма, критичным при работе со слабыми оптическими пучками (однофотонные источники, квантово-криптографические линии связи). Экранирование детектора, от внешних шумов и засветки практически не влияет на. уровень темнового счета, поэтому естественно предположить, что наличие темнового счета в SSPD связано с флуктуациями в самой сверхпроводящей полоске.

3.    Теоретическая часть

На данный момент существует несколько моделей, описывающих природу темнового счета в SSPD, но в рамках этой работы мы будем использовать всего одну модель - модель перескока одиночных термически активированных вихрей через потенциальный барьер на входе в сверхпроводник. Кратко опишем основные идеи этой модели, предложенной в [9] и развитой в [10], а также в [11].

Тонкую сверхпроводящую пленку нитрида ниобия, из которой сделан детектор, можно рассматривать как двумерную систему, так как она удовлетворяет следующим условиям: d ~ ф X2D >> to >> ф где d - толщина пленки (4 нм), to - ширина полоски (100 нм), ф - длина когерентности (4 нм [12]), А20 - пирловская длина (~ 50 мкм [10]). Для систем такого рода возможно флуктуационное проникновение одиночных абрикосовских вихрей в пленку через край полоски [13, 14]. Появившийся вихрь начинает взаимодействовать с магнитным полем тока смещения, прикладываемого к образцу, что выражается силой Лоренца, действующей на вихрь. Под действием силы Лоренца вихрь движется в направлении, перпендикулярном току, от одного края сверхпроводящей полоски к другому краю; этот процесс сопровождается выделением энергии. Оценки, а также численные расчеты на основании времязависимого уравнения Гинзбурга-Ландау [11], показывают, что при длине когерентности ф и длине термализации tth, характерных для пленок NbN, этой энергии достаточно для существенного (возможно, даже полного) подавления параметра порядка в «следе» вихря. Таким образом, после прохождения вихря образуется область шириной порядка 1th ~ 20 нм, пересекающая всю полоску, в которой критическая плотность тока существенно понижена по сравнению с остальной пленкой и ниже плотности тока смещения полоски, поэтому в этой области появляется сопротивление. Образовавшись, резистивная область будет поддерживаться и даже увеличиваться в размерах за счет диссипации энергии транспортного тока, до тех пор, пока последний не будет вытеснен в шунтирующую детектор нагрузку [15, 16], подобно тому, как это происходит при детектировании фотона. Поэтому каждое событие флуктуационного вхождения вихря будет сопровождаться таким же импульсом напряжения, как и при регистрации фотона, т.е. будет вызывать темновой отсчет.

Вероятность вхождения вихря в единицу времени вычислена в работе [10]. Предполагая, что каждое событие вхождения вихря сопровождается появлением резистивного состояния и регистрацией импульса напряжения, авторы [10] получили следующее выражение для числа темновых отсчетов SSPD в единицу времени D _cps:

Dcps ■ (Іь/ІсТ,И)

где Iь ^ ток смещения детектора, 1с - критической ток, v = ео/кТ,(2)

где к - постоянная Больцмана, Т - температура детектора, ео - характеристическая энергия вихря. Последняя дается выражением ео = (Ф0 ^2)/(47tLS9 ),(3)

где Фо - квант магнитного потока, ц - коэффициент, описывающий подавление параметра порядка за счёт распаривания, L_sq - кинетическая индуктивность квадрата сверхпроводящей пленки, из которой сделан детектор. Зная выражение (2), можно связать коэффициент v с экспериментально измеряемыми параметрами пленки через формулу (3).

4.    Экспериментальная часть

В данной работе нами исследовались две геометрические конфигурации детекторов (рис. 1а) в виде мостиков. Сравнение мостиков с разной геометрией показало, что раз- линия в геометрии мостика практически не влияют на уровенв темнового счета, если стабильно выдерживается ширина мостика по всей его длине. Для проведения эксперимента была собрана установка, представленная ниже (рис. 16). В процессе эксперимента образец находился в специальном макете-держателе, который был установлен внутри вакуумного чехла. Вакуумный чехол погружался внутрь сосуда Дьюара и напрямую омывался жидким гелием. Далее жидкий гелий через капилляр, имеющийся в дне вакуумного чехла, поступал внутрь установки и охлаждал детектор до температуры в 4,2 К. Температура детектора контролировалась угольным термометром, установленным в макете. Для проведения эксперимента при температуре выше температуры кипения жидкого гелия макет был оснащен резистором - «печкой», на котором выделялось джоулево тепло, нагревающее образец. Температура детектора в процессе измерений менялась в диапазоне от 4,2 до 7,5 К.

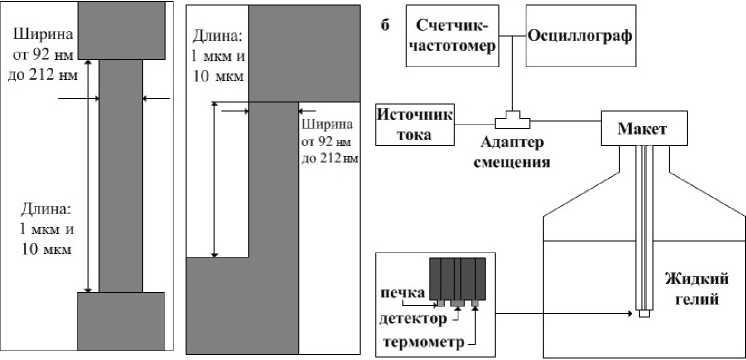
Рис. 1

5.    Результаты измерений

В результате эксперимента было получено, что уровень темнового счета детектора сильно зависит от величины тока смещения, подаваемого на образец, и достигает своего максимального значения при токах смещения, равных величине критического тока для данного детектора (рис. 2а). При увеличении рабочей температуры на 3,3 К величина критического тока детектора падала более чем в 1,5 раза с 29,4 мкА (при Т = 4,2 К) до 15,5 мкА (при Т = 7,5 К), а уровень темнового счета сокращается примерно в 28 раз с 500 кГц (при Т = 4, 2 К) до 18 кГц (при Т = 7, 5 К). График, изображенный на рис. 26, представляет пример сравнения эксперимента с теоретической моделью одиночных термически активированных вихрей для температуры 4.2 К. Наилучшее согласие между теоретической и экспериментальной кривыми получается при v ~ 85. В то же время при расчете по формулам (2) и (3) с L_sq = 100 пГн [15] и ц = 1 получается v = 65.

Из графика (рис. 26) видно, что формула (1) модели термически активированных одиночных вихрей достаточно хорошо описывает экспериментальные результаты при токах смещения, близких к критическому току образца ( Iь > 0.92/_с)- При токах смещения, меньших, чем 0,92/_с, экспериментальная и аппроксимированная теоретическая кривые начинают заметно расходиться. Это расхождение в области малых токов смещения можно объяснить несколькими причинами. Во-первых, при малых токах смещения начинают сильнее проявляться шумы. Во-вторых, при малых токах смещения прохождение термически активированных вихрей уже не является достаточным условием для образования нормальной области, а регистрируемые темновые отсчеты являются следствием другого механизма, отличного от механизма термически активированных одиночных вихрей.

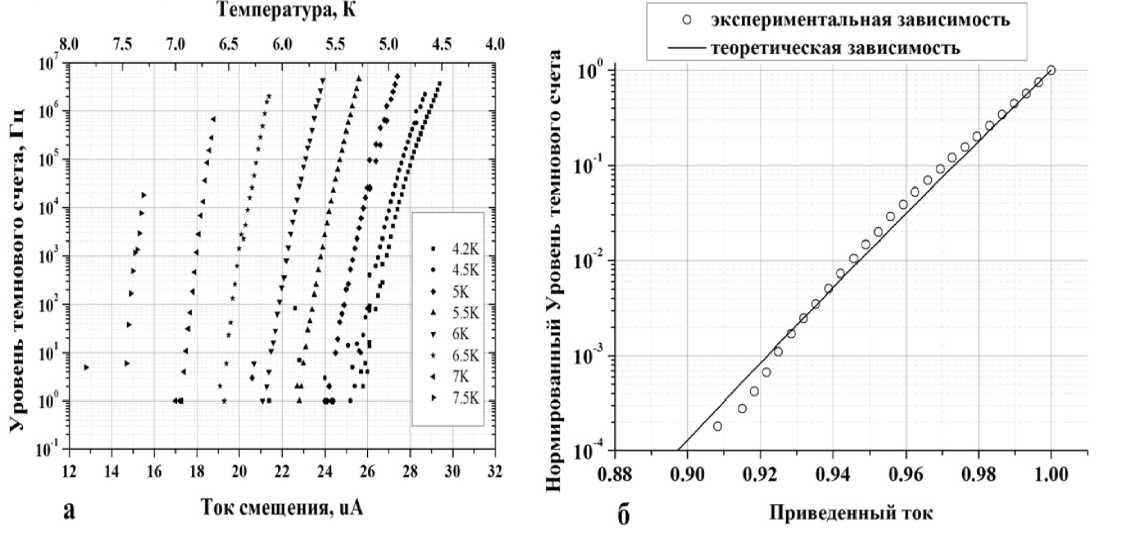
Рис. 2

6.    Заключение

Таким образом, нами обнаружено, что модель термически активированных одиночных вихрей дает достаточно хорошее количественное согласие с экспериментальными зависимостями числа темновых отсчётов SSPD в единицу времени от тока смещения детектора при больших токах смещения. Небольшое расхождение между значениями показателя v₁ рассчитанным исходя из параметров образца и полученным аппроксимацией экспериментальной зависимости, вполне может объясняться тем обстоятельством, что модель [10] основана на уравнениях Гинзбурга-Ландау, не применимых точно к описанию ситуации при Т - Т_с ~ Т_с.

Данная работа выполнена при поддержке Министерства образования и науки в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» и ФЦП «Исследования и разработки по приоритетным направлениям развития научнотехнического комплекса России» (государственные контракты № 11.519.11.3034 и № 16.523.11.3017) и Российского фонда фундаментальных исследований, грант № 12-0231841.

• *Работа доложена на 5-й Всероссийской конференции молодых ученых «Микро-, нанотехнологии и их применение» им. Ю.В. Дубровского, ИПТМ РАН, Черноголовка, 19—22 ноября 2012 года.