Исследование приведенного компетентного алгоритма над множеством алгоритмов вычисления свертки

Рассмотрим задачу вычисления свертки:

^ ( M , N ) = par ( Z ) л

M -1

y ( n ) = h ( n ) * x ( n ) = ^ h ( m ) x ( n - m ) .       (1)

m =0

А ( Z> А * ( Z ) if

u a * ( M , N ) =

и m^ л (м,N)

А : Ае^ А ?Л

A ^e             Г

•

' А ( M ’ N )

Здесь { x ( n ) } - входной сигнал, { h ( m ) } ^M0 — конеч-

ная импульсная характеристика,

{ y(n )}

N - M +1

n =0

вы-

ходной сигнал. Обозначим задачу (1) через

\ N -1 \                     г        M -1 ,

50’{ x ( n )} n=0 ) , где 5 =({ h ( n )} n=0 , ( N, 0

априорная информация о задаче.

Компетентный алгоритм

Введем функцию:

Очевидно, компетентный алгоритм для решения конкретной задачи вычисления свертки использует тот алгоритм из опорного множества, сложность которого при решении данной задачи минимальна.

Предложение 1 [1] Компетентный алгоритм А ® над множеством алгоритмов постоянной сложности { А } является алгоритмом постоянной сложности.

par Z ( ^ 0 , { x ( ⁿ ) } n =0 )

3₀=([ h(n)!M 4 N ,5- jl ⁰ ^ ^{( )}} n =0 A ’ ( x Ц/

= ( M , N ) .

Приведенный алгоритм

Определение 3 Функция сложности u_A ( M , N ) алгоритма А постоянной сложности называется корректной , если выполняется неравенство:

Определение 1 Алгоритм A называется алгоритмом постоянной сложности , если для любой задачи Z выражение для его вычислительной сложности имеет вид аналитической функции, зависящей только от величины par ( Z ) , то есть:

^V ( ^M ’ ^N ) е^К A ( M , N )

U a ( M , N ) <

uA (m,N-(M -m))

_min

Л

U ( A ( Z )) = Ua ( par ( Z ) ) = Ua ( M , N ) .

Обозначим К A ( _{M N} ) область определения алгоритма постоянной сложности .

Определение 2 Компетентным алгоритмом А ® г { А } над опорным множеством { А } алгоритмов постоянной сложности называется алгоритм вида:

< min

А ® ( M , N )

U ^К А ( M , N ) ’

^А = { A }

V Z еК

А * ( M , N )

( m , N ^{- ( M -} m ) )^еК A ( M ’ N ) , ( M ^- m , N ^- m )^еК a ₍ м _Л)

min m=0,1,2...

n =0,1,2,...

( M + m , N + m + n )^еК a ( m ’ N )

min n =1,[ N/2]

( ^M • ⁿ )^еК A ( м л) • M ,

( N - n + M -1 ) ^еК A ( MN )

u A ( M ^-^ add

m , N - m ) +   ,

ua (M + m, N + m + n )•

’

uA (M, n)(n - M +1) +

uA (M,N-n + M-1)(N-n)

N - M +1

.

Определение 4 Алгоритм постоянной сложности с корректной функцией сложности называется приведенным .

Теорема 1 [1] Для любого алгоритма постоянной сложности А , заданного на К A ( M N ) , существует (может быть сконструирован) приведенный алгоритм A : ..

A ( M , N )        A ( M , N ) ’

^V ( M , N ) GK a ( M , N ) U A ( M , N ) < U A ( M , N ) .

Теорема 2 [1] Пусть { А } - множество алгоритмов постоянной сложности, из которых построено множество { А } приведенных алгоритмов постоянной сложности. Пусть А ® - приведенный компетентный алгоритм над множеством { А } с областью определения К - ® , а А .® - приведенный ^A 1            ¹

компетентный алгоритм над множеством {А} с областью определения К соотношения:

,® . Тогда выполняются

^

A 2

К А® = К ■ I К А-) ,

V Z еК A - U ( А ® ( Z ) ) = U ( A ® ( Z ) ) .

Исследование приведенного компетентного алгоритма

Исследование проводилось для наиболее известных алгоритмов вычисления сверток, формирующих множество:

{ A dc , A , A _ _s , А 3 , А 4 , A gt } .                       (2)

Здесь:

• —    A dc — алгоритм прямого вычисления свертки [2] согласно формуле (1);

• -    А 2 , А 3 , А ₄ - вычисления свертки с использованием декомпозиции Кули-Тьюки по основаниям «2», «3» и «4» соответственно (используется дополнение входного сигнала нулями до степени соответствующего основания) [3];

• -    А 2 S - с декомпозицией Кули-Тьюки по основанию «2», дополнением нулями до степени «2» и секционированием [3, 4];

• -    A GT -с декомпозицией Гуда-Томаса и алгоритма Рейдера для вычисления малоточечных ДПФ (с использованием дополнения входного сигнала нулями до длины, раскладывающейся на взаимно простые сомножители) [3].

Исследование проводилось в двух направлениях.

Первое направление – это определение влияния операции приведения на вычислительную слож- ность алгоритмов быстрой свертки. В том числе на те, в которых используется секционирование входного сигнала. Результаты исследования представлены на рисунках 1 и 2 и таблице. Поскольку функция сложности и, (M, N) зависит от двух координат M и N , на рисунках представлены только «сечения» этой функции для значения M = 60 .

По результатам этого направления исследований можно сделать следующие выводы :

• -    функция сложности алгоритмов вычисления свертки на основе ДОП и с секционированием, и без секционирования не является корректной;

• -    использование операции приведения для алгоритмов вычисления свертки, основанных на ДОП с декомпозицией Кули-Тьюки по различным основаниям с секционированием сигнала и без него, позволяет уменьшить сложность решения большинства задач (50-56%) в области определения соответствующих алгоритмов (рис.1, 2);

• -    значительное снижение сложности для указанных алгоритмов происходит для задач с параметрами ( M , N ), у которых длина сигнала N чуть больше степени основания декомпозиции Кули-Тьюки (рис.1, 2). Для таких задач возможно снижение сложности более чем на порядок (показатель (2б) в таблице).

  

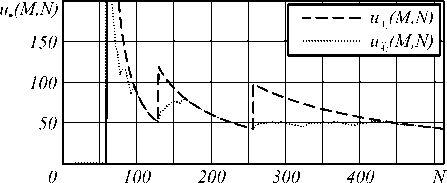
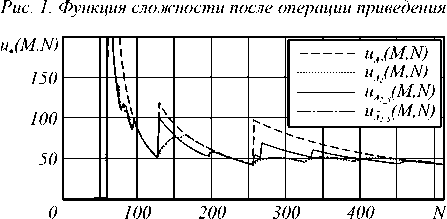
Рис. 2. Функция сложности после операции приведения для алгоритма с секционированием

Вторым направлением является исследование приведенного компетентного алгоритма. Для этого из указанного в (2) множества алгоритмов постоянной сложности выбиралось некоторое подмножество Α , называемое опорным. Сложность каждого алгоритма опорного множества определялась на области К(MN) =[1,512] х [1,512]. Над опорным подмножеством Α строился компетентный алгоритм А®. Для него выполнялась операция приведения, результатом которой являлся приведенный компетентный алгоритм А®. На рисунках 3-5 (по мере увеличения числа алгоритмов опорного множества) приведены функции сложности для алгоритмов опорного множества и построенного над ними приведенного компетентного алгоритма.

По представленным результатам можно сделать следующие выводы :

• -    независимо от числа алгоритмов опорного множества, можно рассчитывать на снижение сложности в относительно большом (более 30%) числе отсчетов области определения;

• -    для отсчетов области определения, в которых произошли изменения функции сложности в результате операции приведения, можно рассчитывать на снижение сложности в среднем на 1030% (от сложности компетентного алгоритма).

• -    как число отсчетов области определения, в которых операция приведения снижает сложность компетентного алгоритма, так и собственно величина этого снижения зависит не только (а с учетом представленных результатов, не столько) от числа алгоритмов опорного множества, а в значительной степени от вида функции сложности этих алгоритмов. То есть, в общем случае нет монотонного поведения ни одного показателя от числа алгоритмов опорного множества (таблица), кроме средней сложности итогового алгоритма A ® ;

  - по мере наращивания мощности опорного множества алгоритмов, величина снижения средней сложности и компетентного, и приведенного компетентного алгоритма оказывается все меньше (см. поведение показателей (5) и (6) в таблице). В частности, при переходе от трех к пяти алгоритмам в опорном множестве показатель (6) снижается всего на 10% (с 113 до 102 операций) по сравнению с почти 30% снижения (со 165 до 117) при переходе от одного алгоритма к двум. Поэтому на практике представляется малоэффективным процесс бесконечного наращивания мощности опорного множества алгоритмов. Практически тех же результатов (по сложности решения задач свертки) можно добиться и при сравнительно малом количестве алгоритмов. По

той же причине, и процесс синтеза новых алгоритмов вычисления сверток, которые по показателю сложности не превосходят радикально существующие , с практической точки зрения является нецелесообразным.

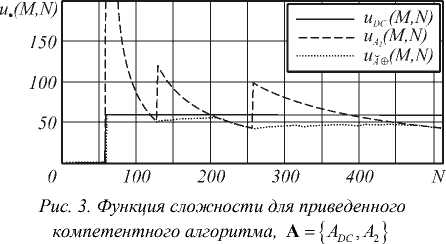
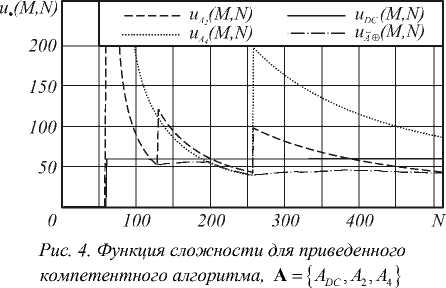
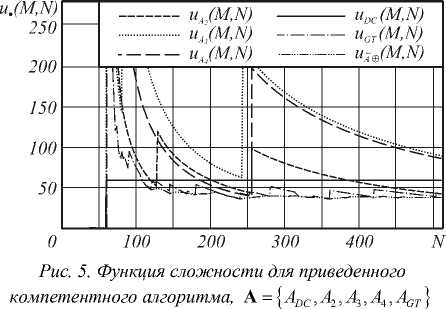
Таблица 1. Сводные характеристики изменения сложности алгоритмов решения задачи Z при использовании операции приведения

Показатель	Алгоритм
	A 2_ S	A 2	{ A DC , A Г	Гл л 1@ DC , 2 , 1 A 4      J	® 1 A DC , A 2 , A 3 , 1 1 A 4 , A GT    J
(1) относительное число отсчетов области определения, в которых произошло снижение сложности алгоритма	0.499	0.563	0.348	0.394	0.423
(2а) максимальное абсолютное уменьшение сложности алгоритма	17863	17863	77.717	88.478	91.944
(2б) максимальное относительное уменьшение сложности алгоритма	12.102	12.603	1.929	2.132	1.323

(3а) среднее абсолютное уменьшение сложности алгоритма, нормированное на количество отсчетов, в которых произошло изменение сложности	271.070	250.367	24.353	29.870	10.932
(3б) среднее относительное уменьшение сложности алгоритма, нормированное на количество отсчетов, в которых произошло изменение сложности	1.405	1.650	1.220	1.274	1.104
(4а) среднее абсолютное уменьшение сложности алгоритма, нормированное на мощность области определения	135.160	140.902	8.4693	11.754	4.620
(4б) среднее относительное уменьшение сложности алгоритма, нормированное на мощность области определения	0.701	0.928	0.424	0.501	0.466
(5) средняя сложность компетентного алгоритма	299.505	306.115	125.414	124.831	106.618
(6) средняя сложность приведенного алгоритма	164.346	165.213	116.944	113.0767	101.998

а)

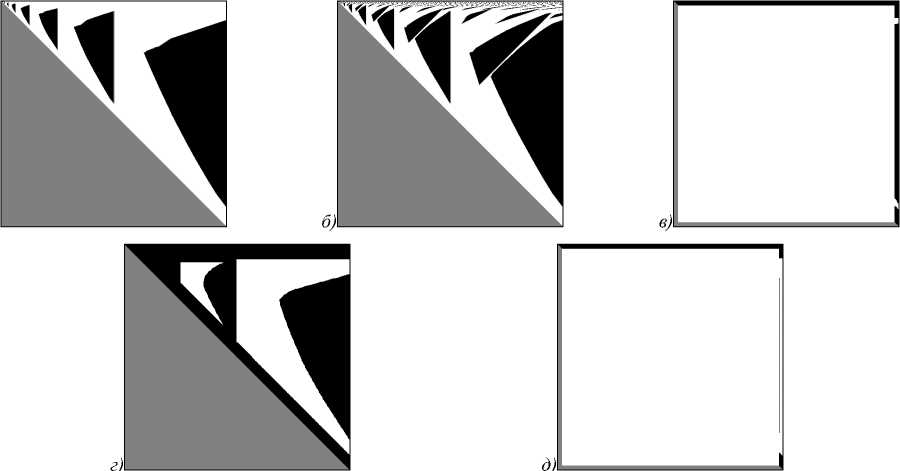
Рис. 6. Отсчеты области определения, в которых операция приведения снизила сложность соответствующего алгоритма решения задачи вычисления свертки: (серым - отсчеты, не входящие в область определения, белым - отсчеты области определения, в которых операция приведения снизила сложность соответствующего алгоритма, черным - отсчеты области определения, в которых операция приведения не изменила сложность соответствующего алгоритма) а) A 2 ; б) A 2_ _s ; в) { A _DC , A 2 } ' ; г) { A _DC , A 2 , A 4 } ' ; д) { A _DC , A 2 , A 3 , A 4 , A } '

Работа выполнена при поддержке:

• •    РФФИ (проекты № 06-01-00616-а, № 07-07-97610-р_офи);

• •    Фонда содействия отечественной науке;

• •    российско-американской программы «Фундаментальные исследования и высшее образование» (CRDF Project RUX0-014-SA-06).