Исследование процесса конвективной сушки нетканых материалов

Процесс сушки характеризуется сложными закономерностями переноса тепла и влаги как внутри влажного тела, так и при взаимодействии поверхности материала с окружающей средой. Поэтому при описании кинетики сушки широко используются экспериментальные зависимости, основанные на наиболее общих закономерностях процесса.

Длительность сушки – важнейший параметр процесса, определяющий качество высушиваемого материала. Для практики сушки актуальной задачей является использование экспериментальных зависимостей с минимальным количеством констант, определяемых из опыта, что значительно упрощает исследование кинетики сушки, и отпадает необходимость проведения трудоемких и сложных экспериментов.

Представляется важным установить точность и границы использования данного метода для расчета кинетики процесса и времени сушки.

К таким методам относятся метод А.В. Лыкова [1], метод Р.В. Красникова [2], метод Н.Ф. Докучаева и М.С. Смирнова [3].

Докучаев и Смирнов [3, 4], применив уравнение фильтрации пара через пористую структуру влажного материала, получили уравнение кривой сушки в виде:

W = W0

т

b + Kt

,%,

где b и К - коэффициенты, зависящие от режима сушки и рода материала.

Параметры b и К , по данным авторов метода, могут быть определены с известным приближением без проведения длительных опытов по 2-3 экспериментальным точкам, используя соотношения:

И

М 0

;

b = —T—, w0 - W1

где T I - время, близкое к начальному, мин; W 1 - соответствующее ему влагосодержание, %; W 0 - начальное влагосодержание, %;

Дифференцируя соотношение (1), получим уравнение кривой скорости сушки.

dW

dT

b

----------, % / мин .

( b + K t )²

Продолжительность процесса сушки влажного материала до заданного влагосодержания W определяется из уравнения (1)

т =

b(W0 - W)1 - К(W0 - W)

, мин ,

где W - текущее значение влагосодержания, %.

Для использования метода Докучаева-Смирнова в инженерной практике необходимо установить закономерности изменения коэффициента b в периоде падающей скорости сушки.

Однако обработка и анализ опытных данных по сушке различных материалов показали, что коэффициент b уравнения (1) не является постоянной величиной, а зависит от режима сушки и влагосодержания тела. В периоде убывающей скорости сушки коэффициент b непрерывно изменяется по определенным закономерностям, которые устанавливаются режимом сушки.

Проведем анализ процесса сушки на основе метода Докучаева-Смирнова [4]. В практике сушки широкое использование получило понятие обобщенного времени N t , названное обобщенным временем сушки, где N - скорость сушки в первом периоде.

Величина N T является устойчивым комплексом величин, характерных для процесса сушки. Комплекс N t позволяет построить обобщенную кривую сушки для различных режимов при начальном влагосодержании W ₀ . Изучение процесса сушки на основе N Т позволяет рассматривать не частный случай, а множество различных случаев сушки, объединенных общностью режимных параметров процесса.

Для определения скорости и времени сушки необходимо знать закономерности изменения параметра b в периоде падающей скорости.

На рис. 1 а представлена зависимость коэффициента b в полулогарифмических координатах от обобщенного времени N Т при конвективной сушке войлока для различных режимов.

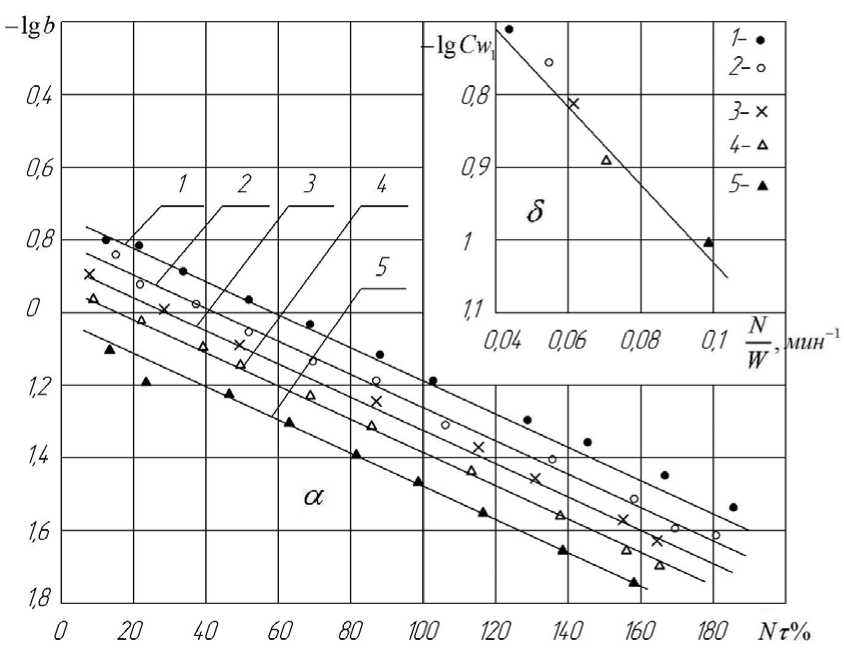
Рисунок 1 – Зависимость коэффициента b уравнения 1 от обобщенного времени сушки Nt (а) и коэффициента CW1 от отношения N (б) в процессе конвективной W сушки войлока при режимах сушки:

1 - t c = 90 0 C , и = 5 м/с; 2 - t c = 120 0 C , и = 3 м/с;

3 - t c = 120 0 C , и = 5 м/с; 4 - t c = 120 0 C ; и = 10 м/с; 5 - t c = 150 0 C , и = 5 м/с

Семейство, изображенных прямых, описывается уравнением

b = CW 1exp (-0,01 N т).

Коэффициент C_{W 1} , учитывающий влияние режима сушки (рис. 1 б), вычисляется по соотношению

С

W 1

0,27exp

-9,87

W

Наибольшее влияние на коэффициент b оказывает величина максимальной скорости сушки материала N в первом периоде, которая зависит от режима сушки (температуры теплоносителя t c и скорости и ).

Следовательно, скорость сушки N также можно считать некоторой обобщенной переменной, в которой отражено влияние всех режимов сушки, воздействующих на процесс.

Для более полного и детального изучения влияния отдельных параметров режима сушки на величину коэффициента b уравнения (1) обработка опытных данных была проведена в виде зависимости b =

Г W 0 - W

I N ,

, приведенной на

рис. 2 (а). При таком способе обработки опытных данных также получено семейство прямых, где влияние режима сушки отражено величиной N .

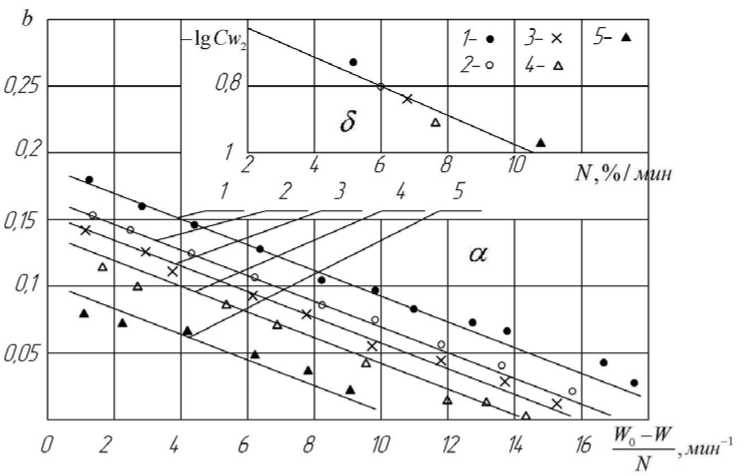
Рисунок 2 – Зависимость коэффициента b в уравнении 1 от комплекса   ⁰ N   (а)

и коэффициента C W2 от параметра N (б) в процессе сушки войлока. Режимы сушки указаны на рисунке 1

Представленную на рис. 2 а, б зависимость можно записать в виде

, И -И b = Cw 2 - 9,4 • 10-3 0 N   ,

CW 2 = 0,3exp (-0,084N ).

При обработке экспериментальных данных по сушке влажных материалов разными способами энергоподвода использовалась зависимость [5, 6]

• 1    dW

N = Ndk = CXP (" aNT) ’ где N* – относительная скорость сушки.

Коэффициент a зависит только от критического влагосодержания W_кр и для целой группы материалов определяется соотношением [5, 6]

a =

0,8

W

Wкр

’ 1 / %.

Из выражений (3) и (9) для скорости сушки можно записать

b

( b + K т) 2

N exp (-aN т).

Уравнение (11) запишем в виде

b + K т _       1

4b   у N exp (-aNт)

На рис. 3 дано графическое изображение уравнения (12), где для удобства левая и правая часть уравнения обозначены через В и А .

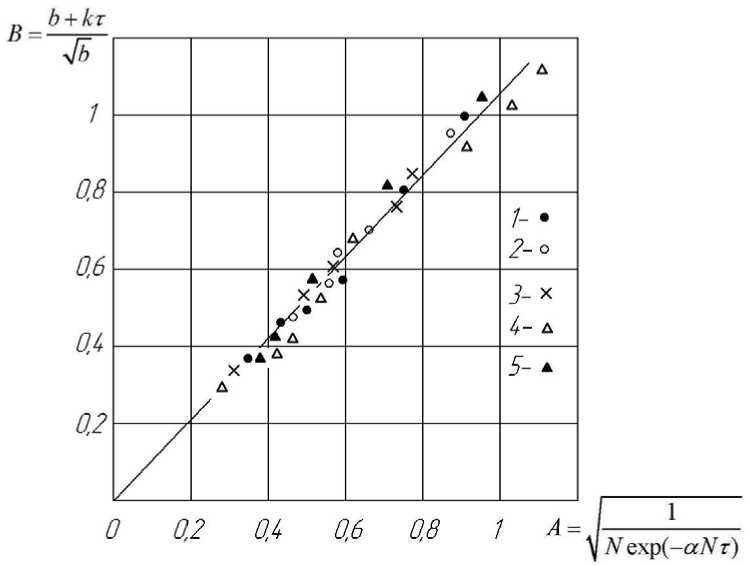
Рисунок 3 – Зависимость между параметрами В и А уравнения (12) для войлочной пластины в процессе конвективной сушки. Режимы сушки указаны на рисунке 1

При решении уравнения (12) коэффициент b определялся экспериментом, а коэффициент К – по соотношению (2).

Уравнение (12) (рис. 3) является тождеством ( В = А ). На основе графического изображения уравнения (12) и обработки опытных данных по сушке войлока получена зависимость (рис. 4 а, б)

b _----1     ;

Cw з A - 6

C _ 571N.

W 3 W ₀

Для вычисления коэффициента b можно также воспользоваться соотношением где

b = Cw 4exp(-2,8 A ).

Cw 4 = 1,85exp(-25 N / W0),

A =

\ N exp( - aNT )

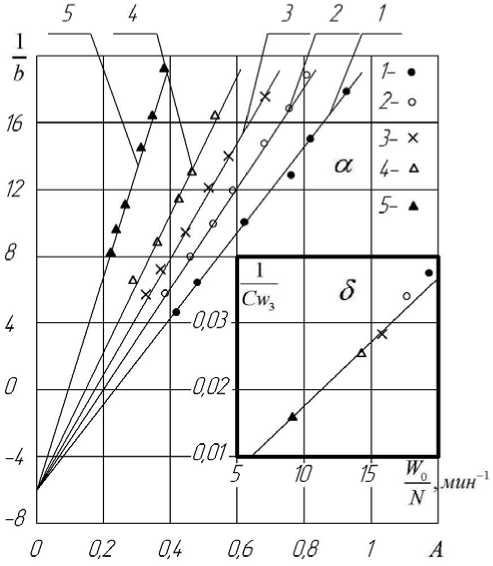
Рисунок 4 – Зависимость коэффициента 1 / b от параметра

A =

N exp( - aNT),

• (а) и коэффициента от отношения ⁰ (б) для войлочной пластины в

CW 3             N процессе сушки. Режимы сушки указаны на рисунке 1

Таким образом, исследование процесса сушки войлока показало, что изменение коэффициента b для периода убывающей скорости сушки происходит по закономерностям, в которых основное влияние на эти изменения оказывает максимальная скорость сушки N и влагосодержание материала W .

В процессе сушки подошвенной кожи и других влажных материалов [5] для определения средней температуры тела в периоде убывающей скорости сушки использовалась формула, относящаяся к классу дробно-рациональных функций:

t C = 1 ₀ +

T

a ₀ + a 1 T

,       ,

где t - среднеинтегральная температура влажного тела в момент времени т ; а ₀ и a ₁ – параметры, зависящие от температуры и влагосодержания материала.

Сравнение формул (1) и (17) показывает их полную идентичность, а коэффициенты, входящие в эти уравнения, вычисляются по аналогичным соотношениям. Средняя температура материала t ₀ в первом периоде зависит только от температуры среды t _c ^:

/ = 10 + 0,28t .

0                   ⁷ c

Параметр а 1 уравнения (17) вычисляется по соотношению, аналогичному выражению для определения коэффициента К уравнения (1):

a 1 =

1tc - t0

Коэффициент a0 уравнения (1) определяется совместной обработкой кривых сушки W = f (т) и температурных кривых t = f (т) для периода убывающей скорости сушки.

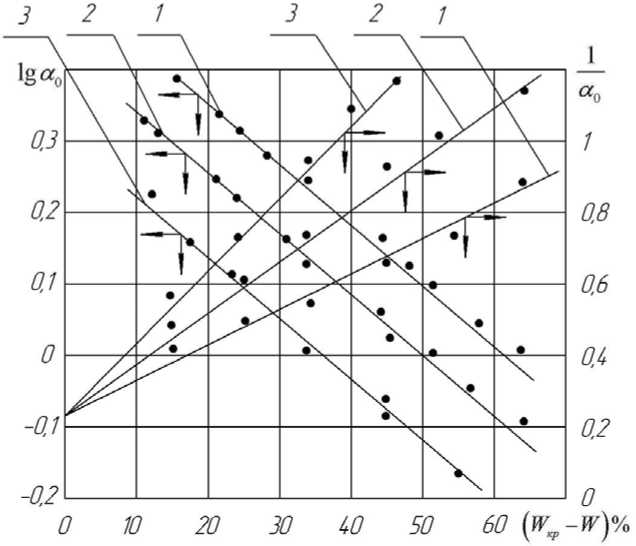
Рисунок 5 - Зависимость коэффициента lg а ₀ и 1/ a 0 уравнения (17) от влагосодержания ( W - W ) при сушке войлока. Режимы сушки: 1 — 90 0 C , и = 5 м/с; 2 - t c = 120 0 C , и = 3 м/с; 3 - t c = 150 0 C , и = 5 м/с;

На рис. 5 представлены зависимости lg а ₀ = f (W_Kp

- W ) и — = f (W - W ) , a 0

которые выражаются уравнениями

a0 = Ct6pexp((-0,017(W - W));

a ° C4W - W ) + 0,25;

где коэффициенты C t 1 и C t ₂ определяются по соотношениям

Ct 1 = 5,4 - °,°23 tc;

Ct2 = (°,13tc - 2) • 1°-3.                                (23)

Сопоставляя все графики и формулы для коэффициентов b и a ° в уравнениях (1) и (17), можно отметить, что построение графиков и вывод формул для вычисления этих коэффициентов проводится по единой методике обработки экспериментальных данных.

Единая методика обработки экспериментальных данных при построении графиков и вывода расчетных уравнений для вычисления коэффициентов b и a ° позволяет использовать метод Докучаева-Смирнова для расчета и влаго- и теплообмена в периоде убывающей скорости сушки.

Основное уравнение кинетики сушки А.В. Лыкова [1]

q * = q IL = n *(1 ₊ Rb ), q _I

где    q I q II - плотности теплового потока в первом и втором периодах, Вт/м²;

q * - относительный тепловой поток; Rb - число Ребиндера.

Плотность потока тепла в первом периоде

„ N „ ,2 q_r = p rR —, Вт/м , ¹  ^° ^v 1°°

где р ° - плотность сухого тела, кг/м³; r - теплота парообразования, кДж/кг;

R_V – отношение объема тела к поверхности, м.

Критерий Ребиндера определяется эмпирической формулой [1]

Rb = A exp(-n(u - up)),

где влагосодержание материала u = °,°1 W , и_р - равновесное влагосодержание материала. Постоянные А и n в формуле (27) для нетканых материалов даны в таблице 1.

Таблица 1 – Постоянные А и n для войлока и фетра

Материал	Режим сушки			А	n
	t c , 0C	υ , м/c	φ , %
Войлок 3 = 8 - 18 мм	90-150	3-10	5	0,1	6
Фетр 3 = 4 мм	50	0,5-0,7	24-74	0,1	10

Относительный тепловой поток q * во втором периоде изменяется по экспоненциальному закону и для влажных плоских материалов при конвективной сушке, если кривые скорости сушки относятся к типу 3 по классификации А.В. Лыкова [1] и обращены выпуклостью к оси влагосодержания, определяется выражением

q * = 0,83exp(-0,12т), (27)

где т - время сушки во втором периоде, отсчитываемое от т = 0 . В таблицах 2 и 3 дано сравнение экспериментальных и расчетных значений коэффициентов b и а ₀ , времени сушки и среднеинтегральных температур для процесса сушки войлочной пластины по приведенным уравнениям. Совпадение опытных и расчетных значений находится в пределах точности эксперимента.

Таблица 2 – Сравнение экспериментальных и расчетных значений коэффициента b и времени сушки τ по уравнению (4) для конвективной сушки войлока при режиме: t c = 120 0 C , и = 3 м/c; ф = 5 м/с

W , %	b экс	τ экс . мин	b(5)	t р (4), мин	b(7)	t р (4), мин	b(13)	t р (4), мин	b(15)	t р (4), мин
100	0,145	2,5	0,138	2,38	0,15	2,59	0,134	2,3	0,14	2,4
90	0,125	4	0,124	3,96	0,14	4,45	0,122	3,9	0,13	4,15
60	0,09	9,5	0,088	9,43	0,094	9,9	0,089	9,4	0,1	10,4
40	0,07	15	0,065	15,1	0,065	14,2	0,068	14,7	0,071	15,3
20	0,041	22,5	0,0395	21,6	0,035	21,6	0,047	23,1	0,041	22,5
10	0,024	30,5	0,027	32	0,022	28	0,03	35	0,021	27

Таблица 3 – Сравнение экспериментальных и расчетных значений коэффициента а0 и среднеинтегральных температур t по уравнению (17) для конвективной сушки войлока при режиме: tc = 120 0C, и = 3 м/с; ф = 5 м/с,

W кр = 75 %

W , %	а0 экс	tc0	а 0рас (20)	t рас (17) 0С	а 0рас (21)	t рас (17) 0С
60	2,13	47	2,06	47,4	2,18	47,1
50	1,75	49	1,73	49,4	1,695	49,5
40	1,34	52	1,42	52,2	1,37	52,6
30	1,09	55	1,2	55,6	1,15	56
20	1,02	59	1,04	59,9	1	60,3
10	0,9	64,5	0,88	65,8	0,88	65,7

ВЫВОДЫ

Исследование кинетики сушки на основе метода Докучаева-Смирнова, проведенное авторами, позволило установить условия использования данного метода для расчета влаготеплообмена в периоде падающей скорости сушки без проведения длительных экспериментов при заданном начальном влагосодержании материала, не прибегая к вычислению коэффициентов теплообмена. При использовании метода достаточно знать только первое критическое влагосодержание материала Wкр, которое незначительно изменяется при изменении режима сушки, и скорость сушки в первом периоде N, которую в первом приближении можно определить по 2-3 экспериментальным точкам для заданного режима сушки.