Исследование процесса перемещения внутренней емкости автобалансирующего устройства с вытесняемой жидкостью стиральных машин

Одним из наиболее перспективных способов снижения виброактивности стиральных машин с горизонтальной осью вращения является использование жидкостных автобалансирующих устройств (АБУ) пассивного типа. Обоснованность данного вывода связана, в первую очередь, с появлением новых схем и технологий использования свойств жидкостных АБУ, позволяющих при незначительных затратах наих модернизацию повысить эффективность борьбы с вибрацией в стиральных машинах при центробежном отжиме.

В настоящее время одними из таких перспективных АБУ являются устройства, в которых уравновешивающие массы формируются за счёт рабочей жидкости, заполняющей без пустот межстенную герметичную полость и вытесняемую внутренней ёмкостью с упругими связями, к которой приложена центробежная сила от неуравновешенных масс текстильных изделий, в область противоположную направлению действия этой силы (так называемые, жидкостные АБУ с вытесняемой жидкостью) [1], [2].

Однако, жидкостные АБУ с таким принципом действия до настоящего времени не нашли широкого применения в стиральных машинах, что связано, главным образом, с практически отсутствием результатов научных исследований данных устройств и обоснованных рекомендаций по выбору их рациональных параметров, обеспечивающих эффективность снижения виброактивности при отжиме.

Для решения поставленных задач проведем анализ процесса перемещения внутренней емкости АБУ при действии на нее неурав-F смещения внутренней ёмкости при силовом

F вдоль оси OZ от неуравновешенных масс текстильных изделий (белья) m g в период центробежного отжима.

В результате действия на внутреннюю емкость силы F,б-тб^в ге.б, где m^ - масса текстильных изделий (белья), кг; соБ - частота вращения барабана при отжиме, рад/с; ге.б -эксцентриситет неуравновешенных масс текстильных изделий, м, происходит её смещение относительно оси вращения барабана на вели-l нительной неуравновешенной силы F4..

F. _e- m₆to _Bk 1 ,

где m_e - масса внутренней ёмкости, кг; /1 1 - смещение внутренней ёмкости под действием силы F₄.6 вдоль оси OZ (другими словами, эксцентриситет массы внутренней ёмкости относительно оси вращения барабана), м.

При этом эксцентриситет ге.б центра масс отжимаемых текстильных изделий увели-l сила F4.6 от неуравновешенных масс отжимаемых текстильных изделий с учётом эксцентриситета (ге. б+А 1) будет определяться зависимо стью:

F ₆- m^² ( г_е. ₆+Д 1 ).                  (2)

Таким образом, при смещении внутренней ёмкости формируется суммарное усилие (центробежная сила F₄ от неуравновешенных масс барабана) F₄-F^. _s+ F^ направленное вдоль линии действия центробежной силы F₄.₆ и воздействующее таким образом через упругие элементы АБУ на её внешний каркас и, соответственно, на подвесную часть стиральной машины в виде динамической нагрузки:

F -со_Б² [ m_eM + m₆ ( г .б+Д 1 )],           (3)

или

F -CDs² [ m₆r_e,₆ + ( m₆ + m₆ )Д 1 ].           (4)

Силовому воздействию силы F^ на внутреннюю ёмкость оказывается упругое со- противление со стороны упругих элементов АБУ в виде силы F„:

Fyn=^1-с,

где с - жёсткость упругих элементов АБУ в направлении действия силы F₄.₆ вдоль оси OZ, Н/м.

Так как в рассматриваемой системе выполняется условие:

F - F_y „, то в соответствии с (4) и (5) будем иметь: со_Б ² [ m₆r_e,₆ + ( m₆ + m_e )Д 1 ]-Д 1 • п .

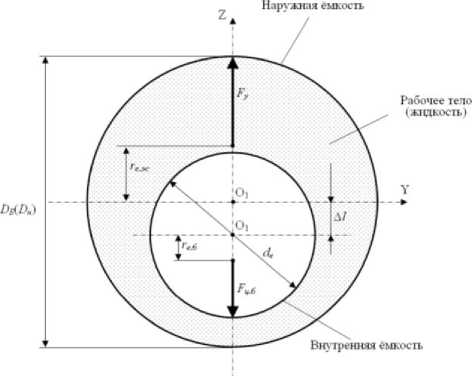
Рисунок 1 - Схема смещения внутренней ёмкости: D_B ( D_H.) - диаметр барабана (диаметр наружной ёмкости), d_e,₆ - диаметр внутренней ёмкости; г^ - эксцентриситет центра масс кольца рабочей жидкости; A 1 - силовое смещение внутренней ёмкости; F₄ - внешнее силовое воздействие в виде центробежной силы от неуравновешенных масс текстильных изделий (белья) m g в период центробежного отжима; F_y - уравновешивающая сила

Откуда перемещение внутренней ёмкости при воздействии на неё силы F₄ будет определяться зависимостью:

l

mr^

( . ^m 6 ^{+ m} J О Б

Полученная формула (8) соответствует тем решениям, которые ранее были получены при рассмотрении задач подобного типа. В частности в книге [3] приводится аналогичное решение при рассмотрении движения тела с упругой связью вдоль стержня, вращающегося вокруг оси.

Отметим, что функция (8) имеет смысл при c-(m₆ + m _e)02 >0. То есть, система упругих элементов АБУ будет адекватно реагировать на входное силовое воздействие и выполнять свои функции при условии:

о( m+m) 02,                ⁽⁹⁾

где, обозначив неуравновешенную  массу

(m₆+m _e) вращающегося барабана через m_B ,

получим

^С>\ m 5®²J . (10)

Определим возможные диапазоны жёсткости с упругих элементов АБУ. Зададимся значениями входящих в правую часть неравенства (9) параметров. Значения загрузки машины примем исходя из наиболее применяемых величин: m0=5...6 кг (в соответствии с конструктивными особенностями стиральных машин). Текущие значения массы отжимаемых текстильных изделий mб и эксцентриситет rе.б, изменяющихся в течение процесса центробежного отжима, будем определять в соответствии с методикой, приведённой в диссертации Фети сова ИВ. [4]. Для этого примем частоту вращения барабана при установившемся процессе отжима n№ст=Ю00 МИН -1 ( Юд;с„,=104,72 рад/с). Масса mв внутренней ёмкости (в машинах без АБУ - барабана mб) обычно находится в пределах mв=mб=1,0...2,0 кг, примем mв=mб=1,5 кг.

Для принятых диапазонов параметров правой части неравенства (9) определим интервал её значений. Графики значений выражения (m 2 mб и(й_б приведены на рис.2 и 3.

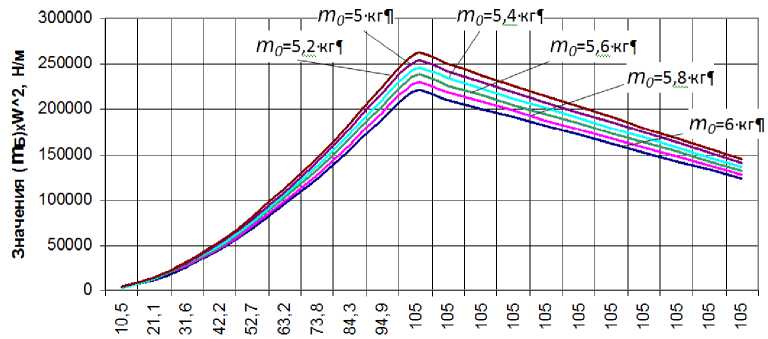
частота вращения w, рад/с

отю_в при различных величинах m _б (для оценки неравенства (9)

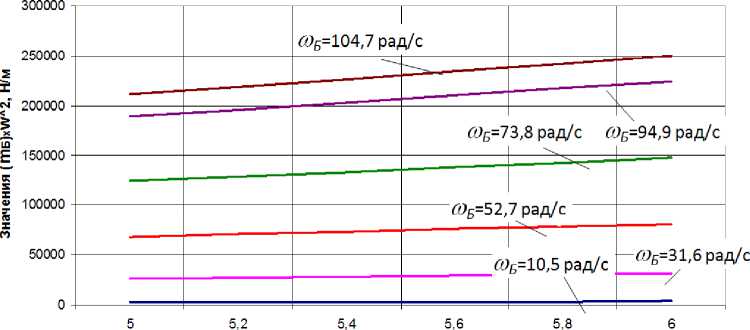
масса изделий тб, кг

Рисунок 3 - Графики значении выражения ( mдОд 1 в зависимости от mб при различных величинах юБ (для оценки неравенства (9)

Как показывают полученные данные, для принятых значений конструктивных и режимных параметров стиральной машины мак-2\ симальные значения выражения I m дОд) соответствуют моменту начала установившегося вращения барабана при ro5_VC„;= 104,72 рад/с и находятся в пределах от 220454,2 Н/м (для m =5

кг) и 261255,2 Н/м (для m б=6 кг), причём значо

(m 5® ²з

ния

растут пропорционально росту массы mб отжимаемых текстильных изделий.

Полученные данные позволяют сделать вывод, что для принятых диапазонов значений конструктивных и режимных параметров стиральной машины должно выполняться условие:

0(220454,2...261255,2) Н/м         (11)

в зависимости от массы текстильных изделий тб .

Рассчитаем, используя формулу (8), значения перемещений A l для диапазона жёсткости с=( 100000... 1100000) Н/м.

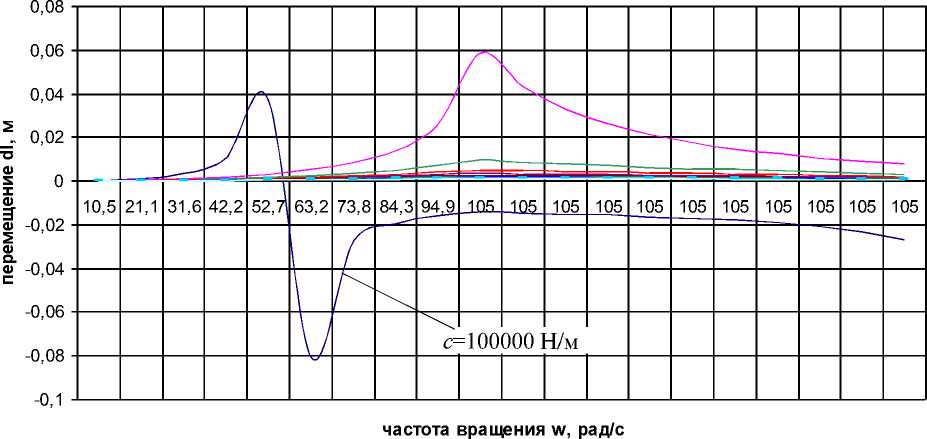
Графики зависимости Al=f(а)Б) приведены на рис.4. Причём, с учётом того, что для всех значений принятого диапазона загрузки машины т0=5... 6 кг отрицательные значения Al наблюдаются на всех графиках при жёсткости с=100000 Н/м (что соответствует условию неравенства (11)), то есть силы упругости Fyn упругих элементов АБУ меньше приложенной

F два графика - при т о=5 к г и т о=6 кг - так как качественное поведение остальных графиков при то=5,2; 5,4; 5,6 и 5,8 кг аналогично.

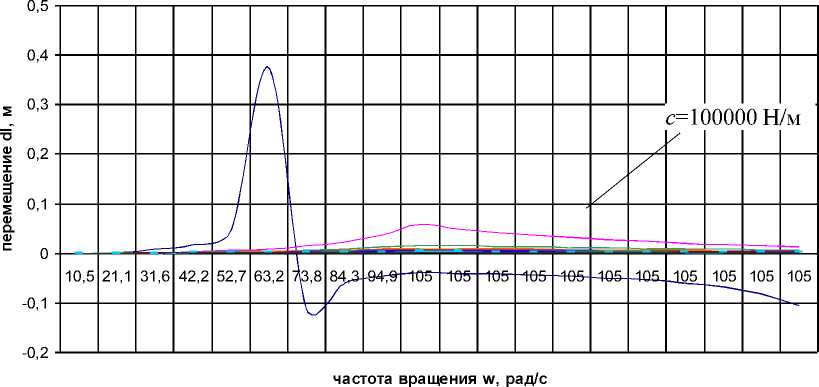
а) при т о=5 кг

б) при т о=6 кг

Рисунок 4 - Графики функции A l = f (со^) (для диапазона с= 100000... 1000000 Н/м)

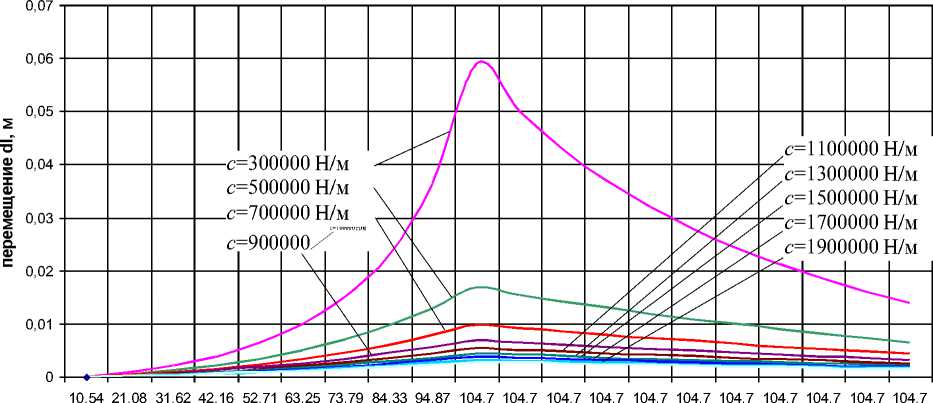
Для дальнейшего анализа полученных графиков исследуемой функции Al=f(Юб) не будем учитывать значения перемещений Al при жёсткости с=100000 Н/м (так как, как было указано выше, при этом не выполняется условие (11), то есть такая жёсткость недостаточна для создания адекватного упругого сопротивления упругих элементов АБУ центробежной силе F4, приложенной к внутренней ёмкости АБУ). Полученные графики представлены на рис.5.

Анализ полученных данных показывает, что функция Al=f(соБ) имеет локальный максимум, соответствующий началу установившегося режима вращения барабана при часто-тео)Б=104,72 рад/с и обусловленный режимными особенностями протекания процесса отжи- ма. Здесь рост значений Аl на левой ветви кривой графиков обусловлен ростом частоты вращения барабана при его разгоне отсо^О до ®Буст- Ю4,72 рад/с, а соответственно и ростом центробежной силы FX.

Последующее снижение значений Аl на правой ветви кривой графиков обусловлено снижением центробежной силы Fч, что вызвано снижением массы отжимаемых текстильных изделий mб.

Аналогичное поведение функции возмущающей силы F , = f (со_Б) показано в диссертации Фетисова ИВ. [4], что говорит о достоверности полученных результатов исследования функции А l = f ( (Й_Б ).

частота вращения w, рад/с

частота вращения w, рад/с

б) при m 0=6 кг

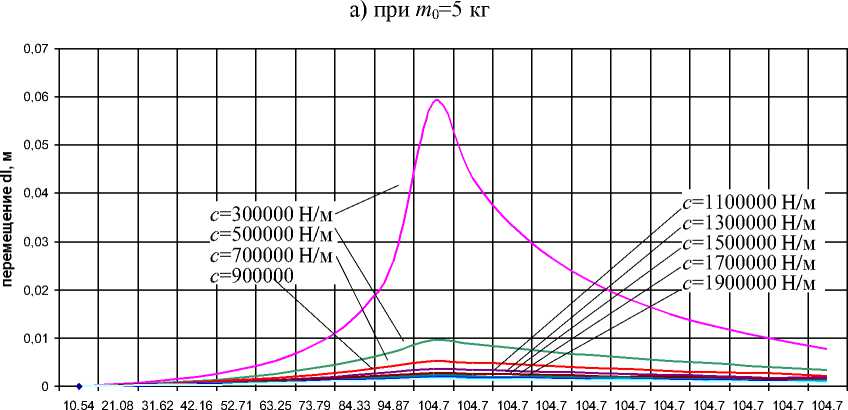
Рисунок 5 -Графики функции А l = f (со_Б) (для диапазона с=300000... 1000000 Н/м)

Рассмотрим изменение величины перемещения Аl в зависимости от жёсткости с упругих элементов АБУ. Анализ графиков на рис.5 показывает, что поведение функции Аl=f(с) для одного и того же периода времени отжима носит качественно одинаковый характер при различных значениях жёсткости с. Таким образом, достаточно рассмотреть поведение функции Аl=f(с) для одного периода времени отжима, в качестве которого примем время отжима, соответствующее максимальному перемещению А lmax подвесной части, что соответствует, как было показано выше, началу установившегося вращения барабана при установившейся частоте ®Буст (в данном СЛ\ЧаС ЭТО ®Буст=104,72 рад/с).

На рис. 6 показан график зависимости А l max= f (с) при со_Бге„,=1О4,72 рад/с.

0,08
0,07
5
■О 0,05 ф ф				m0 =5
0 04 ф ф 0 03				0    , / m0 =5,4
Q- 0,03 Ф С				m0 =5,6 m =5 8
0,02					0 =6
0,01 0						"      - =

300000 500000 700000 900000 1100000 1300000 1500000 1700000 1900000

Жёсткость с, Н/м

Рисунок 6 -Зависимость А l max= f ( с )

Полученные результаты показывают, что в данном случае перемещение А l является нелинейной функцией жёсткости с (как это очевидно и из формулы (8)), хотя, как известно, в традиционных упругих системах наблюдается линейная связь между приращением (или сокращением) А l длины упругого элемента и его

Предложенный в данной работе научный подход к определению перемещения внутренней ёмкости АБУ и полученные математические зависимости позволяют более детально исследовать процесс формирования уравновешивающих масс и сил в АБУ с вытесняемой жидкостью.

F жесткостью с : l

.

c

Такой «парадокс» объясняется тем, что для линейной зависимости А l max= f (с) необходимо, чтобы и приложенная сила F носила также линейный характер. Вместе с тем, в упругой системе АБУ происходит процесс формирования перемещений А l внутренней ёмкости под действием силы F при котором изменение жёсткости с ведёт изначально к линейному изменению перемещения А l , которое, в свою очередь, в соответствии с формулой (4) определяет приложенную нагрузку в виде силы F₀ которая, также в свою очередь, определяет величину перемещения А l , что в итоге формирует нелинейную зависимость А l max= f ( с ).

Анализ функции А l max= f (с) также указывает на то, что в принятом диапазоне жёсткости с=300000... 1000000 Н/м (для принятых конструктивных и режимных параметров стиральной машины, кроме с=100000 Н/м) упругих элементов АБУ были получены приемлемые значения перемещения Аl внутренней ёмкости, не превышающие 0,07 м, реализация которых вполне возможна в реальных стиральных машинах барабанного типа.