Исследование процесса прокатки высокой полосы с малыми обжатиями

Большинство из существующих в настоящее время зависимостей для определения усилия прокатки выведены из предположения о том, что пластическая деформация проникает на всю глубину деформируемой полосы в геометрическом очаге деформации. В то же время на практике применяются процессы прокатки с малыми обжатиями (например, обжатие кромок полосы при производстве толстых листов), когда это условие не соблюдается.

Наиболее подходящим методом определения усилия, в данном случае, является метод линий скольжения [1]. Данный метод применяется для решения плоских и осесимметричных задач. Однако он имеет свои недостатки, один из которых заключается в неоднозначности построения сетки линий скольжения.

Поэтому для построения достоверной математической модели процесса прокатки высокой полосы с малыми обжатиями проведено экспериментальное исследование по определению фактической формы очага деформации.

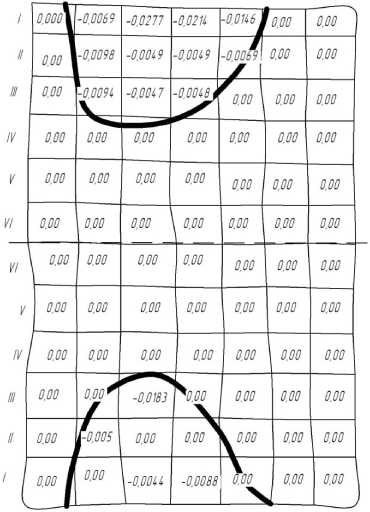
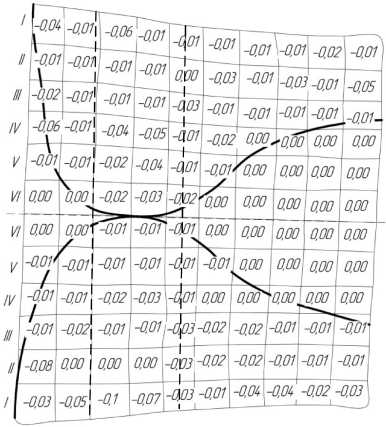
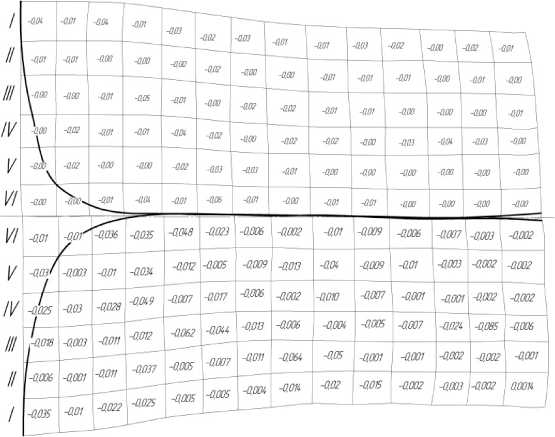
Для изучения характера пластической деформации в эксперименте использовались свинцовые заготовки с нанесенной на боковую поверхность координатной сеткой. Ограничились сеткой с квадратной ячейкой размером 2 мм.

Прокатку образцов осуществляли с обжатиями 2; 5; 10; 16 % с двойной кратностью повторения опытов. При этом также фиксировали усилие прокатки.

С целью повышения точности результатов координатная сетка, полученная на недокатах, сканировалась и затем обрабатывалась на компьютере с использованием приложения КОМПАС-3D. В итоге были определены для разных обжатий фактические границы очага деформации, представленные на рис. 1.

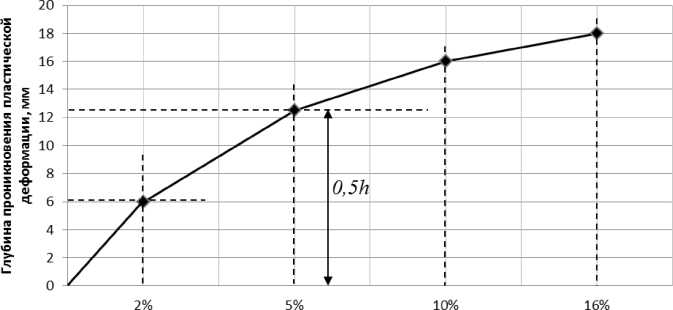
По результатам эксперимента также можно определить зависимость глубины проникновения пластической деформации от степени обжатия.

График зависимости степени проникновения пластической деформации от величины относительного обжатия для условий эксперимента, представлен на рис. 2.

Как видно на рис. 1 и 2 пластическая деформация не проникает на всю глубину при обжатии до 5 %, но следует отметить, что при обжатии от 5 % до 16 % пластическая деформация проникает на всю глубину лишь частично.

Решение задачи методом линий скольжения начинается с построения сетки линий скольжения [2]. В общем случае, сетку линий скольжения с учетом экспериментальной информации можно представить так, как показано на рис. 3.

Выполненные экспериментальные исследования позволили конкретизировать форму сетки линий скольжения для случая процесса прокатки с обжатиями до 5 %.

При построении сетки линий скольжения учитывались граничные условия на линии АЕ [2]:

1 f

Ф = ф±— arccos — + m п ;

2 т ,                              (1)

п L +т5sin^-vX где ф - угол между касательной к линии скольжения и осью Ох; ф - угол между нормалью к рассматриваемой границе и осью Ох; f. - касательное напряжение на рассматриваемой границе; fn – нормальное напряжение на рассматриваемой границе; т5 - сопротивление деформируемого металла пластической деформации сдвига.

На первом шаге построения рассчитывается положение точки С 2 , характеризующей положение нейтрального сечения. Для первого приближения воспользуемся зависимостью Экелунда–Пав-лова [3]:

Y=a o ( 1 -^ 0 ) ,                       (2)

2 V Ц J где ц - коэффициент трения; а0 - угол захвата, рад.

» 0 -^,                       (3)

где A h - абсолютное обжатие, мм; R - радиус валков, мм.

Угол между нормалью к рассматриваемой границе и осью Oх может быть определен как:

а)

! ya 02 uKofoi

-0.02

IV

V

-0.01

0.00

-0.01

0.00

-0,04

0.00

0.00

V/ 0.00S-003

V!

V

IV

m

II

/

0.00

0.00

-0.01 1 -0.03

-0.03 1 -0.01

0.00

0,00

-0,01

-0.03

-0.01

-0,01

-0.01

0,00^

-0.04

-0,03

-0,01

0,00.

-0,02

-0.01

-0.01

-0.02

-0,01

-0.01

-0,01

-0,01

-O.O1	-0,02\	0.00	-O.O1#
-0,01 ■-----	-0,01	0.00	оло
-0,01	-0,01	-0,02	f0,00

0,00

-0.01

0.00

-0,01 -0,01

-0,01

-0,01*

0.00

'0,00

0.00X0.00

-0.01

-0.01

-0.02

-0.02

0.00

0.00

-0.01

-0.05

-0.03

-0,01

0,00

0,00

0,00

0.00

0.00

0.00

0.00

0.00

'0.00

0.00

-0.01

-0.02

-0.01

-0.01

*0.00

0.00

0.00

-0.01

-0.02

-0.02

0.00

x0.00

-0.01^

-0.01\ -Q06

-0,01

-0,02

-0.01

-0.06

0,00

0,00

•0,00

-0,02

0,00

0,00

0,00

0,00

0.00

0,00

0,00

0,00

0,00

0.00

0,00

0,00

0,00

OX

0.00

0.00

-0,01

0.00

0.00

-0,01

0,00

0,00

-0,08

-0.01*

-0,01

-0,01

-0,01

-0.02

-0.03

0.00 0.00

-0,02 -0.01

-0.01 1 -аот

-0,01

0,00 -0,03 -0.02

-0.02\-0.01

-0.01 \ -0.01

- 0,04^-0,04 -0,02-0 03

-Q07 - Ю^ -0.01 _

\Лр1 0,00 QOO^O.OO "-001^^3-0,02 -0,02 "OOI ■

-qoi ООО -003 -001 -oof

-0.01 "^001

-0.05

-004

-00^ -801

-ooiV_qoi

-0.01

-001

-003 -0,01

-005

-001 \-001\ -0,02\ -0.01

-001

-001

-0.01 „001.

-QOO

-0,02 000.

0.00 \o,oo

-002

-003

-(№2\

*-0.01

-001

в)

б)

г)

Рис. 1. Форма очага деформации при прокатке полосы при обжатии 2 % (а), 5 % (б), 10 % (в), 16 % (г)

Степень деформации, %

Рис. 2. Зависимость глубины проникновения пластической деформации от обжатия

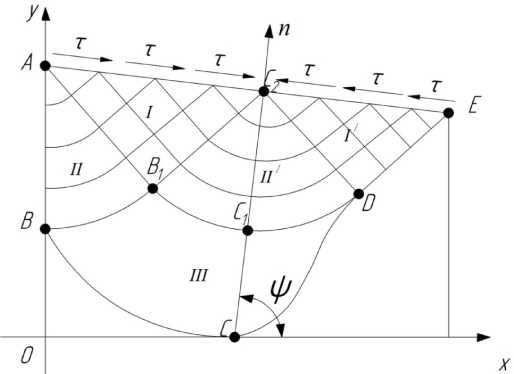
Рис. 3. Сетка линий скольжения

п п у =--а = —

2     к 2

—

, Га h arctg I — ,

V ^{2 1} о.д у

где lо д - длина очага деформации, мм; а к - угол конусности, рад.

На втором шаге ведется расчет основных углов сетки линий скольжения (рис. 4):

^Z B i AC 2 = ф от ^—а к = У ^— “arccosц ^—а к ,   (5)

где ф _от - угол между касательной к линии скольжения и осью Ох , рассматриваемый для зоны отставания.

Z С 2 ED = ф_оп — а k = у + ^-arccos ц + а k , (6) где ф _оп - угол между касательной к линии скольжения и осью Ох , рассматриваемый для зоны опережения.

Угол раскрытия центрированного веера:

0 = п — (а1 + а2) = п + у — -^-arccos ц — у —

——arccos ц = п — arccos ц.

Согласно сетке линий скольжения, представленной на рис. 3, для области I-I решается смешанная задача, для области II-II ' – вырожденная задача Римана, для области III – задача Римана.

После построения сетки линий скольжения строится математическая модель на основе решения стандартных задач, указанных выше. Для этого определяется напряженное состояние в каждой точке.

Осуществим переход от точки B к точке B ₁ вдоль семейства линии скольжения семейства а BB 1 . Согласно уравнению Генки, можно записать [2]:

СТ B — 2т s Ф B = СТ B1 — 2т s Ф B1. (8)

В точке B ₁ и соответственно во всей области AB ₁ C ₂ среднее нормальное напряжение будет равно:

с = —т _s ( 1 + у — arccos ц ) . (9)

С другой стороны, согласно граничным условиям AC ₂ среднее нормальное напряжение в треугольнике AB ₁ C ₂ будет равно:

с = fn +т s Sⁱⁿ⁽ Ф ^—у ). ⁽¹⁰⁾

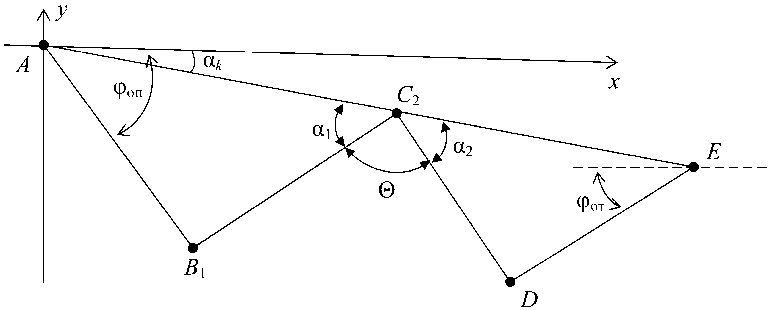
Рис. 4. К определению углов сетки линий скольжения

Решая совместно уравнения (9) и (10), получим нормальное напряжение на границе AC2, равное fn = -Ts [sm(v-W) + (1 + Y-arccosh)].   (11)

Аналогичным образом осуществляются переходы для других областей (точек).

Касательную составляющую усилия (напряжение трения) предпочтительнее задавать с помощью формулы Зибеля:

f _t=Mt s ,                                (12)

где h - коэффициент трения.

На основе всех выкладок модель определения

усилия примет вид:

P =

- 0,58 c s

• ( 1

sin - arccos h

V 2

^-a k

(

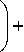
+V ¹

П

+ - - arctg

[iT ¹ ]

V 2 l о.д )

)D ^arccos h

J]J

+

0,5

+ ( 0,58 c _s h ) ² ] .                            (13)

В таблице приведено сравнение результатов расчета по формуле (13) с экспериментальными

данными.

Поставленный эксперимент позволил изучить форму, а также изменение формы очага деформации при различных назначенных режимах. Метод линий скольжения позволил теоретически получить модель усилия, которая подтвердилась проведённым экспериментом; сравнение расчетных и экспериментальных значений представлено в таблице и на рис. 5. На рис. 6 показаны экспериментальные значения энергосиловых параметров прокатки I образца при обжатии 2 %.

Выводы

• 1.    Экспериментальные исследования показали, что при степенях обжатия высокой полосы, не превышающих 5 %, пластическая деформация не проникает на всю глубину листа по толщине.

• 2.    Для определения усилий, возникших при прокатке высоких полос с малыми обжатиями, предложено использовать метод линий скольжения. Погрешность расчетов по математической модели, построенной на основе этого метода, не превышает 7 %.

• 3.    Полученные данные могут быть использованы при проектировании технологии и оборудования для обжатия кромок листа в линии станов горячей прокатки.

Расчетное и экспериментальное значение усилия

Параметр	Степень деформации
	2 %	5 %	10 %	16 %
P расч , кН	1,133	1,62	2,112	2,511
эксп , к	1,12	1,50	1,79	2,24
Δ, %	1,17	7,4	15,2	10,8

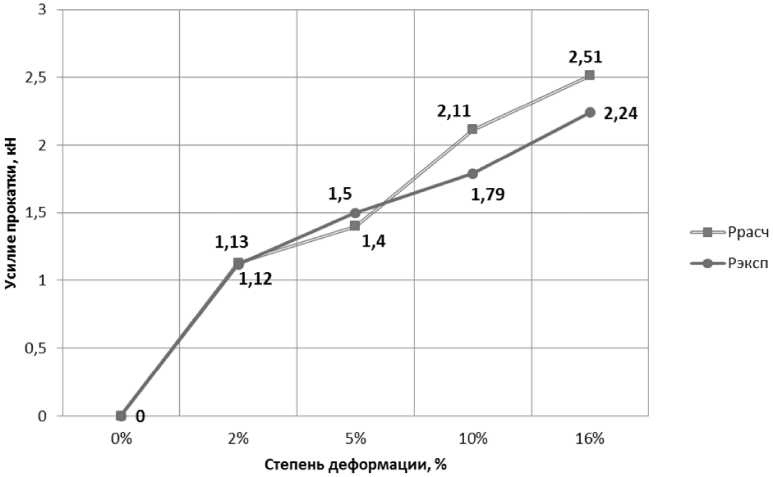
Рис. 5. Расчетное и экспериментальное значение усилия

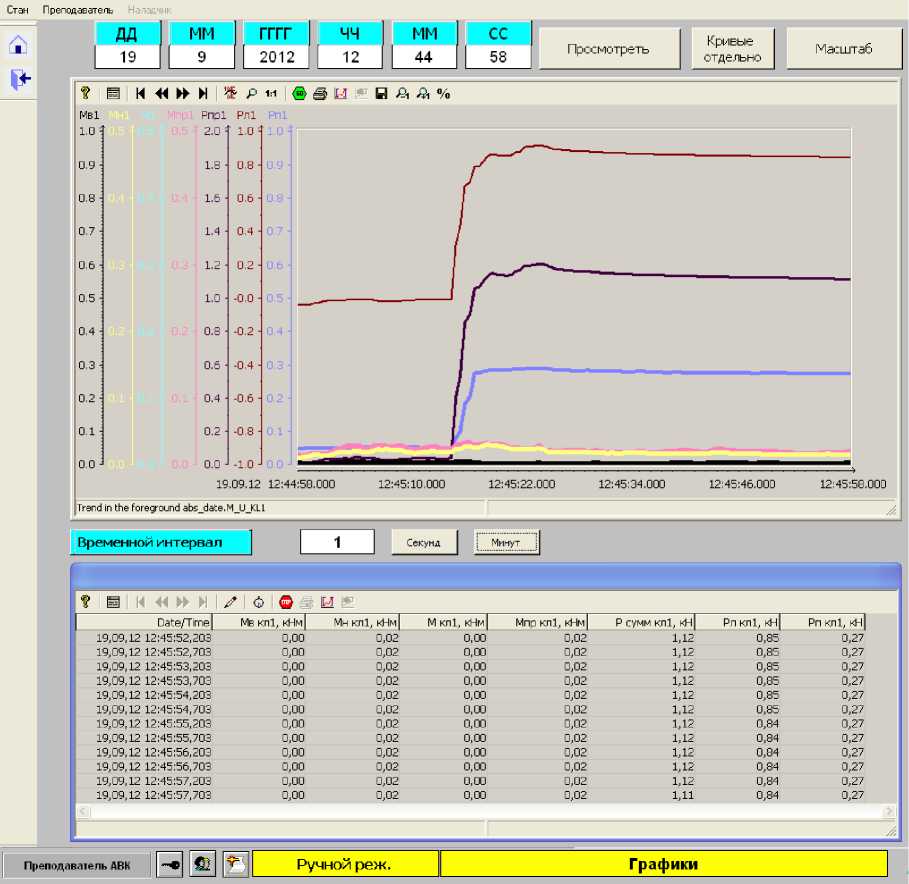
Рис. 6. Экспериментальное показание усилия прокатки при обжатии 2 %