Исследование процесса съёма металла при абразивной галтовке

Введение. Развитие машиностроения на современном этапе невозможно без постоянного повышения производительности труда и улучшения качества выпускаемых изделий. В машиностроении всё более широкое применение находят методы обработки абразивным инструментом. Абразивная обработка позволяет обеспечить требуемые точность и качество деталей при высокой производительности, а также высокую надёжность и долговечность машин в процессе эксплуатации, поэтому роль абразивных операций в современном машиностроении непрерывно возрастает.

Стремление удешевить окончательную обработку привело к созданию новых методов обработки — свободными абразивами, в которых инструмент не имеет жёсткой кинематической связи со станком.

При обработке свободными абразивами зёрна более полно используют свои режущие способности, так как происходит равномерное распределение их режущих кромок относительно обрабатываемых поверхностей, а также переориентация и перемещение в процессе обработки.

Методы обработки свободными абразивами позволяют осуществлять обработку деталей сложной конфигурации, в больших размерных диапазонах, из различных материалов, используя при этом сравнительно простое и надёжное в эксплуатации оборудование. Значительно снижается, по сравнению со шлифованием, и температурный режим процесса, так как скорость резания снижается, а зоны микрорезания обильно омываются технологической жидкостью (ТЖ). Все эти факторы позволяют получать высокое качество обработанной поверхности без прижогов, микротрещин и нежелательных структурных изменений.

Сущность метода галтовки заключается в очистке и отделке (шлифовании, полировании) поверхности детали путём совместного пересыпания с абразивом в барабане. При вращении барабана (или колокола) обрабатываемые изделия вместе с абразивными частицами (гранулами) беспорядочно перемещаются и трутся друг об друга, в результате чего с поверхности снимается слой металла. Барабаны могут быть цилиндрическими, многогранными, бочкообразными с двумя или тремя внутренними рёбрами и объёмом до 4 м3. При частоте вращения барабана 10– 50 об/мин, объём абразивного материала в 3–8 раз должен превышать общий объём деталей, а объём всей массы загрузки (деталей и абразива) не должен превышать более 60 % объёма барабана. Существует сухая и мокрая (жидкостно-абразивная) галтовка.

До настоящего времени исследования по выявлению влияния технологических параметров на выходные показатели обработки галтовкой практически не проводились, что ограничивало применение этого высокопроизводительного метода. В литературе отсутствует теоретический анализ влияния режимов обработки и характеристик обрабатываемой среды на производительность и качество обработки. Существуют лишь отдельные рекомендации по выбору определённых технологических параметров, носящие в основном рекламный характер.

В связи с вышеперечисленными факторами, дальнейшее развитие технологии галтовки и её промышленное освоение невозможны без создания теоретической модели процесса, отражающей его физическую сущность и позволяющей прогнозировать результаты обработки на стадии проектирования.

Исследование единичного взаимодействия. При исследовании основных технологических параметров галтовки (производительности процесса и качества обработанной поверхности) необходимо решить задачу теоретического моделирования процесса единичного взаимодействия абразивных частиц с поверхностью обрабатываемой детали. Разработка теоретических зависимостей, описывающих форму и размеры следов обработки, позволит в дальнейшем перейти к теоретико-вероятностному описанию распределения следов на поверхности детали, что, в свою очередь, даёт возможность разработать модель формирования профиля шероховатости и удаления металла с поверхности детали.

Процесс единичного резания при абразивной обработке рассматривается во многих работах [1, 3, 4], так как он является основополагающим, раскрывает сущность абразивного воздействия и даёт возможность определить оптимальные технологические режимы обработки деталей машин.

Анализ работ [1–3] позволяет предположить, что взаимодействие абразивной частицы с поверхностью детали происходит следующим образом. При ударе частицы, движущейся под некоторым углом β к поверхности детали, на неё действует сила сопротивления P , которую можно разложить на нормальную P_N и касательную P _τ . Известно [1], что при нормальном заглублении, единичный индентор будет охватываться деформируемым материалом равномерно со всех сторон. При приложении тангенциальной нагрузки напряжения со стороны действия тангенциальной силы возрастают и абразивная частица начинает двигаться, пластически оттесняя материал. При этом задняя полуповерхность, по направлению движения этой частицы, окажется полностью разгруженной, то есть она оторвётся от ранее деформируемого материала. Так как средние нормальные напряжения на поверхности контакта в статичном состоянии приблизительно равны средним нормальным напряжениям при движении, то очевидно, что в момент начала скольжения площадь на передней полуповерхности индентора должна возрасти, тем самым компенсируя отсутствие её на задней полуповерхности. Это приведёт к заглублению индентора до тех пор, пока площадь передней полуповерхности не достигнет определённого значения. Соответственно будет возрастать тангенциальная сила, которая при равенстве поверхностей достигает своего максимального значения (если пренебречь реологическим эффектом). В результате этого происходит дополнительное углубление индентора h .

При таком перемещении частицы на неё действует реакция со стороны материала детали, одна составляющая которой касательная — сила трения, тормозящая движение, а другая нормальная, стремящаяся вытолкнуть частицу из материала. При соударении твёрдых тел обе составляющие обычно уравновешиваются внешними усилиями, то есть динамическими силами, определяемыми ускорением и массой частицы. По мере увеличения силы взаимодействия P кон- тактные напряжения, или деформации, возрастают и могут достигнуть разрушающих величин. В этом случае происходит переход к микрорезанию.

Согласно [2, 4] процесс снятия стружки становится возможным при напряжениях по линии скалывания, обычно превышающих сопротивление материала срезу. Установлено, что при углублении сферического индентора металл по краям выпучивается, и углубление происходит до тех пор, пока напряжение на контактной поверхности не станет равным c σ _s , где σ _s — предел текучести материала детали, оценивающий несущую способность контактной поверхности. По данным [2, 4] значение этого коэффициента колеблется от 1 до 6, для металла в нормальном состоянии, и достигает 10 при наличии наклёпа. При определённом углублении, когда напряжение на контактной поверхности достигает вышеуказанных значений, наступает затормаживание металла перед частицей, обтекание прекращается и начинается нагребание металла, то есть идёт процесс микрорезания. Сдвиг металла происходит в направлении движения в плоскости касания.

На основании анализа работ [1, 3] предлагается следующая методика определения съёма металла с поверхности детали при единичном взаимодействии. Пусть абразивная частица, имеющая характерный размер R (радиус описанной окружности), движущаяся со скоростью Vч под углом β к поверхности детали, ударяется о неё с силой, достаточной для снятия стружки (здесь рассматриваются только те случаи взаимодействия, которые приводят к микрорезанию), тогда

V dV = д^- ■ dx , ^,

где L — средний диаметр пятна касания при ударе; dV — объём металла, удалённого на пути скольжения dx ; V_д — деформированный объём при взаимодействии сферической частицы с деформируемым пространством.

Воспользуемся соотношением, известным из теории скольжения жёсткой сферы по пла- стически деформируемому полупространству [2]:

L = 2 ^R^ ,

V =nRh2, где π — число пи. Тогда

π Rh ² dV = — . dx , 2dRh

.

Проинтегрировав (4) по пути скольжения частицы, получим x •

Для нахождения предела интегрирования введём безразмерные координаты: hx

£ = v— и ^ = v—, hmax        hmax где hmax — максимальная глубина внедрения частицы.

После преобразований получим:

Е , ( ^ , )

f £ 2 dx .

Для дальнейшего анализа воспользуемся тем, что удар жёсткой сферической частицы о деформируемое полупространство, ограниченное плоскостью, описывается системой уравнений:

d2h kmmdt^ = "PN ;

d2x kmmdtr = "Pt;

где m — масса частицы; k_m — коэффициент, учитывающий влияние соседних частиц при обработке; t — время.

Решение первого уравнения системы (8) можно найти, используя известное соотношение теории пластического контакта гладкого сферического индентора с деформируемым полупространством [2]:

P N = ^П ^hc ^О s . (9)

Так как при галтовке фактическая площадь контакта образуется в процессе дискретного взаимодействия группы абразивных зёрен, расположенных на сферическом сегменте, с поверхностью детали, в выражении (9) заменим R_сф на эквивалентный ему радиус частицы:

R э — k R R сф ,

где k_R — коэффициент, учитывающий влияние зернистости абразивной частицы на фактическую

площадь контакта.

Определение величины k_R будет представлено ниже.

Тогда

P N = nk R Rhc о _s .

После подстановки (10) в (8) получим:

d2h km —- = -nkRhco,, или m dt2 R s

d ² h   3 k_Rc σ _sh

---— —---— , dt ²    4 k m ρ ч R ^{2 ,}

где ρ _ч — плотность материала частицы.

Учитывая, что при t — 0, h — 0 и — = 0, получим:

dh — ± V ² sine - ³ ■ -k R c ⁰^ h ², dt ^ч 4 k m ρ ч R ^{2 ,}

а так как при h — h , dh — 0, то зависимость для определения максимальной глубины внедре-max dt ния частицы будет выглядеть следующим образом:

h max — 2k m⁵ V z R Sine, ^r^—

3 k_Rc σ _s

.

Для процесса галтовки примем допущение, что частица падает на деталь с высоты h_ч , равной 2/3 диаметра барабана:

V , — 2ghK — — 1,15 4gD 6 ,

где D_б — диаметр барабана, g — ускорение свободного падения.

Тогда максимальная глубина внедрения частицы определится по зависимости:

h max — 1,33km⁵R Sine

Перейдя к безразмерным координатам можно записать:

ρ _чgD_б k_Rc σ _s ^.

dh = ±V sinpVl - e2 ; dt ч dt = ±-----hmax dE

.

k 'V sinex'1   ^ 2

Учитывая, что PT = f ■ PN, где f — коэффициент пропорциональности, после преобразований по- лучим:

, f, ctge - f L dE = f ± ,       d e .                                     (12)

I      V1 - E² )

Здесь знак плюс соответствует увеличению внедрения ( d E >  0), а знак минус — уменьшению

(dE ^ 0). Используя (12), можно проинтегрировать (7). Предел интегрирования е, находим из условия, что скольжение прекращается либо когда — = 0, либо когда е = 0 . В первом случае из dt

(12) имеем е,

1 - ----- N I f tge

а во втором случае — е , = 0 .

Вид интеграла

A = ^E j e d E, 0

входящего в выражение (7), зависит от численного значения е,, то есть от величины произведе ния f ■ tgP . Учитывая, что по данным [2, 3], коэффициент трения абразивного зерна по металлу равен в среднем 0,25, а угол встречи с поверхностью детали для обработки свободным абразивом не превышает 45°, можно сделать вывод, что f ■ tge < 2.

Тогда интеграл (13) преобразуется к виду

A = 2(ctge - 1)J' d ^E .                                  (14)

0 V1 - E²

Интеграл, представленный в выражении (14), не берётся в конечном виде, но его можно выразить через гамма-функцию:

Г ( ⁵ )

A = Vn ( c tge - f ) .                                  (15)

Г I ⁷ I

I 4 7

Подставляя значения гамма-функции, получим

A = 1,75 ■ ( c tge - f ) .

Подставляя (16) в выражение (7), после преобразований получим зависимость для определения объёма металла, удалённого за один удар абразивной частицы:

з

V = 1,46 Ry k R ⁴

f sine km5

I

ρ _чgD_б с σ _s

| 2

( ctge - f ) .

Соответственно, съём металла за один удар абразивной частицы

R^з q = ^1,46 k ⁴

Sine km'

I

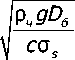
A 2

( ctg^e - f ) p д ,

где ρ _д — плотность материала детали.

Для удобства записи и пользования зависимостью (18) введём новый коэффициент k, =                                      d9)

k R ⁴

и назовём его коэффициентом, учитывающим влияние зернистости абразивной частицы на съём металла. Тогда зависимость для определения съёма металла при единичном взаимодействии за- пишется в виде:

q = 1,46k₃R³

( sine k m

I

ρ _чgD_б с σ _s

A 2

( ctg^e - f ) p д .

Для учёта влияния зернистости абразивной гранулы на съём металла воспользуемся методикой работы [4]:

r

^k R = 3

63,5 gD 6 p , c σ _s

^{( k} p ^km⁵ sinpx ^ ( ^a )( 1 - E з ) x ^A 2

^         a² ( x ²+ 3a² )         ₇

где a — коэффициент формы зерна; Y(a) — функция, зависящая от a; х — доля, занимаемая зёрнами в грануле; εз— коэффициент, учитывающий заделку зёрен в связке; x — средний размер зерна; σ — среднее квадратичное отклонения размеров зёрен.

Исследование процесса удаления металла. Общее количество взаимодействий на площади квадрата упаковки (в случае упаковки абразивных частиц на поверхности детали по квадрату, со стороной, равной диаметру описанной окружности), приводящих к микрорезанию, можно определить следующим образом:

np = PiP2fet, где P1 — геометрическая вероятность события, заключающегося в том, что любая точка квадрата упаковки покрывается пятном контакта за один цикл воздействия массы абразивных частиц; P2 — вероятность события, заключающегося в том, что взаимодействие абразивной частицы с поверхностью детали приведёт к микрорезанию; fв — частота циклов воздействия массы аб- разивных частиц на поверхность детали; t — время обработки.

Как показано в [3], большинство взаимодействий абразивных частиц с поверхностью детали происходит под острым углом, следовательно, пятно контакта при единичном взаимодей- ствии можно представить в виде эллипса.

Задача заключается в определении вероятности того, что любая точка внутри квадрата упаковки может быть покрыта одним эллипсом. Однако ввиду того, что в реальном процессе обработки взаимодействие абразивной частицы с поверхностью детали имеет более сложный характер, дадим оценку вероятности. Применительно к процессу вибрационной обработки такая модель рассмотрена А. П. Бабичевым в работе [6], при этом оценка искомой вероятности снизу равна

P =      ⁿab

1 па2 + 4Da + D2, где a и b — большая и малая полуоси эллипсов контакта; D — диаметр абразивной частицы.

В обычном случае, когда площадь поверхности детали больше квадрата упаковки, общее число взаимодействий, приводящих к микрорезанию равно

S дет

NP  np c , кв.уп.

где S_дет — площадь поверхности детали; S_{кв . уп .} — площадь квадрата упаковки.

Приняв S_KByn = D ² = 4 R ², получим

N = PPftS⁵ ^ . р 1 2 в 4 R 2

Следует учитывать, что в случае обработки очень малых деталей, либо их отдельных участков, когда площадь детали меньше площади квадрата упаковки, значение вероятности P1 изменится и составит

P = nab

.

дет

При этом зависимость для определения общего числа взаимодействий, приводящих к микрорезанию, примет вид:

N = p P 2 f_Bt .                                      (26)

Для проведения расчётов необходимо определить величину полуосей эллиптического пятна контакта a и b , воспользовавшись геометрической схемой внедрения абразивной частицы в поверхность детали.

Как показано в работе [4], величину полуосей эллипса контакта при обработке свободными абразивами, в том числе и при галтовке, можно найти по зависимостям:

Ь = ^R2 - (R - h max)2 , a =

2 ■ ( ctga - f ) ■ h max + b .

Ранее отмечалось, что разрушение поверхностного слоя при галтовке происходит преимущественно путём микрорезания. Следовательно, при расчёте съёма металла достаточно учитывать только число взаимодействий N_p , приводящих к микрорезанию:

Q = Npq, где Q — съём металла с поверхности детали.

Подставив значение N_p из рассмотренных выше зависимостей, получим:

Q = P i P 2 f e tq R при S gem > 4 R ²,                            (28)

Q = P 1 P 2 f e tq при S gem < 4 R ².                                 (29)

Для проверки полученной зависимости, произведена серия экспериментальных исследований процесса абразивной галтовки. Определялось влияние зернистости абразивных гранул и механических свойств обрабатываемых материалов на съём металла с образцов площадью S_geT = 10 см².

Результаты сравнения теоретических и экспериментальных исследований в таблицах 1 и 2.

Таблица 1

Влияние зернистости абразива на съём металла при галтовке

Зернистость	Q теоретический (кг)	Q экспериментальный (кг)
4	7,48*10-9	7,6*10-9
8	1*10-8	1,2*10-8
16	1,36*10-8	1,5*10-8
25	1,64*10-8	1,8*10-8
40	2,0*10-8	2,4*10-8

Таблица 2

Влияние предела текучести материала детали на съём металла при галтовке

σ s (МПа)	Q теоретический (кг)	Q экспериментальный (кг)
200	8,83*10-8	9*10-8
300	5,1*10-8	5,5*10-8
400	3,5*10-8	4,2*10-8
600	2,0*10-8	2,3*10-8

Заключение. Анализируя результаты теоретических и экспериментальных исследований, можно сделать вывод о том, что полученные зависимости могут быть использованы при технологических расчётах параметров абразивной галтовки.