Исследование процесса сушки текстильных и обувных влажных материалов методом регулярного режима

Основные теплотехнические операции текстильной и обувной промышленности показывают, что и на промежуточных, и на заключительных стадиях обработки материалов необходима сушка. В процессе технологической обработки материалы подвергаются различным технологическим операциям – аппретированию, мерсеризации, крашению, жированию, дублению и прочим. Такое значительное число операций предъявляет к сушке и сушильному оборудованию ряд требований.

Правильно организованный процесс сушки должен улучшать технологические свойства, сокращать длительность сушки и уменьшать энергозатраты на процесс. В текстильной и обувной промышленности широко используется конвективная сушка нагретым воздухом, как менее энергозатратная по сравнению с другими методами энергоподвода.

В процессе сушки влажных материалов происходит непрерывное изменение температуры и влагосодержания. При этом в материале возникают градиенты влагосодержания, которые могут вызывать изменение структурно-механических свойств, коробление и разрушение материала.

Поэтому необходимы простые, надежные методы расчета основных параметров кинетики сушки, позволяющие отслеживать изменение температуры и влагосодержания в процессе.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим сушку тонких материалов в виде неограниченных пластин толщиной RV = δ, где RV – отношение объема тела к поверхности. Начальное распределение температуры и вла-госодержания равномерное. В начальный момент времени материал помещается в среду с постоянной температурой tc = const и проходит сушку. Между ограничивающими поверхностями материала со средой при tc = const происходит конвективный теплообмен по закону Ньютона. Необходимо найти закономерности распределения температуры, влагосодержаний в материале и определить плотности тепловых потоков в процессе сушки. Такие задачи относятся к решению дифференциальных уравнений тепломассо-переноса при граничных условиях третьего рода и к задачам теории регулярного режима применительно к процессам сушки.

РЕГУЛЯРНЫЙ ТЕПЛОВОЙ РЕЖИМ

Рассмотрим основные положения теории регулярного режима. Основным признаком ре- гулярного режима для процесса конвективной

где dt / dτ и d u / dτ — скорости регулярного нагревания тела и убыли влагосодержания; m_t и m_u — темп нагревания тела и темп убыли вла-госодержания в материале; t_c — температура теплоносителя; t — среднеинтегральная температура материала; u₀ и u — начальное и текущее влагосодержание материала.

Величины m_t и m_u играют центральную роль в теории регулярного режима и определяются экспериментально при построении зависимостей

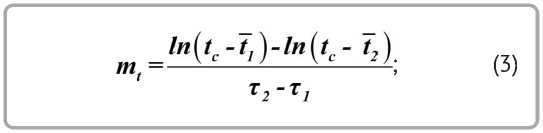
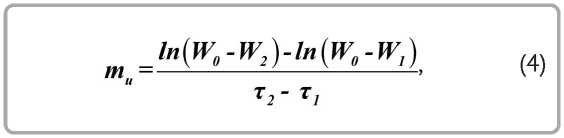
при т = 0 , В = t 0 , где t₀ — температура материала в периоде постоянной скорости сушки.

Решение уравнения (7) можно записать в виде [1]

где t 1 , t₂ , W 1 , W₂ , т 1 , t ₂ - фиксированные значения температуры, влагосодержания и интервалы времени сушки; W₀ – начальное значение вла-госодержания.

Величина темпа нагревания влажного тела любой формы на основании (1) определяется из балансового уравнения энергии [1, 2]:

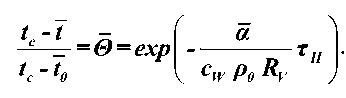
V dt            x                 \

, (5)

F dr

где ñ_W — теплоемкость влажного материала, Дж / кг °С; p 0 — плотность, кг / м 3 ; V — объем тела, м³; F — поверхность, м²; t_n — температура поверхности материала, °С; а — коэффициент теплообмена между поверхностью и средой, Вт / м² °С.

Из решения уравнения (5) следует:

где 0 - относительная избыточная температура материала; т_п - время сушки во втором периоде.

Следовательно, процесс нагревания влажного тела описывается простой экспонентой. При сушке тонких плоских влажных материалов критерий Bi < 0,1 (практически достаточно Bi < 0,4), а критерий у ^ 1, и можно пользоваться формулой (8) [2, 4]. Из уравнения (6) при условии Bi < 0,4 и у = 1 следует:

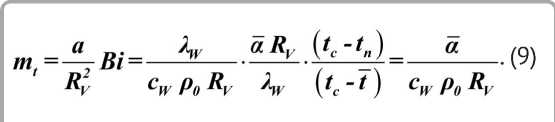
к                                                                             /

Тогда на основании (8) для относительной

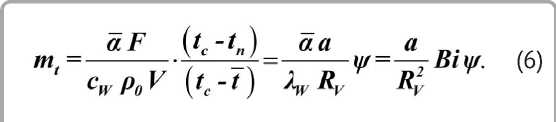
k                                                                        /

температуры получим

Здесь Bi = а R V / A W - критерий Био; a = A W / c_Wр₀ - коэффициент температуропроводности, м 2 / ч; A W - коэффициенттеплопровод-ности влажного материала, Вт / м °С.

Коэффициент неравномерности распределения температуры во влажном материале

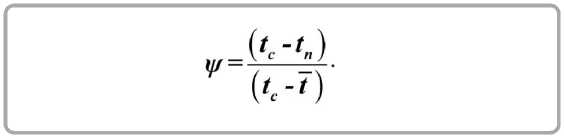
Интегрируя левую часть уравнения (5), получим [3]:

.                (7)

cw Ро Ry

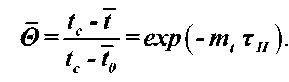
В соответствии с теорией подобия величина m_t т_п представляет обобщенную комплексную переменную процесса сушки [5].

Секундный поток теплоты находится из уравнения баланса

-     о dt . dr	(11)

Дифференцируя решение (8) и подставляя результат в (11), получим [3]:

^Чп _ ~схр

а

-------^тп ^cw Ро ^г

, (12)

Постоянная B определяется из начального условия: для периода убывающей скорости сушки где теплота qI = а (tc - t0) = акр (tc -t0) есть теплота, подводимая к материалу в первом периоде сушки; qÏ – теплота, затрачиваемая на испарение влаги из материала во втором периоде сушки; акр - коэффициент теплообмена в первом периоде сушки, Вт / м2 °С.

Уравнение (12) запишем в следующем виде:

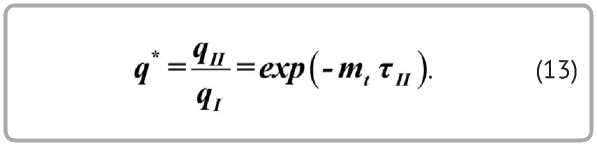
Сравнение уравнений (10) и (13) устанавливает, что регуляризация процесса теплообмена происходит и по температурам, и по тепловым потокам.

Из решения дифференциального уравнения тепломассообмена для влажной неограниченной пластины при граничных условиях третьего рода (сушка) А.В. Лыковым [2] получены зависимости для безразмерных потенциалов переноса тепла и вещества:

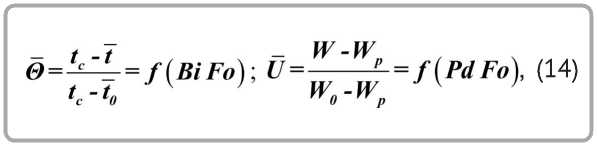
где U – относительное влагосодержание материала; критерий Фурье Fo = ат / R 2V , критерий Предводителева Pd = kR²_V / a , k – коэффициент сушки, c^-1, мин^-1; W_P – равновесное влагосодер-жание материала, %.

Исходя из терминологии теории регулярного режима запишем критерий Предводителева в виде pd=muRV а

,

где m_è – темп удаления влаги из материала, c^-1, мин^-1.

Комбинации критериев Bi Fî и Pd Fî представляют важные обобщенные переменные процесса сушки:

. (15)

• ¹¹             a Ry

Следовательно, темп нагревания материала m_t и темп убыли влагосодержания m_è зависят от критериев Bi , Fî и Pd .

Введение в практику сушки таких обобщенных параметров придает исследованию сушки обобщенный характер, сближает практику с теорией и сокращает число необходимых экспериментов [5].

Инвариантность величин m_tT_n и т_ит при заданном влагосодержании материала независимо от режима сушки представляет собой наиболее общие закономерности кинетики сушки влажных материалов при различных методах энергоподвода [5].

Таким образом, на основании (15) запишем:

;                 (16)

.                  (17)

ОБРАБОТКА ЭКСПЕРИМЕНТА И ВЫВОД РАСЧЕТНЫХ УРАВНЕНИЙ

На рисунках 1 а , б и 2 а , б изображены типичные температурные кривые t = f ( u ), t = f ( т ) и кривые сушки W = f ( т ) для процесса сушки подошвенной кожи и шерстяного войлока при различных режимах. Видно, что при сушке тонких материалов ( R V = 8 = 4-8 мм) и критерии Bi < 0,4 наблюдаются период постоянной скорости сушки и период постоянной температуры. Переход от первого периода сушки ко второму происходит при достижении первого критического влагосодержания W_кр .

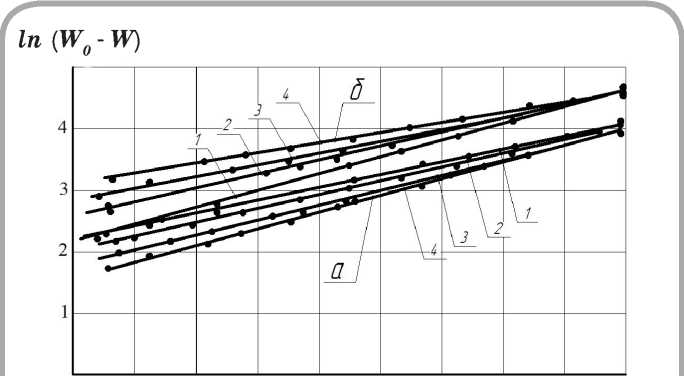
Обработка экспериментальных данных по сушке подошвенной кожи и шерстяного войлока по уравнениям (3) и (4) представлена на рисунках 3 а , б и 4 а , б . Изображенные графические зависимости имеют вид прямых. Следовательно, распределение температуры и влагосодержания внутри влажного материала описывается простыми экспонентами и не зависит от начального распределения температуры и влагосодержания [1, 2, 4].

Получены следующие значения для темпа нагревания влажного материала: для подошвенной кожи m_t = 0,04 мин^-1 (при режимах сушки t c = 40,50,60 °С; скорости воздуха и = 3,5 м / с); для шерстяного войлока m_t = 0,02 мин^-1 (при ре-

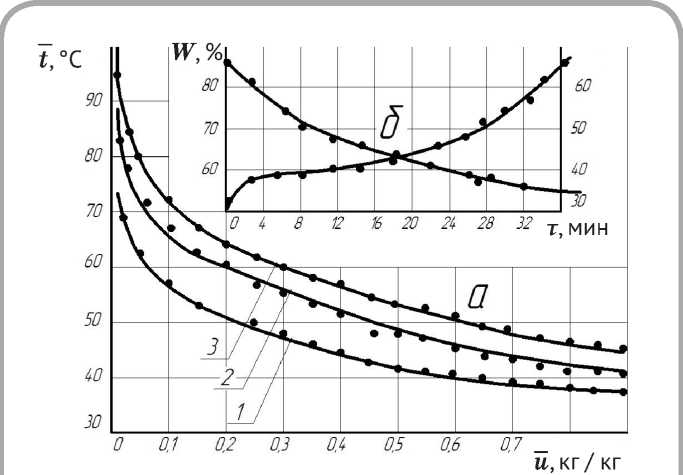
Рисунок 2 – Температурные кривые t = f ( u ) ( а ) и t = f ( τ ) и кривые сушки W = f ( τ ) ( б ) для процесса сушки шерстяного войлока при режимах:

1 – t_ñ = 90 °С ; υ = 3 м /с ; 2 – t_ñ = 120 °С ; υ = 5 м ^ñ / с ; 3 – t_ñ = 150 °С ; υ = 10 м / ^ñ с

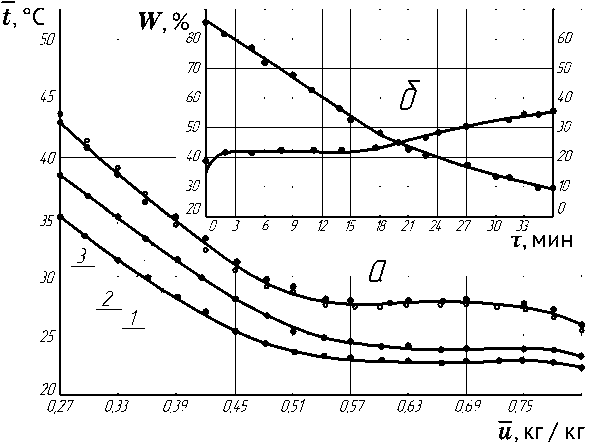
Рисунок 1 – Температурные кривые t = f ( u ) ( а ) и t = f ( τ ) и кривые сушки W = f ( τ ) ( б ) для процесса сушки подошвенной кожи при режимах: 1 – t_ñ = 40 °С ; υ = 3 м / с ; 2 – t_ñ = 50 °С ; υ = 5 м / с ; 3 – t_ñ = 60 °С ; υ = 5 м / с

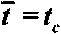
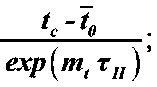
1 W-W_p т_и W₀-W_p

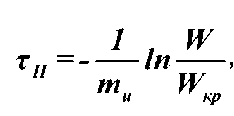
при w .

Температура влажного материала в первом периоде сушки приближенно вычисляется по выражению

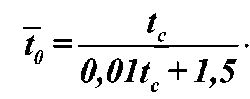
жимах сушки t_c = 90, 120, 150 °С; скорости воздуха υ = 3, 5, 10 м / с).

На рисунках 5 и 6 а , б представлена обработка опытных данных по уравнениям (16) и (17). Видно, что при сушке подошвенной кожи и шерстяного войлока при различных режимах все экспериментальные точки укладываются на кривые с разбросом в пределах точности проведения эксперимента.

Решением уравнений (16) и (17) определяются среднеинтегральная температура длительности процесса сушки:

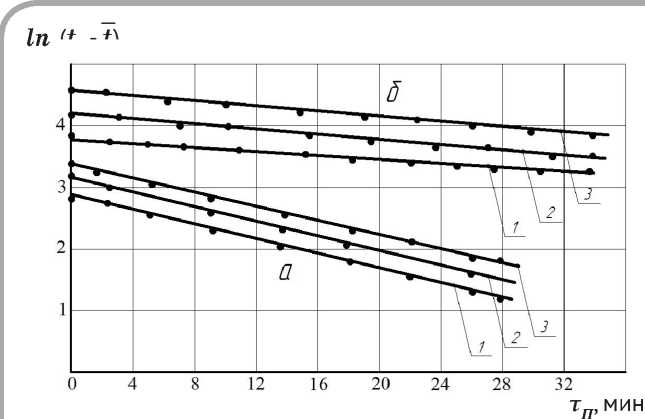
Рисунок 3 – Зависимости ln ( t_c - t ) = f ( τ_Ï ) для сушки подошвенной кожи ( а ) и шерстяного войлока ( б ) при режимах, указанных на рисунках 1 и 2

0     4      8     12     16     20    24     28     32

T, МИН

Рисунок 4 – Зависимости ln ( W₀ - W ) = f ( τ ) для сушки подошвенной кожи (а) и шерстяного войлока (б) при режимах, указанных на рисунках 1 и 2

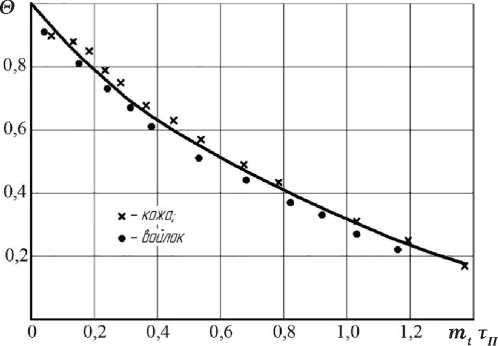
Рисунок 5 — Зависимость Θ = exp ( - m_t τ_Ï ) для сушки подошвенной кожи и шерстяного войлока при режимах, указанных на рисунках 1 и 2

где N – скорость сушки в первом периоде, мин^-1.

На рисунке 6 б дана зависимость m_u = f ( N ) для процесса сушки подошвенной кожи и шерстяного войлока при различных режимах.

Плотности тепловых потоков для периода убывающей скорости сушки вычисляются по уравнению (13)

_Чп=_Ч1ехр^-т, т^ .         (23)

Плотность потока тепла в первом периоде определяется по выражению qi=rPoRvN, Вт / м2

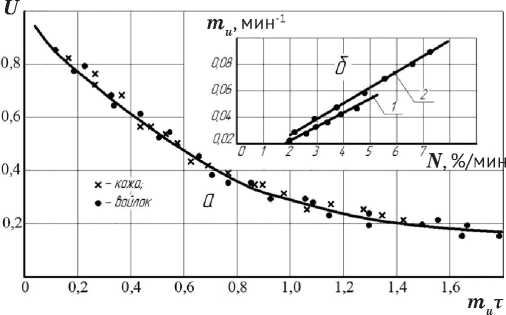
Рисунок 6 – Зависимости U = exp ( - m_t τ_Ï ) ( а ) и m_è = f ( N ) ( б ) для сушки подошвенной кожи и шерстяного войлока при режимах, указанных на рисунках 1 и 2

Темп убыли влагосодержания m_u оказывается сложной функцией режима сушки, начального влагосодержания W₀ , скорости сушки в первом периоде N , способа подвода теплоты к материалу и прочих факторов, воздействующих на процесс.

Экспериментально установлено, что величина m_u прямо пропорциональна скорости сушки в первом периоде N и не зависит от начального влагосодержания W₀ [4, 5].

В результате обработки эксперимента по сушке многих различных влажных материалов (более 15) для m_u установлено эмпирическое уравнение

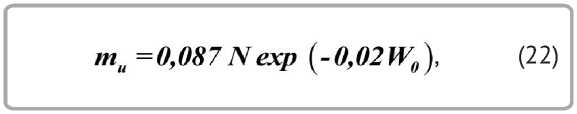
где r — теплота парообразования, Дж / кг;

N = dW / dτ = const , с^-1.

Обработкой опытных данных по сушке подошвенной кожи и шерстяного войлока получены простые зависимости для определения плотностей теплового потока для периода падающей скорости сушки

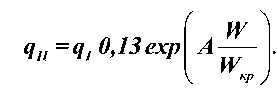
Коэффициент À принимает значения: для подошвенной кожи À = 2,5; для шерстяного войлока À = 3,7.

В таблице 1 представлено сравнение экспериментальных и расчетных значений температуры, длительности процесса сушки и тепловых потоков по уравнениям (18), (19), (20), (23) и (25).

В таблице 2 дан расчет кинетики сушки шерстяного войлока методом регулярного теплового режима. Сопоставление расчетных значений параметров кинетики сушки, вычисленных по формулам, с экспериментом находится в пределах точности проведения эксперимента, и погрешность в расчетах не превышает допустимых пределов.

ЗАКЛЮЧЕНИЕ

Метод регулярного режима нагревания твердых тел, применительно к процессам сушки влажных материалов, дает возможность, не при-

Таблица 1 – Сравнение экспериментальных и расчетных значений температуры и длительности сушки, полученных на основе уравнений (20) и (18) для процессов сушки подошвенной кожи и шерстяного войлока

Подошвенная кожа (рантовая) δ = 3,5 мм; W₀ = 86 %; W_кр = 57,5 %

Режим сушки: t_c = 60 ° C; скорость воздуха υ = 3 м / с; N = dW / d τ = 3,15 % / мин

W , %	τ П экс , мин	τ П рас , мин	tэкc , ° C	tрас , ° C	τ экс , мин	τ рас , мин	qÏ , Вт / м2	qÏ , Вт / м2
		(20)		(18)		(19)	(23)	(25)
45	5,7	5,2	32	31	15,0	16	3510	3650
39	8,2	7,8	36	37	18,0	19	3170	2880
33	11,5	10,8	38	40	24,5	23	2780	2500
24	19,0	17,7	45	46	32,7	38	2060	1840
21	27,0	26,0	48	48	40,0	45	1650	1410
		Шерстяной войлок δ = 8 мм; W0 = 114 %; W				= 74 %
		Режим сушки: tc = 90 ° C; скорость воздуха υ = 5 м / с				; N = 5,3 % / мин
50	5,6	5,5	41,0	42,0	13,5	13,2	4525	4200
40	9,1	8,6	44,5	45,5	17,1	16,7	4240	4360
30	12,5	12,2	48,0	48,7	21,5	21,2	2944	2720
10	26,0	25,3	57,0	57,5	37,0	38,0	2013	1600
к 5	30,0	29,0	62,0	65,0	40,0	38,0	1700	1200

Таблица 2 – Расчет кинетики сушки шерстяного войлока методом регулярного теплового режима

Последовательность расчета кинетики сушки шерстяного войлока. Режим сушки: tc = 120 °C; υ = 3 м / с; δ = 8 мм; W0 = 114 %; Wкр = 74 % Расчетная формула Расчет Эксперимент 1. Скорость сушки в первом периоде (W0 - Wкр )/ τ1 = N 6,00 6,13 2. Темп убыли влагосодержания mè = 0,11 N exp (- 0,02 W0) 0,048 0,052 3. Темп нагревания влажного материала mt = 0,115 exp (- 0,02 Wкр) 0,025 0,02 4. Время сушки в первом периоде τI = (W0 - Wкр )/ N 7,6 7,9 /   WK т =—In—— m„ W, 8,2 7,9 5. Длительность сушки до равновесной влажности Wp = 4 % при t = 20 °C, φ = 70 % 1 w„ T™=--1«-7 ma 51 49 6. Средняя по объему температура материала в первом периоде t0 = tc / (0,01 tc + 1,5) 44,5 45,0 7. Среднеобъемная температура материала в конце процесса сушки (Wp = 4 %) t= t tк =tc exp^mt тп^ 92 89 8. Плотность теплового потока в первом периоде N qI = rρ0 R 100 2880 3000 9. Продолжительность сушки во втором периоде до влажностей материала W = 10 и 5 % 1 , w10 тп=---In--- mK ^ 32 29 1 , Ws тп=--In--- 42 39 10. Плотности теплового потока во втором периоде сушки при влагосодержаниях материала W = 10 и 5 % qÏ = qI exp (- mtτÏ) 1297 1210 qÏ = qI exp (- mtτÏ) 1007 – бегая к построению и интегрированию кривой скорости сушки, рассчитать кинетику процесса. Этот метод позволяет при минимальном числе постоянных, определяемых из опыта, найти все основные параметры кинетики сушки — время сушки, температуру материала во втором периоде и интенсивность теплообмена, что значительно сокращает время и объем расчетной работы.

Полученные уравнения для вычисления m_t и m_u справедливы для группы влажных материалов, упрощают расчет параметров их сушки и значительно сокращают число экспериментов. Метод регулярного теплового режима может быть использован для обработки и анализа данных экспериментов по сушке разнообразных материалов при различных способах энергоподвода.