Исследование процесса теплопереноса в ограниченном пространстве

Введение. В современной боевой одежде пожарных (БОП) необходимо применять материалы и приспособления, обеспечивающие устойчивость к воздействию теплового потока плотностью не менее 5 кВт/м² в течение 240 секунд. Коэффициент теплопроводности пакета не должен превышать значение 0,06 Вт/(мК). В связи с этим возникла необходимость в исследовании теплотехнических характеристик устройства в ограниченном пространстве, когда перенос теплоты происходит за счёт свободной конвекции.

Цель исследования. Теоретическое изучение процесса теплопереноса в ограниченном пространстве и построение системы дифференциальных уравнений конвективного теплообмена.

Условия и методы исследования. Защитный пакет предназначен для повышения уровня безопасности пожарных при тушении очагов возгорания. При этом между промежуточными слоями боевой одежды устанавливается пакет, изготовленный из двух слоёв газонепроницаемого материала [1]. На одной стенке пакета закрепляются пружины, изготовленные из материала с памятью формы – нитинола. При повышении температуры окружающей среды слои одежды прогреваются. Пружины разворачиваются, создавая пространство между стенками пакета. Рассматриваются теоретические основы конвективного теплообмена применительно к движению среды в ограниченном пространстве.

Движение потока жидкости и газа происходит вследствие приложения внешних сил или при возникновении свободной конвекции [2]. В первом случае движение называется вынужденным – за счет насосов, вентиляторов, компрессоров, ветра и т.д. Во втором случае движение в поле земного тяготения возникает при неоднородной плотности среды и называется свободным.

В данной работе исследуется теплоотдача при свободном движении потока газа вблизи нагретой поверхности теплообмена. Температура стенки t _с принимается постоянной, т.е. t _с =const.

Особенности теплопереноса в ограниченном пространстве . Конвективный теплообмен происходит в вертикальной щели, образованной промежуточными слоями пакета. В зависимости от расстояния δ между стенками щели движение потока может развиваться различным образом. При достаточно больших значениях толщины δ около обеих стенок формируются не соприкасающиеся друг с другом пограничные слои. На горячей стенке, начиная с основания, возникает восходящий пограничный слой, на холодной – нисходящий. Отклонения от этой картины имеют место на концах щели. При малых значениях δ оба пограничных слоя взаимодействуют друг с другом, в результате чего в канале появляются циркуляционные контуры с высотой h (рис. 1).

а

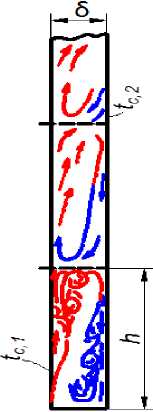
б

Рис. 1. Схема развития пограничных слоев: а – независимых; б – взаимодействующих

Высота контура зависит от толщины слоя, температуры стенок и физических свойств потока.

В первом случае расчёт теплообмена производится так же, как и для случая свободного движения около вертикальной пластины. С этой целью рассматривается аналитическое решение системы дифференциальных уравнений конвективного теплообмена.

Во втором случае расчет теплового потока производится с использованием уравнения теплопроводности ( ^Вт )

q =

^ ЗКв (t o 1 ^2 )

5         ,

где λэкв – эквивалентный коэффициент теплопроводности, Вт/(м K).

Для того чтобы дать рекомендации по расчёту теплообмена в щели данной конструкции слоя БОП, требуется формирование системы дифференциальных уравнений конвективного теплообмена.

Как всякое сложное явление, конвективный теплообмен имеет свои математические зависимости, характеризующие особенности процессов переноса теплоты и гидродинамики потока. При рассмотрении используются следующие допущения: среда однородна и изотропна, физические свойства постоянны, деформация объема отсутствует, перемещение среды происходит только в поле тяготения, а иные силы, оказывающие влияние на движение среды, отсутствуют [3].

Уравнение теплоотдачи. Его можно получить из уравнения теплового баланса в пограничном слое вблизи стенки: тепловой поток, передаваемый путем тепловодности через пограничный слой, равен тепловому потоку за счет конвективной теплоотдачи на границе стенка – поток я тепл=Qконв(2)

или

-λ( s )c = α Δt ,(3)

откуда

α=-λ(7 ) .(4)

Δt \dn .

Здесь λ - коэффициент теплопроводности , Вт/(м K); (^ ) - градиент температуры , ^К .

Для того чтобы знать распределение температуры вблизи стенки (  ) , надо использовать уравнение энергии.

Уравнение энергии. Используем I закон термодинамики для потока жидкости или газа dQ =dH+md(ω ) + dLтех,                             (5)

где      ԁН- изменение энтальпии,     Вт;     m

–

массовый     расход,

кг

; с

( ^ω )- изменение кинетической энергии , ^Дж ; dL _тех – техническая работа потока, Вт.

Анализ этого уравнения приводит к выводу: скорость значительно не изменятся, поэтому можно пренебречь изменением кинетической энергии, т.е. d( ^ω )=0 ; в потоке не установлен ротор, и техническая работа не совершается, т.е. d L _тех =0 .

Тогда dQ=dH , т.е. тепловой поток равен изменению энтальпии.

В свою очередь, dQ складывается из теплового потока за счет конвекции и теплопроводности

dQ = dQ конв +dQ тепл .

Тепловой поток dQ _конв = dm Δһ, где Δһ – изменение удельной энтальпии, Дж/кг; Δһ= һ- һ о, в свою очередь, һ о – энтальпия при t=0℃ , принимается как начало отсчёта энтальпии һ о =0.

Так как һ= сp t, то dQконв = dm сpt, =d(ρωdf)сpt= ρωcptdf.

Пользуясь преобразованием Остроградского-Гаусса, можно записать dQконв = - div (ρωcpt)dv.

Тепловой поток за счёт теплопроводности dQтепл = -λ ( ^ ) df = -λ[- div (^ ) ]dv.

\vll/ QQ

Изменение энтальпии равно dH = dm дт = ρdvc P дт = ρc P дт dv.(10)

После подстановки всех составляющих в уравнение I закона термодинамики для потока можно получить dt dt dt dt zd2t   d2t .д

τ x av+ωУ   +ωX   =(   +    +   ),(11)

τ или

5 =a∇2t .(12)

Здесь – полная или субстанциональная производная от температуры; a – коэффициент температуропроводности, м² /с.

Для решения этого уравнения необходимо знать поле скорости вблизи стенки, поэтому следует использовать уравнение движения.

Уравнение движения . Получим уравнение с учетом подъемной силы.

Пусть на бесконечно малый элемент потока объемом dV и площадью df действует ряд сил, вызывающих движение: dF _дав – сила давления; dF _тр – сила трения; dF _под – подъемная сила; dF _тяж – сила тяжести (рис.2).

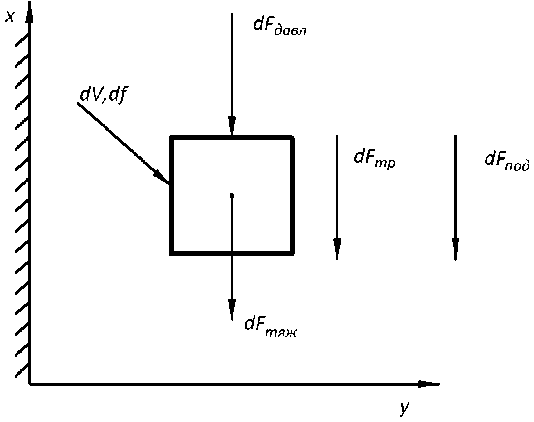
Рис. 2. К выводу уравнения движения

Равнодействующая всех сил равна сумме приложенных сил dFрав = dFдав + dFтяж - dFтр - dFпод.(13)

Принимается движение одномерным в направлении оси х. Тогда для всех приложенных сил можно использовать следующие выражения:

dFдав =pdf=-divpdV=-fi dV ;(14)

dFтр =- μ " ω; df = +div(μ ~д ωг)dV ;(15)

dFтяж = ρgdV;(16)

dFпод = d(ρgβΔt f) = ρgβΔtdf = -ρgβΔtdV.(17)

Здесь μ - коэффициент динамической вязкости, Па ∙ с; β – коэффициент объёмного расширения, 1/К.

Равнодействующая всех сил равна массе, умноженной на ускорение dFрав = ρd ^Rω 2 ,(18)

где ^ω – субстанциональная производная, характеризующая изменение скорости по времени и координатам

Dωx _ 5ωX      ^ωx       ωx^

=    +ω    +ω    +ω .

τ              τ

Тогда для объема dV можно записать

D ω x       i ap .л л

τ      ρ ax+gx-ρоgxβΔt+v ω .(20)

Уравнение сплошности . Рассматриваемая задача относится к сплошной среде, поэтому необходимо уравнение сохранения массы или уравнение сплошности. Его можно получить из уравнения массового баланса: изменение массы в объёме равно притоку (оттоку) массы, то есть

• 5 ρГ = ρωdf = - div(ρω)dv,

или dρ   d (ρω X)   d (ρω у)   a (ρωz)=0.(22)

dτ

Здесь τ – время,с.

Для стационарных задач ~dρ =0, и при ρ = const уравнение упрощается d- ω2+ -ω2+ d- ω2=0.(23)

dx dy dz

Для решения системы уравнений необходимо знать условия однозначности, то есть физические свойства потока жидкости или газа, геометрические характеристики теплоотдающей поверхно- сти, начальные распределения температуры для нестационарных задач, а также граничные условия, определяющие теплообмен на границе стенка–поток [4].

Выводы

• 1.    Для исследования конвективного переноса теплоты в защитном пакете в системе дифференциальных уравнений произведён учёт подъемной силы, возникающей при свободном движении потока.

• 2.    Для решения системы дифференциальных уравнений необходимо использовать условия однозначности конкретного случая теплообмена, позволяющие определить коэффициенты теплоотдачи и величины тепловых потоков.