Исследование процесса торможения двухколесного транспортного средства в сложных дорожных условиях

Безопасность дорожного движения является одной из актуальнейших задач современного автомобилестроения. Особое внимание при этом уделяется процессу торможения в сложных дорожных условиях, когда низкий коэффициент сцепления между колесом и дорогой приводит к блокировке колес, а значит не только к увеличению величины тормозного пути, но и к неизбежной потере управляемости автомобиля. Единственным решением этой проблемы является применение специальных антиблокировочных систем, контролирующих давление в тормозных магистралях для предотвращения блокировки колес. Однако если для современных автомобилей наличие антиблокировочной системы является обязательным, двухколесные транспортные средства (мотоциклы) достаточно редко оснащаются подобными устройствами.

Цель данной работы: изучение процесса торможения двухколесного транспортного средства и выявление зависимости величины тормозного пути от приложенного тормозного момента.

Описание процесса торможения двухколесного транспортного средства. При торможении двухколесного транспортного средства (ДТС) на эффективность этого процесса влияет большое количество факторов, однако одним из основных параметров является величина проскальзывания между колесом и дорожным покрытием, приводящая не только к увеличению тормозного пути, но и к потере управляемости [1,2]. Эта величина количественно оценивается скольжением и определяется следующим образом:

где v ДТС - абсолютная скорость двухколёсного транспортного средства, v _колёс - приведенная скорость колеса, определяемая как произведение величины его угловой скорости на радиус.

Для предотвращения проскальзывания и обеспечения режима торможения, близкого к оптимальному, применяются различные анти-блокировочные системы, принцип действия которых основан на изменении тормозного момента (фактически – силы прижатия тормозных колодок) в зависимости от величины скольжения. Обычно в двухколесных транспортных средствах абсолютная скорость не измеряется непосредственно, а определяется как произведение угловой скорости заднего колеса на его радиус. Таким образом, скольжение фактически определяется разностью угловых скоростей переднего и заднего колес [3-5]. Для исследования процесса торможения и формирования оптимальных законов управления рассмотрим модель, состоящую из одного колеса, соединенного с корпусом, который представим в виде сосредоточенной массы (рис. 1). Таким образом, расчетная схема состоит из трех тел: 1 – передного колеса m 1 , 2 – корпуса вместе с водителем m 2 , 3 – тормозного диска и тормозной колодки, массы которых не учитываются, 4 – заднего колеса.

Запишем дифференциальные уравнения движения системы:

5 =

v ДТС    v колёс

x 100%

v ДТС

m 2 ^X =- ^R 2, ^{+ F}TP 21

Туладхар   Даниел,   аспирант. E-mail: tuladhar2001

Подставляем уравнение (2) в (3) получим

m, x = - m 2 x - Ftp ,

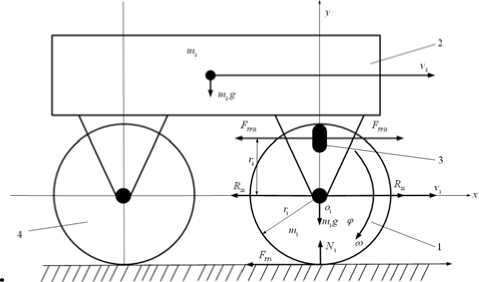
Рис. 1. Расчетная схема транспортного средства во время торможения:

N 1 – нормальная реакция переднего колеса ДТС, m 1 g 1 – сила тяжести, F TP 1 – сила трения переднего колеса, r ₁ – радиусы переднего колеса, r ₂ – расстояние от центра колеса до средней линией тормозной колодки, F_{TP 21} – сила трения между колодкой и тормозным диском, R x 21 – сила реакций, O 1 – центр массы колеса.

Условия проскальзывания можно выразить следующим образом:

F tp 1 >  f • N

где fN=F*TP, F*TP – максимальная величина силы трения.

Из (5) получаем, что при отсутствии проскальзывания FTP 1 = m2x тогда условие проскальзывания примет вид:

m ₂ x >  f • N

Связь между обобщенными координатами при отсутствии проскальзывания представим в виде x = φr . Тогда уравнение (5) преобразуется в вид:

^ Л ^m + ^m 2 ) = - F_T p ,

Обозначаем M TP 1 = F TP 1 r 2 и преобразим уравнение (4) к виду:

J = - M 1 + F TP 1 Г      (9)

Выразив силу трения из (8) получаем

ф(J + r(m + m 2)) =- MTP 1

• •           • •

x = ф • r1

Данная система описывает движение колеса без проскальзывания. Условием перехода к режиму движения с проскальзыванием служит неравенство (7). При движении с проскальзыванием сила трения принимается известной и равной ± F^* TP При движения с проскальзыванием система описывается следующими уравнениями:

x( mx + m 2) = FTP 1

F = f-N

TP 1

Условия перехода к решению движения без проскальзывания при этом имеет вид:

• •          • • x = ф-r

Для решения разработанной математической модели колеса предлагается алгоритм, представленный на рис. 2.

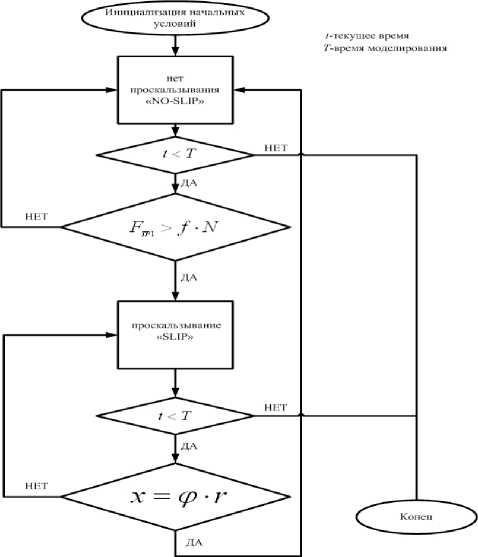
Рис. 2. Алгоритм численного решения математического модели

В алгоритме используются два блока: в блоке «NO SLIP» реализуется система уравнений (9), в блоке «SLIP» - система уравнений (10). Переход от одного блока к другому осуществляется по условиям (8) и (11). При решении использовался метод численного интегрирования Эйлера с постоянным шагом интегрирования.

Результаты моделирования. Графики, полученные в ходе моделирования движения системы, представлены на рис. 3.

На рисунке 3 (a) показан процесс торможения ДТС при тормозном моменте, равном 2 Нм. По рисунку видно, что полная остановка ДТС происходит за 3.4 с, при этом тормозной путь составляет 110 м. На рисунке 3(b) тормозной момент увеличен до 3 Нм и полную остановку ДТС произошла за 2 с, при этом тормозной путь сократился и составил 75 м. На рисунке 3(c) тормозной момент составляет 4 Нм и полная остановка происходит за 4 с, при этом тормозной путь равен 115 м. Во время торможения при тормозном моменте равном 2 Нм мы видим, что угловая скорость и скорость движения изменяются пропорционально и проскальзывания не происходит. При увеличении тормозного момента до 3 Нм время торможения уменьшается, при этом также не происходит проскальзывания между колесом и дорогой. Дальнейшее увеличение тормозного момента до 4 Нм, приводит к возникновению проскальзывания, при этом колесо блокируется и остановка происходит за счет трения скольжения между колесом и дорожным покрытием, время полной остановки при этом увеличивается и, при дальнейшем увеличении тормозного момента, остается постоянным.

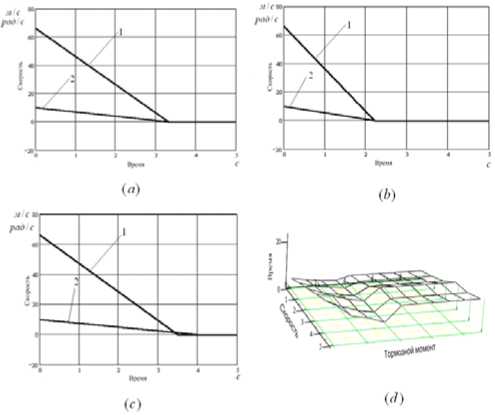
Рис. 3. Процесс торможения переднего колеса ДТС : 1 – угловая скорость колеса , 2 – скорость движения ДТС

На рисунке 3(d) представлен трёхмерный график, иллюстрирующий зависимость между начальной скоростью, временем остановки и тормозным моментом при постоянном коэффициенте трения. По графику видно, что при величине тормозного момента, равной 3 Нм, время торможения минимально и при этом не происходит проскальзывания колеса. Таким образом, управление величиной тормозного момента может значительно повысить эффективность торможения и сократить время остановки.

Выводы: на эффективность процесса торможения, а в конечном счете и на величину времени остановки, помимо тормозного момента, оказывает влияние и степень проскальзывания между колесом и дорогой. Так, при блокировке колеса дальнейшее увеличение тормозного момента не оказывает никакого эффекта. Таким образом, оптимальной можно считать величину тормозного момента, которая является максимально возможной при условии отсутствия проскальзывания. Целью дальнейшего исследования является определение эффективности различных алгоритмов управления тормозным моментом, основанных на измерении величины скольжения.