Исследование процессов конвергенции и депопуляции в системе центр-периферия

Результаты математического модели‑ рования социально–экономических про‑ цессов используются как в сфере государ‑ ственного управления и стратегического планирования, так и в крупном бизнесе [1–3]. При этом запрос современного обще‑ ства сфокусирован на концепции «устой‑ чивого развития», которая сталкивает‑ ся с рядом вызовов1. В частности, серьёз‑ ной проблемой, препятствующей устой‑ чивому развитию, является демографи‑ ческий переход, обусловленный увеличе‑ нием продолжительности жизни людей, изменением их образа жизни, и связанное с этим старение населения. Эти факто‑ ры в совокупности приводит к новым со‑ циально‑экономическим и медицинским проблемам (в том числе к росту угроз гло‑ бальных пандемий, увеличению риска по‑ явления новых или возврата исчезнувших инфекций).

Важность демографии и сопряжённых с ней изменений в социальной жизни об‑ щества признаётся как у нас в стране, так и во всем мире [4]. Соответственно, появ‑ ляется актуальная научная задача по мо‑ делированию динамики роста народо‑ населения с учётом социально‑экономи‑ ческих факторов. Анализ миграционных потоков сам по себе является многофак‑ торной задачей, во многом зависящей от исторического контекста. Так, для эпохи появления человечества, помимо очевид‑ ного градиента населённости и существо‑ вавших географических, климатических и иных внешних причин, важным факто‑ ром считается генетическая предрасполо‑ женность к поиску новизны [5]. Возникно‑ вение цивилизаций, пассионарность эт‑ носов, как движущая сила не только ми‑ грации, но и экспансии [6], принимающей формы военных действий или культур‑ ного проникновения, все ещё продолжает центробежную тенденцию миграционных потоков. Однако, уже в эпоху географиче‑ ских открытий и колонизации возникает и противоположный поток, «восходящая диффузия» [7]. Метрополии становятся центром притяжения для мигрантов, не всегда добровольного [8; 9]. Центростре‑ мительные тенденции мотивируются раз‑ ницей условий жизни, которые включают уровень доходов, доступность и качество образования, социальную защищённость, возможности самореализации и так далее. Тема изучения влияния демографических изменений на экономику стран становит‑ ся особенно актуальной в периоды актив‑ ных социально‑экономических и поли‑ тических изменений (например, [10] или крупное статистическое исследование Goldman Sachs «Азианомика в Америке: вклад и вызовы»2).

В настоящей работе предложено раз‑ витие стратовой демографической моде‑ ли, характеризующейся наличием двух условных страт (мегарегионов), отличаю‑ щихся образом жизни, уровнем развития и ценностными установками. В рамках модели используются обозначения Центр и Периферия, подчеркивающие роль этих страт как институциональных ловушек, определяющих демографические и эко‑ номические показатели групп стран и на‑ селения. Исходная стратовая модель [11] была дополнена некоторыми предположе‑ ниями модели великой дивергенции/кон‑ вергенции Коротаева [12].

Основные уравнения модели

Пусть X ( t ) описывает численность населения условной страты Центр, а Y ( t ) — численность страты Периферия. Определим относительные (без

XY размерные) величины как, x = —,у = — X0    Y0

где Xo = X(0) и Yo = Y (0) — численности населения в начальный момент времени. Тогда их динамика может быть описана системой дифференциальных уравнений [13]:

dx            Y dy

— = ax - dx ² + w — и y ayay - dy ² - w (1)

dt ^xx X₀ и dt ^yy ( )

Здесь первые два слагаемых в правой части уравнений отвечают за логистиче‑ ский рост населения в стратах, определяя естественный прирост населения (раз‑ ность между рождаемостью и смертно‑ стью) в момент t . Третье слагаемое с ко‑ эффициентом w отвечает за миграцию (пе‑ реток между стратами). Поскольку модель двухкомпонентная, то миграционные по‑ токи сохраняют общий размер популя‑ ции, следовательно, и знаки этих слагае‑ мых должны быть противоположны, а для использования безразмерных величин нужно учесть, что относительное измене‑ ние населения Центра на одного мигран‑ та будет иметь фактор Y0/ X0 по отноше‑ нии к Периферии. В отсутствие миграции (w = 0) каждая из систем следует логистической кривой с насыщением, определяе‑ мым отношениями аа /dа , а = x,у [13].

В определённом приближении показа‑ тель доли ВВП на душу населения может служить количественным ориентиром для оценки направления (знака w в (1))

и интенсивности миграционных потоков. Однако, при наличии существенного не‑ равенства, желательно использование по‑ казателей, лучше отражающих уровень жизни возможно более широкого слоя гра‑ ждан, например, медианного дохода. Кро‑ ме того, желательна корректировка этой величины с учётом паритета покупатель‑ ной способности и «прожиточного мини‑ мума». Тогда, в рамках предлагаемой мо‑ дели миграция:

А Г S x " S y ) _ xy_ X_n S + S I x ² + 1

⁰ V ^x у )

где S_x , S_y — величина дохода на душу населения (с учетом сказанного выше) в стратах Центр и Периферии, соответ‑ ственно; A — коэффициент нормировки миграционного потока.

Например, следуя [12], можно считать, что соотношение и динамика доходов определяются из решения уравнений сле‑ дующего вида [5]:

dS x = b S dt xx

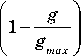
dS

—y = b S dt yy

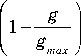
и    g = x ( m + S x ) + у ( m + S y ) ,      (3)

где b_x и b_y — коэффициенты роста дохо‑ да, g и g _max — суммарный доход на душу населения и его предельная величина, m — сумма «прожиточного минимума» [12; 14]. Более точная модель может учитывать пе‑ ретекание доходов вместе с миграционны‑ ми потоками в зависимости от оценки от‑ носительной экономической активности мигрантов. Однако, в настоящей работе мы ограничимся рассмотрением достаточно простых сценариев экономического роста, сосредоточившись на исследовании дина‑ мики численности населения.

Общие для различных сценариев пара‑ метры, используемые в дальнейшем в ма‑ тематическом моделировании, выбраны следующими:

a = 0.1, a = 0.1, d = 0.0095, d = 0.005 xy xy ,

Y ₀ / X ₀ = 0.2, A = 0 ^ 0.1 .

Без учёта миграции они соответству‑ ют растущим популяциям как Центра, так и Периферии, однако мы предполагаем, что страта Центр находится существен‑ но ближе к насыщению на логистической кривой, именно этим обусловлен выбор численных значений параметров. Специ‑ фические значения параметров при ис‑ пользовании логистической модели дол‑ жны быть выбраны из соображений со‑ впадения наблюдаемой динамики иссле‑ дуемых систем на основе доступных ста‑ тистических данных с ходом рассчитан‑ ных траекторий переменных x и y до настоящего момента.

В качестве модельной ситуа‑ ции будем предполагать устойчи‑ вый экономический рост страты Центр с темпом в, который будем считать постоянным: Sx = Sx (0)exp (рt). Это предположение не уменьшает общность моде‑ ли, поскольку важными для миграцион‑ ных процессов являются относительные величины и их динамика, а уровень дохо‑ дов Центра достаточно сильно коррелиро‑ ван с глобальным для Системы уже бла‑ годаря большей доли экономики центра в ВВП Системы. Для страты Периферия мы рассмотрим модель конвергентного роста, когда существенный разрыв в уров‑ не доходов между Центром и Периферией в начальный момент времени экспонен‑ циально сокращается с характерным вре‑ менем τc экономической конвергенции:

t

т

c

S = S -ДS exp yx

Соответствующие иллюстрации приве‑ дены на рис. 1, где продемонстрировано сближение уровней дохода в стратах Центр и Периферия в зависимости от ве‑ личины характерного времени конверген‑ ции τ _c . Параметры экономической кон‑ вергенции Центра и Периферии выбраны следующими: Д S / S x ( 0 ) = 0.5 , P = 0.02 , t c = 5 +30 .

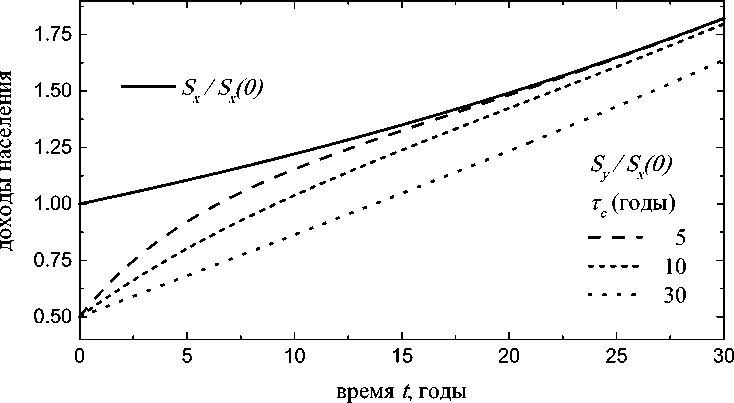
Рис. 1. Сближение уровней дохода в стратах Центр и Периферия в зависимости от величины характерного времени конвергенции τ _c (сплошной линией показан нормированный доход Центра, пунктиром — нормированный доход Периферии для разных времён конвергенции)

Fig. 1. Convergence of income levels in the countries of the Center and the Periphery depending on the value of the characteristic convergence time τ _c (Solid line corresponds to normalized Center income dynamics, dashed lines — normalized Periphery income dynamics for various convergence times)

Источник: рассчитано авторами для модельной системы (1)‑(3).

Результаты математического моделирования и их обсуждение

Численные расчёты в соответствии с моделью показывают, что при от‑ сутствии экономического сближения (тc ^ да ) Периферия испытывает устойчивый миграционный отток, который при выбранных параметрах демографической модели не компенсируется естественным приростом населения и достаточно бы‑ стро приводит к депопуляции Периферии. При этом, в силу большей близости Центра к насыщению в демографической модели, миграционный приток в Центр фактиче‑ ски «растворяется», а при существенной депопуляции Периферии перестаёт ком‑ пенсировать естественную убыль населе‑ ния Центра, что может привести к депо‑ пуляции всей Системы Центр‑Периферия.

Изменение этой тенденции требует сближения Sy и Sx , причём, за характер‑ ное время τc существенно меньшее, чем характерные времена демографических изменений. Отметим, что наличие пара‑ метра ∆S отражает концепцию догоняю‑ щего развития, когда Периферия функ‑ ционирует в той же системе ценностей, что и Центр. (рис. 2). Из приведённых ил‑ люстраций видно, что Периферии нужно достаточное время (порядка 2τc ) для вы‑ хода из режима снижения численности и возвращения к траектории роста населе‑ ния. Поскольку на временах, значительно превышающих τc , заметно меняются па‑ раметры системы, что на практике соот‑ ветствует демографическому переходу, качественной смене состояния системы, предложенная модель не может быть уни‑ версальной и не претендует на описание демографической динамики на длинных временных интервалах.

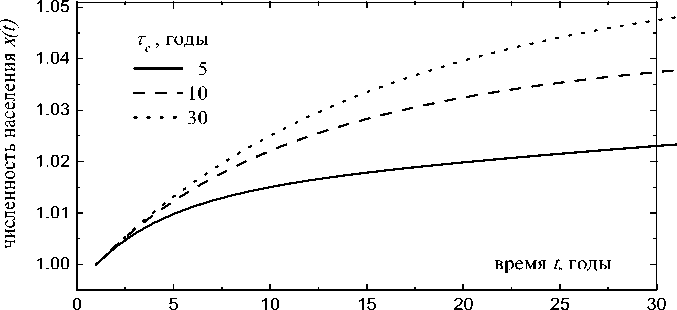
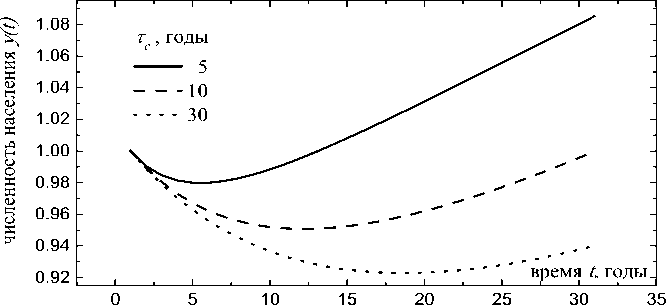
Рис. 2. Динамика численности населения Центра

X ( t ) и Периферии для различных величин ^т c

Fig. 2. Population dynamics of the Center x(t) and the Periphery y(t) for various values of τ _c

Источник: рассчитано авторами для модельной системы (1)‑(3).

Устойчивое развитие (sustainable development) должно включать и решение общечеловеческих проблем в рамках гло‑ бальных договорённостей, таких как кон‑ троль изменений климата или распро‑ странения заболеваний3, что также прак‑ тически невозможно без полноценного участия стран Периферии. Поток рабочей силы из Периферии до определённой сте‑ пени позволяет решать, как проблему не‑ достатка высококвалифицированных спе‑ циалистах в определённых областях, так и вопрос поддержания сравнительно низ‑ кого уровня оплаты труда, не требующе‑ го высокой квалификации, в частности в сельском хозяйстве и секторе услуг. Од‑ новременно подавляются потенциальные центры конкуренции и расширяются рын‑ ки сбыта. В то же время, всё чаще возника‑ ет вопрос, насколько такая модель может быть устойчивой, не приводит ли она к ка‑ тастрофическим изменениям демографи‑ ческих и экономических перспектив Пе‑ риферии, нарастанию политических про‑ блем, что, в свою очередь, может вызвать уже неконтролируемые процессы мигра‑ ции, разрушительные не только для Пери‑ ферии, но и для Центра.

Таким образом, может быть оправдан‑ ным экономическое участие стран Цен‑ тра с целью добиться устойчивого эконо‑ мического сближения. Ещё раз отметим, что вопрос равномерности доходов — важ‑ ный фактор «качества» роста и его влия‑ ния на миграцию. Именно поэтому рост должен быть связан с достаточно мед‑ ленной перестройкой структуры эконо‑ мики и развитием общественных инсти‑ тутов и не может быть обеспечен едино‑ временным «вливанием». С разной сте‑ пенью эффективности могут предприни‑ маться различные шаги в этом направле‑ нии — от прямой экономической помощи или государственных заимствований до многоуровневой кооптации, включающей интеграцию в финансовую и экономиче‑ скую систему, доступ к рынкам капитала, создание высокооплачиваемых рабочих мест путём организации современного производства, развитие потребительско‑ го рынка, долгосрочные инфраструктур‑ ные проекты, вложения в науку и образо‑ вание. Надо отметить, что экономическая помощь Центра зачастую обуславливает‑ ся требованиями структурных реформ и/ или политической интеграции, что может восприниматься со стороны Периферии как угроза суверенитету (не всегда бес‑ почвенно). В результате может возникать «замкнутый круг», когда получение и эф‑ фективное использование помощи Центра затруднительно без проведения реформ, а экономическая ситуация делает подоб‑ ную попытку политически невозможной.

По мнению авторов, для анализа демо‑ графической динамики может быть при‑ менена концепция институциональной ловушки [15], когда возникает невозмож‑ ность изменения динамики системы вви‑ ду существующих институциональных (правовых, моральных и других) ограни‑ чений. На практике это выражается в том, что попытки резкого слома существую‑ щих практик (экстраординарные подхо‑ ды) приведут к радикальному изменению социальной ткани общества, а отказ от реформ приводит к институциональной диффузии, деструкции базовых инсти‑ тутов текущих социального и экономи‑ ческого порядков. Фактически, это озна‑ чает отсутствие однозначно «хороших» решений.

На языке математических моделей этим ситуациям отвечает в первом случае резкое изменение параметров (новые за‑ коны и запреты) при сохранении началь‑ ных условий, а во втором — изменение на‑ чальных условий (таких переменных как численность разных страт). Отметим, что существующие на сегодня количествен‑ ные методы оценки неустойчивости си‑ стем (показатели Ляпунова, размерности системы) могли бы позволить выбрать та‑ кое изменение параметров, которое не приведет к разбалансировке системы, ис‑ ключит ее переход в хаотическое (или не‑ устойчивое) состояние. Представляется, что, несмотря на свою трудоемкость, эти исследования могут быть реализованы в будущем при наличии заинтересован‑ ности со стороны власти или представи‑ телей бизнеса.

Выводы

Предложенная модель позволяет оце‑ нить, насколько экономическое сближе‑ ние создаёт демографическую (миграци‑ онную) конвергенцию Центра и Перифе‑ рии. Фактор времени ( τ _c ) является крити‑ ческим в вопросе, сможет ли страта Пери‑ ферия за счёт опережающего экономиче‑ ского роста в достаточно обозримой пер‑ спективе (5–15 лет) выйти на уровень, ко‑ гда миграционный отток не превышает естественный прирост населения. В про‑ тивном случае наблюдается устойчивая необратимая депопуляция Периферии, причём Центр, находясь, как мы предпо‑ ложили, ближе к насыщению, фактически «растворяет» миграционный поток без су‑ щественного демографического эффекта.

Надо отметить, что в случае успешной экономической конвергенции страты Пе‑ риферия и быстрого восстановления чис‑ ленности населения модель выходит за область применимости, так как демогра‑ фические параметры такой страты дол‑ жны изменяться, также приближаясь к со‑ ответствующим значениям для Центра. Понятно, что определённая специфика Периферии при этом может сохраняться: возрастной состав, образовательный уро‑ вень и другие параметры изменяются бо‑ лее медленно, чем экономика; так что та‑ кая экстраполяция выходит за рамки на‑ шего рассмотрения.

Отметим, что фактор времени является принципиально важным в демографиче‑ ских моделях. Во‑первых, имеет место суще‑ ственная необратимость демографических процессов, приводящая к «стреле времени» и в социальных процессах. Это выражается, в частности, в сложности изменения мигра‑ ционных правил (легко принять мигрантов, тяжело их исключить из социума, не прибе‑ гая к экстраординарным методам) или де‑ мографических установок (отмена китай‑ ского подхода «одна семья — один ребёнок» не привела к росту рождаемости). В нашем случае это означает невозможность про‑ извольного изменения параметров систе‑ мы: происходит «наследование» состояний, и новые значения коэффициентов (рождае‑ мость, смертность, коэффициент миграции и пр.) не могут резко изменить предыдущие тренды. Это отражает ригидность демогра‑ фических систем (их «грубость» в термино‑ логии В. И. Арнольда [16]). Во‑вторых, в по‑ добных задачах важным оказывается учет времени запаздывания: принятые решения не могут быть моментально отражены в си‑ стеме, результат их воздействия отсрочен.

Дальнейшее развитие предложенной модели может заключаться в исследо‑ вании иных сценариев экономического взаимодействия, а также в учёте демогра‑ фических и миграционных параметров в уравнениях экономического роста. От‑ дельным интересным вопросом должна стать социально‑экономическая интер‑ претация полученных результатов и раз‑ работка на их основе предложений по оп‑ тимизации управленческих решений.