Исследование процессов взаимодиффузии в тонких прозрачных средах методами лазерной интерферометрии

Явление массопереноса и диффузионные процессы в различных средах имеют важное практическое значение для разработки регламентов технологических процессов, анализа и разделения веществ и т.п. Набухание и растворение, пленко- и волокнооб-разование, адгезия, ликвация и адресная доставка лекарственных препаратов – вот далеко не полный перечень процессов, в которых диффузия компонентов играет основополагающую роль.

Для изучения диффузионного транспорта применяют различные физико-химические методы. Особое место среди них занимают оптические методы [1,2], в частности, интерференционные, обладающие высокой чувствительностью и позволяющие следить за кинетикой массопереноса в режиме реального времени [1-4]. Для бинарных систем по данным интерференционного эксперимента определяют профили распределения показателя преломления, концентрации, рассчитывают коэффициенты взаимо-диффузии компонентов в широкой области составов и температур, строят фазовые диаграммы, оценивают термодинамические параметры [5-8].

Применение результатов интерференционных исследований весьма обширно. Так, данные интерферометрии позволяют не только с высокой надежностью определять пограничные кривые, но и идентифицировать тип фазового разделения и, соответственно, прогнозировать структурно-морфологические особенности и кинетическую устойчивость получаемых материалов (пленок, покрытий, волокон, пластмасс и др.), а также их характеристики при эксплуатации в различных условиях [9-11]. Результаты интерферометрии применяют при моделировании процессов нанесения и сушки покрытий, деструкции полимеров в различных средах и др. [4,6]. В последнее время отмечается тенденция к расширению применения интерференционных методов исследования в таких областях, как биохимия и фармакология [12-14]. В [13] исследованы процессы массопереноса и растворимости лекарственных препаратов в полимерных матрицах методом многолучевой интерферометрии, а в [14] показано, что интерферометрический метод может успешно применяться для изучения биодеградации полимеров.

В настоящей работе приведены результаты исследований методами лазерной интерферометрии процессов массопереноса в бинарных системах полимер + низкомолекулярная жидкость и низкомолекулярная жидкость I + низкомолекулярная жидкость II.

Оптическая интерферометрия фазовых объектов

Прозрачные среды с пространственными вариациями геометрической толщины d ( x , y , z ) или/и показателя преломления n ( x , y , z ) относятся к классу фазовых объектов, поскольку изменяют (пространственно модулируют) фазу прошедшей через них волны. Параметры зависимостей d ( x , y , z ) , n ( x , y , z ) и, в целом, оптической толщины объекта D ( x , y , z ) = d ( x , y , z ) ■ n ( x , y , z ) можно определить с помощью оптического интерферометра [15-20].

Для исследования параметров фазовых объектов методом оптической интерферометрии используют как классические [15-19], так и голографические [20-23] интерференционные системы. Классические системы в основном базируются на двулучевых интерферометрах Маха-Цендера и многолучевом интерферометре Фабри-Перо.

Для определения параметров фазового объекта методом классической оптической интерферометрии его помещают в пучок света в плечо интерферометра. Прошедшая через объект световая волна приобретает дополнительную пространственную фазовую модуляцию AV(x, y), определяемую пространственными вариациями оптической толщины объекта D (x, y, z). В выходной ветви интерферометра объектная волна интерферирует с опорной волной, и образуется картина интерференционных полос с пространственным распределением интенсивности I(x, у) [16-18]:

I (x, у ) = Is + IR +

^{S R} , (1)

+ 2 V I s ¹ » cos [AT о ( x , У ) + AT ( x , У ) ]

где I_S и I_R – интенсивности объектной и опорной волн, AT ₀ ( x , у ) - начальная разность фаз объектной и опорной волн.

Форма интерференционных полос, их пространственное расположение и пространственный период определяются начальной разностью фаз AT ₀ ( x , у ) и дополнительной фазовой модуляцией объектной волны AT ( x , у ) . Если начальная разность фаз постоянна по всему сечению выходного поля, AT ₀ ( x , у ) = T ₀ = const , то интерферометр работает в режиме полос бесконечной ширины. Для режима полос конечной ширины создают начальную разность фаз AT ₀ ( x , у ) , как правило, в виде линейной зависимости от координаты, AT ₀ ( x , у ) = ( 2 л/Х ) а у , где X -длина волны; а - угол взаимного наклона волновых фронтов полей. В этом случае на выходе интерферометра наблюдаются прямолинейные интерференционные полосы с периодом Л ® X/а , перпендикулярные оси Y , которые также называют опорными полосами.

В ряде случаев по картине интерференционных полос I ( x , у ) можно непосредственно определить фазовую модуляцию AT ( x , у ) объектной волны, а затем и оптическую толщину объекта D ( x , у , z ) . Следовательно, при известной зависимости d ( x , у , z ) можно определить пространственное распределение показателя преломления n ( x , у , z ) исследуемого объекта. Наиболее просто такая обратная задача решается для тонких квазиплоских фазовых объектов, для которых имеют место только зависимости d ( x , у ) и n ( x , у ) . Для тонких объектов с известной постоянной толщиной d = const распределение показателя преломления n ( x , у ) определяется практически непосредственно по форме интерференционных полос.

Для несимметричных распределений показателя преломления в объемных фазовых объектах используют метод голографической интерферометрии с применением диффузного рассеивателя для обеспечения многонаправленного зондирования объемного объекта [20-23]. Кроме этого, голографический метод, как дифференциальный метод контроля, позволяет исследовать быстропротекающие процессы и среды со сложным распределением показателя преломления в резервуарах с окнами неоптического качества. Трехмерное распределение показателя преломления можно определить и с помощью методов оптической интерференционной томографии, в которой также используется многонаправленное зондирование исследуемого объекта [24].

Интерферометр Маха-Цендера

Наиболее часто для исследования тонких фазовых объектов применяют интерферометр Маха-Цендера [16-18]. Фазовый объект располагается в одном из плеч интерферометра. На выходе интерферометра располагается объектив для формирования действительного изображения плоскости сечения объекта. Картина интерференции объектной и опорной волн наблюдается в плоскости изображения объекта IP (рис.1).

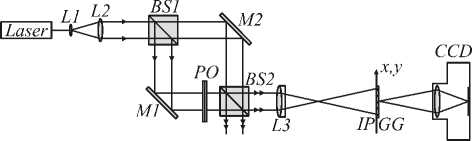
Рис.1. Схема лазерного интерферометра Маха-Цендера для изучения фазового объекта: L1 и L2 – линзы, составляющие коллиматор; BS1 и BS2 – делители пучков света; M1 и M2 – поворотные зеркала; PO – фазовый объект; L3 – объектив; IP – плоскость изображения объекта; GG – матовое стекло; CCD – ПЗС-камера

В наших экспериментах с интерферометром Ма-ха-Цендера в основном использовался He-Ne лазер с линейной поляризацией излучения. При использовании лазерного диода необходимо более точно выравнивать оптические пути в плечах интерферометра, поскольку излучение диода имеет существенно меньшую длину временной когерентности l_c «X 0 /AX , чем излучение He-Ne лазера. В интерферометре Маха-Цендера это выравнивание оптических путей выполнить достаточно сложно и неудобно даже при использовании прецизионных механических устройств.

На рис.2 показана интерферограмма фазового объекта – смеси полимера с растворителем в тонкой кювете. Интерферометр был настроен на полосы конечной ширины. Это позволяет определять знак изменения показателя преломления A n ( x , у ) .

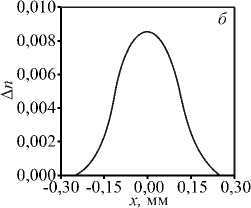
Рис. 2. (а) Интерферограмма процесса взаимодиффузии в системе ацетат целлюлозы-нитрометан в полосах конечной ширины (интерферограмма получена в интерферометре Маха-Цендера); (б) пространственное распределение изменения показателя преломления, реконструированное по интерферограмме

Для регистрации интерферограммы на выходе интерферометра использовался фотоаппарат NIKON Coolpix 4300. Цифровая интерферограмма подвергалась компьютерной обработке – контрастированию и сглаживанию спекл-модуляции изображения [25] для повышения точности определения положения центров интерференционных полос. Для расчета фазовой модуляции, вносимой объектом – полимером в среде растворителя, использовалось следующее выражение

Л^( x ) = 2П( n ( x )-n 0) d , (2)

где n ₀ – показатель преломления растворителя без полимерного волокна; n ( x ) - показатель преломления раствора полимера в растворителе; d - толщина плоского капилляра кюветы. Толщина капилляра d = 0,22 мм задавалась специальными металлическими спейсерами – калиброванной проволокой. Полагалось, что на прямолинейном участке каждой полосы ЛТ ( x ) = 0 ( n ( x ) = n ₀ ) . Значения ЛТ ( x )

определялись в точках x_j пересечения прямой x = const с центрами светлых и темных интерференционных полос. Таким образом определялись дискретные значения ЛТ ( x j ) , кратные п рад.

Решение уравнения (2) относительно n ( x ) при известных d , n ₀, X и установленных в эксперименте значениях ЛТ ( x j ) позволяет определить значения n ( x j ) , по которым интерполяционным путем можно определить профиль показателя преломления n ( x ) раствора полимера:

=    XW( x )

^{П ( j} ”0     2 п d

.

Кривая изменения показателя преломления, реконструированная по интерферограмме, представлена на рис.2б. Абсолютная погрешность реконструкции изменения показателя преломления составила, по нашим оценкам, 0,0003.

Интерферометр Майкельсона

Процесс массопереноса в системе диацетат целлюлозы – нитрометан исследовали на лазерном интерферометре Майкельсона. Схема экспериментальной установки приведена на рис.3.

В одно из плеч интерферометра устанавливали кювету PO с исследуемой системой. Объективы L3 и L4 использовались для формирования на CCD матрице (использовалась цифровая система ввода изображения VS-CTT-205) увеличенного изображения кюветы. В ходе эксперимента велась непрерывная запись кадров цифровых интерферограмм на жесткий диск компьютера. В качестве кюветы ис- пользовали две плоскопараллельные стеклянные пластинки, скрепленные между собой специальным зажимом. Зазор между пластинками устанавливали при помощи двух металлических спейсеров диаметром 210 мкм. Диаметр спейсеров измеряли микрометром и дифракционным методом.

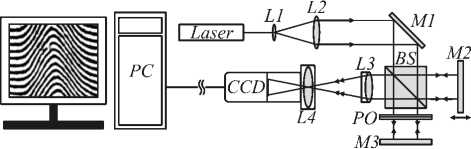
Рис.3. Схема экспериментальной установки на основе лазерного интерферометра Майкельсона, модифицированного для исследования малых фазовых объектов: L1 и L2 - коллиматор; BS – делитель пучка; PO – кювета с изучаемым фазовым объектом; M1 – поворотное зеркало; M2 и M3 – плоские зеркала интерферометра; L3 и L4 – объективы; CCD – камера;

PC – компьютер

Методика экспериментов с использованием лазерного интерферометра Майкельсона состояла в следующем. Образец ацетатного волокна помещали вертикально в воздушный зазор кюветы. Интерферометр путем прецизионного наклона зеркал M2 и M3 (рис.3) настраивали на горизонтальные полосы конечной ширины. Затем в зазор кюветы с волокном заливали растворитель. По изменению формы интерференционных полос наблюдали процесс растворения ацетата целлюлозы в нитрометане. Изменяющуюся картину интерференционных полос фиксировали ПЗС–камерой и вели непрерывную запись изображений с частотой записи кадров f = 0,5 Гц.

На рис.4 приведены интерферограммы, наблюдаемые на различных стадиях процесса растворения ацетатного волокна в нитрометане.

Рис.4. Эволюция интерференционной картины, наблюдаемой на выходе интерферометра Майкельсона в процессе взаимодиффузии компонентов системы ацетат целлюлозы–нитрометан: (а) t=1 мин, (б) t=2 мин, (в) t=5 мин, (г) t=10 мин, (д) t=15 мин, (е) t=20 мин, (ж) t=30 мин, (з) t=50 мин

На начальных стадиях процесса наблюдается резкоочерченное изображение волокна с изогнутыми интерференционными полосами и горизон- тальными полосами конечной ширины в области растворителя (рис. 4a). В волокне происходит достаточно интенсивное рассеяние света, поэтому его изображение выглядит темным с отчетливой пятнистостью (спекл-модуляцией), снижающей контраст полос в пределах изображения волокна (рис. 4а, б). Со временем в результате диффузии растворителя в полимер и массопереноса ацетата целлюлозы в растворитель, волокно становится более оптически однородным и в области его изображения контраст полос увеличивается (рис. 4б). В процессе дальнейшего диффузионного смешения в области изображения волокна формируются непрерывные полосы, претерпевающие характерный изгиб в зоне взаимодиффузии (рис. 4в-е). Ширина области изгиба полос со временем возрастает, что свидетельствует о расширении диффузионной зоны. Вместе с этим сглаживается пространственное распределение показателя преломления – уменьшается его градиент. В области локализации волокна показатель преломления со временем стремится к показателю преломления растворителя (рис. 4 ж-з).

Полученные цифровые интерференционные картины подвергались компьютерной обработке с целью увеличения контраста полос и сглаживания оптического шума – спекл-модуляции. Далее для каждой интерферограммы с учетом коэффициента увеличения в изображающей системы определялась пространственная фазовая модуляция объектного поля ЛТ ( x , t = const ) в горизонтальном направлении X (перпендикулярно волокну), вносимая диффузионным процессом.

Дискретные значения этой фазовой модуляции ЛТ m ( x j , t k ) = m п определяли по точкам пересечения оси X с центрами светлых и темных полос. Поскольку в интерферометре Майкельсона световая волна дважды проходит через фазовый объект, то переменная в направлении оси X составляющая фазовой модуляции определяется выражением

ЛТ( x/) = yt n ( xj)- n 0 ] d ,

где n ( x j ) - значение показателя преломления среды в капилляре кюветы в дискретных точках x_j , n ₀ – показатель преломления растворителя, d – толщина капилляра кюветы.

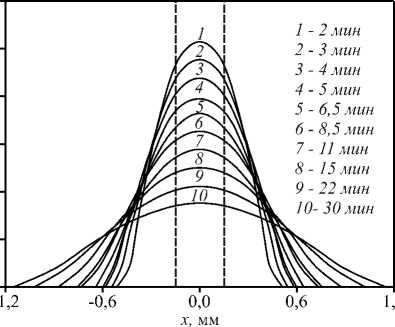
С использованием выражения (4) по значениям ЛТ _m ( x j , t k ) для каждого момента времени t_k рассчитывались значения изменения показателя преломления среды Л n ( x j , t k ) = n ( x j , t k ) - n ₀. На рис. 5 представлены зависимости изменения показателя преломления системы диацетат целлюлозы – нитрометан в процессе взаимодиффузии компонентов этой системы.

0,012

0,010

0,008

< 0,006

0,004

0,002

0,000

-                                                             2

Рис. 5. Пространственные распределения изменения показателя преломления Л n ( x ) в процессе взаимодиффузии компонентов системы диацетат целлюлозы – нитрометан. Вертикальными пунктирными линиями показаны первоначальные границы волокна

По кривым пространственного распределения изменения показателя преломления с использованием модели диффузии из бесконечно тонкого слоя в неограниченное тело [26] был рассчитан усредненный коэффициент диффузии диацетата целлюлозы в нитрометане, который составил D = 7 - 10^-7 см²/с. Погрешность определения коэффициента диффузии составила, по нашим оценкам, не более 10%.

Исследование массопереноса компонентов в модельной системе диацетат целлюлозы–нитрометан весьма перспективно, поскольку позволяет оценить возможность применения классических интерференционных схем для исследования взаимодиффу-зии компонентов в системе высокомолекулярное вещество (полимер) – низкомолекулярная жидкость (растворитель). Кроме того, разработанные подходы (применение увеличительной оптики и др.) могут быть применены в исследовании влияния природы низкомолекулярного вещества, молекулярной массы, молекулярно-массового распределения и структурно-морфологических особенностей высокомолекулярного компонента на диффузионные характеристики других практически важных систем полимер– низкомолекулярная жидкость (растворитель, осадитель, пластификатор), широко используемых в технологии получения пленок, мембран, полых волокон, разнообразных фармацевтических форм пролонгированного лечебного действия и др.

Исследование процессов биодеградации полимера

Термические ожоги кожи являются одними из самых распространенных травм как на производстве, так и в быту. Одним из перспективных подходов к лечению термического поражения кожи является использование пленочных покрытий на основе биодеградирующих (рассасывающихся) полимеров. Преимущества таких покрытий заключаются в том, что, с одной стороны, они выполняют защитную функцию, закрывая рану от внешнего инфицирования, и обладают бактерицидными свойствами, а с другой – могут выполнять лечебную роль, участвуя в развитии различных репарационных процессов [27]. В основе способности этих материалов к биодеградации лежит водо- и плазморастворимость, исследование которой in vivo классическими методами связано с рядом трудностей. В связи с этим разработка других методов и подходов к оценке сорбционно-диффузионных параметров процесса «биодеградации» полимера представляется актуальной задачей.

В рамках настоящей работы исследована возможность применения метода лазерной двулучевой интерферометрии для исследования процессов биодеградации пленочных материалов на основе природного полисахарида хитозана. Объектом исследования служили пленочные образцы, полученные из хитозана с молекулярной массой 87000 и степенью дезацетилирования 83,6%, производства ЗАО “Биопрогресс”. Пленки получали методом полива 3%-го раствора полимера в 2%-ой уксусной кислоте на горизонтальную полиэтиленовую подложку при комнатной температуре 48 часов. Характеристики свеже-сформованной пленки: солевая форма хитозана, средняя толщина – 62,7±3,6 мкм, влажность – 17,6%.

Процесс биодеградации полимера проводили в кювете, представляющей собой две плоскопараллельные стеклянные пластинки размером 6×3 см с зазором ≈0,21 мм, скрепленные между собой специальным зажимом. Капиллярный зазор между пластинками устанавливали с помощью калиброванных металлических спейсеров. Диаметр спейсеров измеряли дифракционным методом. Кинетику набухания и растворения пленок изучали на лазерном интерферометре Майкельсона (рис. 3). Образец хитозановой пленки длиной ≈20 мм и шириной ≈0,5 мм помещали вертикально в кювету. Затем кювету с образцом заполняли дистиллированной водой. Кювету устанавливали в одно из плеч интерферометра, настраивая его на горизонтальные полосы конечной ширины. В ходе эксперимента в кювете протекали процессы диффузионного смешения компонентов, в результате которых происходило изменение концентрации полимера и, как следствие, изменение пространственного распределения показателя преломления контролируемой среды. В результате этого во времени изменялась пространственная фазовая модуляция объектной волны AV ( x , t ) в соответствии с уравнением (4), что приводило к изменению формы опорных интерференционных полос.

Эксперименты проводили при температуре 37±1°С. На рис. 6 приведены интерферограммы, наблюдаемые на разных этапах набухания и растворения полимерной пленки в модельной жидкости.

На начальных стадиях процесса наблюдается изображение пленки и прямолинейные горизонтальные опорные полосы в области растворителя (рис. 6, 1 мин). В области изображения пленки наблюдается сложная, нерегулярная картина интерференции -фактически спекл-картина [25], обусловленная оп- тической неоднородностью пленки. В процессе диффузионного смешения пленка становится оптически прозрачной и наблюдается непрерывное изменение показателя преломления по всему сечению кюветы (рис. 6, 6 мин). В результате градиента показателя преломления среды вдоль горизонтальной оси X , происходит изменение кривизны полос. Со временем область искривления полос увеличивается в направлении оси X , что свидетельствует о расширении зоны взаимодиффузии (рис. 6, 16 мин).

Рис.6. Интерферограммы, полученные в процессе массопереноса в системе хитозан – вода

Полученные снимки интерферограмм подвергали компьютерной обработке в графическом редакторе с целью увеличения контрастности и сглаживания спекл-эффекта. Для каждой интерферограммы по точкам пересечения прямой x = const с центрами светлых и темных полос, с учетом коэффициента увеличения β, определяли дискретные значения фазового сдвига AV m ( x j , t k ) , m = 0, ± 1, ± 2,....

По значениям AV _m ( x j , t k ) с использованием формулы (4) рассчитывали дискретные величины изменения показателя преломления среды A n ( x j , t k ) . Путем аппроксимации точек A n ( x j , t k ) функцией Гаусса получали непрерывные зависимости A n ( x , t k ) на разных стадиях процесса диффузии. На рис. 7 приведены зависимости изменения показателя преломления системы в процессе набухания и растворения полимерной пленки в воде. Абсолютная погрешность реконструкции изменения показателя преломления составила 0,0002. Более высокая точность по сравнению с интерферометром Маха-Цендера обусловлена двукратным проходом излучения через кювету.

По кинетике изменения показателя преломления с использованием модели диффузии бесконечно тонкого слоя в неограниченное тело [26] были рассчитаны коэффициенты диффузии D хитозана.

Проведенные эксперименты показали, что метод лазерной интерферометрии с применением увеличительной оптики и специального программного обеспечения может быть успешно применен для моделирования и исследования процессов биодеградации полимеров и оценки их сорбционно-диффузионных параметров.

0,016

0,012

Г 0,008

0,004

0,000

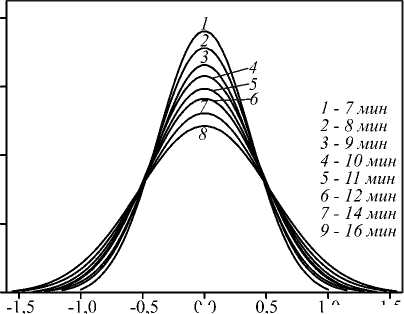
Рис.7. Пространственное распределение изменения показателя преломления системы хитозан – вода в процессе взаимодиффузии

0,0

X, мм

1.0      1,5

Метод муаровых полос для обработки интерферограмм в полосах конечной ширины

В реальном интерферометре поверхности зеркал, делительных пластин, окон кюветы могут иметь отклонения от плоскости и параллельности. Стекло пластин также может быть неоднородным. Все эти погрешности оптических элементов интерферометра приводят к появлению паразитных интерференционных полос в режиме полос бесконечной ширины и к искривлению несущих интерференционных полос в режиме полос конечной ширины. Прямой анализ и обработка таких интерференционных полос усложняется и сопровождается существенными ошибками. Ниже описывается метод обработки интерферограмм в полосах конечной ширины, который позволяет получить так называемые муаровые полосы, совпадающие по форме с интерференционными полосами, которые получились бы в режиме полос бесконечной ширины в интерферометре с идеальными оптическими элементами.

Муаровый метод заключается в вычитании картины несущих интерференционных полос из картины возмущенных объектом полос и в наблюдении образующейся картины муаровых полос. Вычитание картины невозмущенных несущих полос, какой бы они формы не были, приводит к формированию равномерного темного поля в разностном изображении. Возмущенные объектом области с искривленными и смещенными полосами полностью не вычитаются, и в этих областях образуются муаровые полосы. Форма и период муаровых полос качественно и количественно отражают оптические параметры фазового объекта.

Для реализации процедуры вычитания изображений интерференционных картин наиболее эффективным является метод цифровой записи изображений и их численное вычитание с использованием соответствующей программы. Именно такая методика использовалась в настоящей работе. Обратим внимание, что рассматриваемый метод муаровых полос по своей сути полностью совпадает с методом цифровой корреляционной интерферометрии [28,29].

Рассмотрим математические основы муарового метода. Распределение интенсивностей в записываемых интерференционных картинах можно представить в следующем виде:

I 1 ( x , y ) = 2 1 ( x , y ){1 + V cos[ AY 0 ( x , y )]}, (5)

I ₂ ⁽ x , y ) =

= 21(x, y){1 + V cos[AYо (x, y) + AY(x, y)]} ’ где 11 (x, y) и 12 (x, y) - распределения интенсивностей в невозмущенной и возмущенной интерференционных картинах, AY0(x, y) - разность фаз, создающая систему несущих полос конечной ширины, V - коэффициент модуляции (контраст) интерферограммы.

Распределение интенсивности в разностном изображении A I ( x , y ) можно записать в виде:

A I ( x , y ) =

= 4 1 ( x , y )V sin ( AY ₀ + AY/ 2 ) sin ( AY/ 2 ) '

Численное пространственное распределение A I ( x , y ) необходимо преобразовать в изображение – визуализировать. Однако прежде необходимо взять модуль этого выражения, поскольку оно может быть знакопеременным

|^{AI ( x} , y )| =

= 41(x,y)V■ |sin(AYo (x,y) + AY(x,y)/2)|x . (8) x |sin (AY( x, y)/2)|

Если созданная в интерферометре исходная разность фаз AY 0 ( x , y ) существенно более быстро изменяется в пространстве x , y по сравнению с объектной фазовой модуляцией AY ( x , y ) , то период функции |sin ( AY ₀ +AY/ 2)| в уравнении (8) будет существенно меньше периода другой функции |sin ( AY/ 2)|. Пространственное изменение разности фаз AY ₀ ( x , y ) , фактически, определяет несущие (опорные) полосы интерферограммы. Если период несущих полос столь мал, что они практически неразличимы глазом, то это означает, что глаз усредняет эти полосы. Формально, такое усреднение можно ввести в уравнение (8) в виде усреднения по площади S , на которой функция AY ₀ ( x , y ) успевает измениться на 2п радиан, а более медленная функция AY ( x , y ) практически остается неизменной. Тогда для наблюдаемого разностного изображения с усредненным распределением интенсивности получаем выражение

<|A I ( x , y )| >» 2^ I ( x , y )^ V |sin ( ay ( x , y )/ 2)|, (9)

S

Таким образом получили, что разностное изображение интерференционных картин в полосах конечной ширины промодулировано модулем синусоидальной функции. Эта пространственная модуляция и называется картиной муаровых полос. В цифровой корреляционной спекл-интерферометрии [28-30] эти полосы называют полосами корреляции и декорреляции спекл-картин. Период модуля синуса равен π радиан, следовательно, в разностном изображении имеем картину светлых и темных муаровых полос, форма и положение которых определяется уравнениями:

ДТ ( x , y ) = 2 m n

для темных полос,

ДТ ( x , y ) = ( 2 m + 1 ) n                          (11)

для светлых полос.

Уравнение для темных муаровых полос в точности совпадает с уравнением для светлых интерференционных полос для того же фазового возмущения ДТ( x, y), наблюдаемых в режиме полос бесконечной ширины. Это необходимо учитывать при обработке муаровых полос в разностном изображе- нии.

На рис.8 показаны смоделированные интерференционные картины в полосах конечной ширины – невозмущенные и возмущенные объектом, а также показано разностное изображение с системой муаровых полос. Вышеописанный процесс усреднения интерференционных полос можно пронаблюдать, рассматривая разностные картины с различного расстояния.

Рис.8. Смоделированные интерференционные картины в полосах конечной ширины (а, б) и разностное изображение (в) с муаровыми полосами: а – несущие интерференционные полосы; б – полосы, возмущенные фазовым объектом

Для эффективной реализации муарового метода необходимо иметь несущие полосы как можно меньшего периода Л . Однако при этом система полос должна разрешаться используемой ПЗС-матрицей и должна четко проявляться в цифровых изображениях.

Метод муаровых полос мы использовали, в частности, для исследования процессов биодеградации полимера. На рис. 9 приведены фотографии интерферограмм в полосах конечной ширины на различных стадиях процесса растворения пленки хитозана в дистиллированной воде и соответствующие разно- стные изображения с муаровыми полосами, отчет- ливо характеризующими процесс изменения показателя преломления в изучаемой среде.

Рис.9. Реализация метода муаровых полос: интерференционные полосы конечной ширины невозмущенной (а) и возмущенной интерферограмм (б, г, ,д) и результаты их попарного численного вычитания (в, е)

Лазерная многолучевая интерференционная микроскопия

В случаях, когда необходимо высокое пространственное разрешение для наблюдения пространственной структуры фазового объекта, применяется метод интерференционной микроскопии [1,3-5]. В основе этого метода лежит явление многолучевой интерференции света в капилляре клинообразной кюветы с высокоотражающими внутренними поверхностями. При прохождении пучка монохроматического света через такую кювету вследствие разности хода прошедшего и отраженного лучей в области клина возникает многолучевая интерференционная картина в виде системы параллельных светлых и темных полос.

Кинетику взаимодиффузии в системе глицерин – вода исследовали на лазерном многолучевом микроинтерферометре на основе микроскопа с цифровой записью изображения [3,5]. Необходимость использования микроскопа с достаточно большим увеличением, а значит и высоким пространственным разрешением, обусловлена большим градиентом показателя преломления и, следовательно, высокой пространственной частотой интерференционных полос, возникающих в области контакта глицерина с водой. Схема экспериментальной установки приведена на рис. 10.

Кювету с исследуемой системой помещали на предметный столик микроскопа. Объектив микроскопа MO формировал увеличенное изображение зазора кюветы на ПЗС матрице (DMC-300). В экспериментах велась непрерывная запись кадров цифровых интерферограмм на жесткий диск компьютера. Вращающееся матовое стекло в освещающем пучке использовали для подавления спекл-модуляции в изображении. В экспериментах использовали клинообразные кюветы, составленные из стеклянных пластин, внутренние стороны которых покрыты слоем металла с достаточно высоким коэффициентом отражения R « 0,6 - 0,7 . Воздушный клин между пластинами устанавливали с помощью калиб- рованного металлического спейсера толщиной 100 мкм, угол клина составлял а» 0,5° . Источником света служил He-Ne лазер.

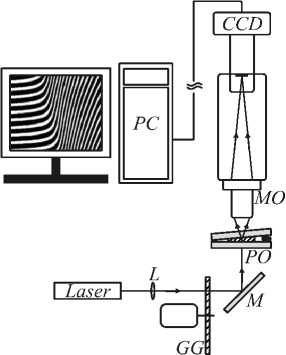
Рис. 10. Схема многолучевого микроинтерферометра: L – расширитель пучка; PO – кювета с изучаемым фазовым объектом; M – поворотное зеркало; MO – микрообъектив; GG – вращающееся матовое стекло;

CCD – ПЗС-камера; PC – компьютер

Методика эксперимента на многолучевом микроинтерферометре состояла в следующем. На металлизированную поверхность одной из стеклянных пластин наносили небольшой объем глицерина, затем устанавливали калиброванный спейсер, накрывали второй пластиной и закрепляли специальным фиксатором. Кювету помещали на предметный столик микроскопа и настраивали изображение на границу раздела глицерин-воздух перпендикулярно интерференционным полосам (рис. 11, a). Затем клинообразный воздушный зазор кюветы заполняли дистиллированной водой. По изменению интерференционной картины наблюдали процесс взаимо-смешения жидкостей. Изменяющуюся картину интерференционных полос фиксировали ПЗС – камерой через определенные интервалы времени. На рис. 11 приведены интерферограммы, наблюдаемые в процессе массопереноса в системе глицерин – вода.

Горизонтальные, практически параллельные друг другу и без взаимных искажений опорные интерференционные полосы в областях глицерина и воздуха свидетельствуют о постоянном показателе преломления этих сред (рис. 11а). При введении в кювету воды в области соприкосновения жидкостей имеет место резкий скачок показателя преломления и, соответственно, наблюдается резкий изгиб интерференционных полос (рис. 11б). Анализ картины показывает, что в области взаимодиффузии имеет место непрерывное изменение показателя преломления (рис. 11б-з), что свидетельствует о формировании молекулярных растворов компонентов смеси. C течением времени наблюдается расширение области искривления интерференционных полос, что свидетельствует о расширении зоны взаимодиффузии (рис.5б-з). Поэтому по интерференционным картинам возможно определение кон- центрационного профиля системы глицерин – вода в процессе массопереноса.

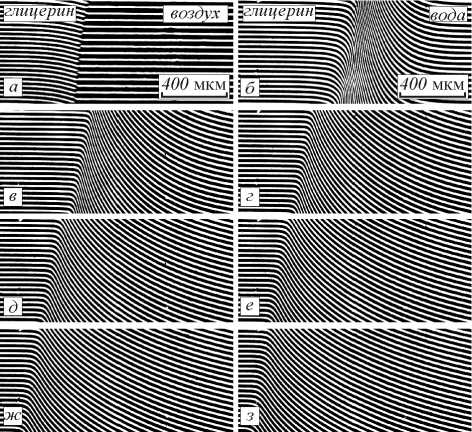
Рис. 11. Интерференционные картины, полученные в процессе массопереноса в системе глицерин – вода: (а) t=0 мин, (б) t=8 сек, (в) t=1 мин 50 сек, (г) t=3 мин 32 сек, (д) t=5 мин 14 сек, (е) t=6 мин 56 сек, (ж) t=8 мин 38 сек, (з) t=10 мин 20 сек

Количественная обработка многолучевых интерферограмм основывалась на следующем теоретическом анализе. В отличие от интерферометров Маха-Цендера и Майкельсона, где наблюдается двулучевая интерференция, в данном методе формирования интерференционной картины участвует множество лучей, испытавших различное число отражений внутри кюветы, как это происходит в интерферометре Фабри-Перо, в котором интерференционная картина наблюдается в бесконечности – в задней фокальной плоскости линзы [18,19]. В рассматриваемом методе локализованная интерференционная картина наблюдается в изображении клина, где также имеет место многолучевая интерференция света, что обуславливается, как мы полагаем, конечной разрешающей способностью микроскопа, собирающего лучи света в каждую точку изображения от достаточно протяженной области клина, определяемой областью разрешения микроскопа. При многолучевой интерференции для распределения интенсивности в интерференционной картине приближенно можно использовать формулу Эйри [18,19], полученную для конечного числа отражений 2 N в клине в пределах области разрешения микроскопа, без учета поглощения и возможных фазовых сдвигов при отражении от металлических поверхностей клина

I ( x , У ) = I о ( 1 - R 2 ) ^х

[ 1 + R ² N - 2 R N cos N ДТ ( x , у ) ] ,             ⁽¹²⁾

между лучами света 3-х и 1-но кратно, 5-ти и 3-х кратно и т.д., прошедшими через клинообразную кювету

2п             2п

АТ ( x , у ) ® —2 d ( У ) n ( x )-“ 2 а уп ( x ) ,     (13)

где d (у) ® а у - локальная толщина клина, линейно изменяющаяся в направлении оси Y , перпендикулярной ребру клина, а - угол клина, п (x) - ло- кальное значение показателя преломления среды внутри кюветы, которое изменяется в направлении оси X (вдоль ребра клина) при переходе от одной полосы к другой (рис. 12а).

В пространственном распределении интенсивности I (x, у), определяемой уравнением (12), при достаточно большом коэффициенте отражения R ® 0,7 - 0,8 и не очень большом числе интерферирующих лучей N имеют место относительно острые локальные максимумы – светлые интерференционные полосы при АТ (x, у) = 2п m и более широкие минимумы - тем ные полосы при АТ (x, у) = (2m + 1)п (см. интерферограммы на рис.11).

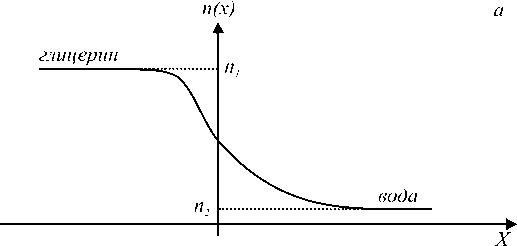
Рис. 12. Пространственное изменение показателя преломления в области взаимодиффузии в системе глицерин – вода (a) и соответствующая картина интерференционных полос, наблюдаемая в клинообразной кювете с жидкостями (б)

Пространственный период интерференционных полос вдоль оси Y определяется выражением

X

Л у (x )* э—rV 2а п (x)

В области глицерина он равен Л _у 1 ® X/2 а п 1 , а в области воды - Л _{у 2} ® X/2 а п ₂ . В области взаимодиф-фузии период Л _у изменяется от значения Л 1 до Л ₂.

Пространственный период полос вдоль оси X обратно пропорционален пространственной скорости изменения показателя преломления Ап (x )/Ax и определяется выражением

А п ( x ) A x

X Г

Л (x, у) ® x        2ау (

В области чистого глицерина и чистой воды п = const и период полос Л _x = да при горизонтальных опорных полосах.

Уравнение (13) позволяет определить профиль показателя преломления п ( x ) по наблюдаемой интерференционной картине при известных значениях п 1 и п ₂. Согласно (13) разность фаз АТ ( x , у ) вдоль оси X изменяется от значения АТ 1 = 4 па уп 1 /X в области глицерина до значения АТ ₂ ® 4 па уп ₂ /X в области воды. Если это изменение равно 2 п M , где M - целое, то прямая у = сопз1 (рис. 12б) пересекает M светлых или темных интерференционных полос, количество которых определяется разностью показателей преломления п 1 - п ₂. Следуя работе [5], можно ввести относительную величину – инкремент показателя преломления

п - п2    X

N ( у ) =Лт^ ^^,                (16)

M   2ау зависящую от а и у , которая позволяет определять по интерференционной картине кривую изменения показателя преломления п (x). Действительно, разность фаз АТ (x) можно представить в виде АТ (x) = АТ1 - 2пm (x), где m (x) - число интерференционных полос, пересекаемых прямой у = const в направлении от области с чистым глицерином до точки с определенной координатой X . Тогда для п (x) из уравнения (13) получим выражение п (x)® п1 - m (x) N (у), (17) где число m (x) может быть и дробным, если отсчет пересечений прямой и интерференционных полос ведется с точностью до долей их периода Лx.

Методика обработки интерферограмм заключалась в следующем. Для линии равной толщине клина кюветы у = сапз1, перпендикулярной границе раздела жидкостей в кювете (рис. 11), определялся инкремент показателя преломления N (у) с использованием (16). Значения n1 и n2 определяли на рефрактометре ИРФ-22. В наших экспериментах эти значения оказались равными п1 = 1,4729, п2 = 1,3300 . Для каждой интерферограммы, зарегистрированной в определенный момент времени tk , в процессе взаимодиффузии глицерина и воды опре- деляли m (x) - число пересечений прямой y = const темных и светлых интерференционных полос между областью чистого глицерина до данной точки интерферограммы. Фактически, определяли координаты центров светлых и темных интерференционных полос xj и соответствующие им числа m (xj). С использованием уравнения (17) определяли дискретные значения профиля показателя преломления n (xj) = n - m (xj, tk) N (y) для каждого выбранного момента времени tk процесса взаимодиффузии.

На рис.13 представлены рассчитанные по интерференционным картинам профили пространственного распределения показателя преломления n ( x ) в различные моменты времени в процессе самопроизвольного смешения компонентов системы глицерин–вода. Абсолютная погрешность реконструкции показателя преломления составила по нашим оценкам 0,0001.

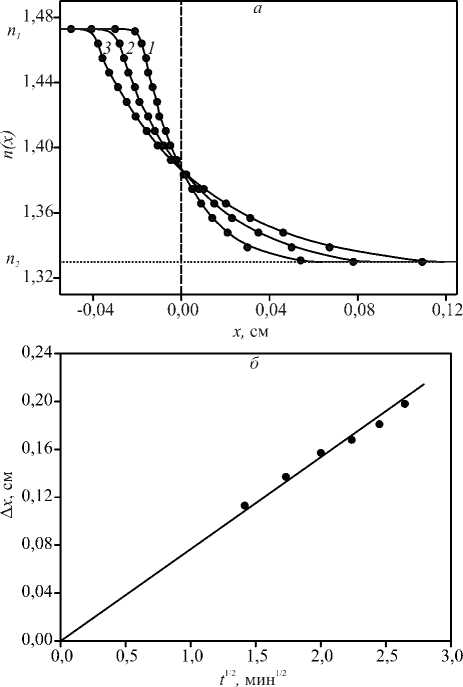
Рис.13. а) Пространственное распределение показателя преломления в системе глицерин – вода в различные моменты времени процесса взаимодиффузии: 40 сек (1), 2 мин (2) и 4 мин (3). б) Временная зависимость размера диффузионной зоны

Из рис. 13а видно, что в зоне взаимодиффузии компонентов наблюдается формирование концентрационного профиля с непрерывным изменением состава от одного компонента к другому. С течением времени размеры профиля пространственно- го распределения показателя преломления n (x) и, соответственно, концентрации c (x) увеличиваются, а перемещение координат xi (ci) изокон-центрационных плоскостей (сечений) относительно любой системы отсчета подчиняется диффузионной закономерности Ax ~ t1/2 (рис. 13б).

Поскольку в данной системе показатель преломления линейно зависит от концентрации, то он фактически определяет концентрационный профиль вещества в изучаемой среде. Данные по концентрационному профилю c ( x ) и его изменению во времени позволяют получить концентрационную зависимость коэффициентов взаи-модиффузии. Коэффициенты массопереноса компонентов в системе глицерин–вода рассчитывали по теории Матано–Больцмана [5], согласно которой рассматривается второй закон Фика для одномерной диффузии вещества (18) при следующих начальных (19) и граничных (20) условиях:

5c = д Г d 5 c ।д t 5x ( 5x J ’

t = 0: с = 1 при x <  0 и с = 0 при x >  0,    (19)

dc

— = 0 при x = +ж .                      (20)

dx

На рис. 14 представлена полученная концентрационная зависимость коэффициентов взаимо-диффузии. Погрешность определения коэффициентов диффузии составила, по нашим оценкам, не более 8%.

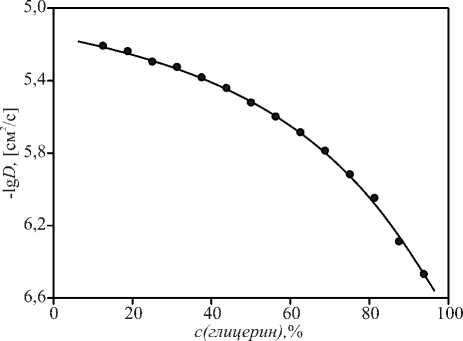
Рис. 14. Концентрационная зависимость коэффициента диффузии глицерина, рассчитанная по профилям пространственного распределения концентрации в процессе самопроизвольного смешения компонентов в системе глицерин–вода

Как видно из рис. 14, зависимость - lg D = f (c) описывается плавной выпуклой кривой. С увеличениием концентрации глицерина в смеси (например, с 10% до 90%) величина коэффициента диффузии этого компонента в водной среде уменьшается более, чем на порядок.

Известно, что глицерин широко используется в технологии синтеза органических веществ и производства пластических масс, в лакокрасочной, текстильной, пищевой и косметической промышленности, в сельском хозяйстве и др. Хорошая смешиваемость с водой (высокая гигроскопичность) открывает широкие возможности применения глицерина в медицине и фармакологии, в частности, в качестве лекарственных средств, наполнителя и растворителя фармацевтических препаратов, смягчителя тканей, компонента формовочных растворов для капсулирования биологически активных веществ. Значительное снижение температуры кристаллизации смесей глицерин–вода в сравнении с безводным глицерином предопределяет перспективность их использования для замораживания эритроцитов, роговицы глаза и других живых тканей.

Заключение

Как показали эксперименты, методы лазерной интерферометрии могут эффективно использоваться для изучения процессов взаимодиффузии (смешения и растворения) компонентов бинарных систем, определения профилей распределения показателей преломления и концентрации, расчета коэффициентов взаимодиффузии в широкой области составов.

Лазерные интерферометры Маха-Цендера и Майкельсона могут достаточно эффективно использоваться для исследования кинетики процессов взаимодиффузии в системе полимер-растворитель. Применение достаточно простых оптических компонентов, средств настройки интерферометра и защиты от внешних вибраций позволяет получать стабильные и высококонтрастные интерференционные картины, отражающие пространственные распределения показателя преломления тонкого фазового объекта. Использование цифровой фоторегистрации с последующей численной обработкой изображений позволяет с достаточно высокой точностью контролировать кинетику процесса диффузии полимера. Погрешность определения коэффициентов диффузии в этих измерениях составляет менее 10% при точности измерения изменения показателя преломления ≈ 0,0003.

Для достижения более высокого пространственного разрешения интерференционной картины при больших градиентах показателя преломления требуется применение высококачественных объективов с достаточно малым фокусным расстоянием и высокой числовой апертурой. Спекл-модуляция интерференционных картин в лазерном свете частично ограничивает точность измерений и разрешающую способность.

В этих условиях предпочтительнее применение метода многолучевой интерференционной лазерной микроскопии с использованием специальной клиновидной кюветы, вращающегося матового стекла для подавления спекл-модуляции и микроскопа с циф- ровой регистрацией кадров изображений. Использование данной системы позволяет получать высокое пространственное разрешение интерференционной картины при одновременном сглаживании спекл– модуляции подвижным рассеивателем и снижении влияния внешних вибраций на наблюдаемую картину интерференционных полос. Точность реконструкции показателя преломления составляет ≈0,0001, что обеспечивает возможность определения коэффициентов диффузии с погрешностью 5-8% в зависимости от концентрационной области. К преимуществам многолучевого микроинтерферометра следует также отнести компактность установки, к недостаткам – необходимость изготовления стекол с металлическим напылением, разрушающимся в процессе экспериментов.

Исследование кинетики и динамики массоперено-са веществ в бинарных средах методами лазерной интерферометрии позволяет, с одной стороны, использовать результаты интерференционных измерений для изучения диффузионных характеристик систем механизма набухания и растворения компонентов, с другой - решать целый ряд практических задач. Например, прогнозировать диффузионную подвижность компонентов, оценивать молекулярные, фазовые, термодинамические и другие характеристики систем и материалов на их основе, что имеет важное практическое значение для целого ряда современных промышленных и медицинских технологий.

Работа выполнена при частичной поддержке гранта Президента для поддержки ведущих научных школ РФ НШ-208-2008.2 и гранта аналитической ведомственной целевой программы “Развитие научного потенциала высшей школы (2006-2008)”, код проекта РНП 2.1.1.4473.