Исследование продольного краевого эффекта в двухсторонних линейных индукционных машинах с жидкометаллическим ротором

В настоящее время перспективным направлением в области энергетики является атомная промышленность. С ростом мощностей атомных электростанций растут требования к оборудованию, осуществляющему технологические процессы. Основой оборудования служат системы перекачивания жидкого теплоносителя. В них используются магнитогидродинамические (МГД) насосы индукционного и кондукционного типов, в зависимости от условий эксплуатации. Использование кондукционных насосов не всегда представляется возможным из-за многих факторов, один из которых перекачивание агрессивных высокотемпературных сред. Следовательно, приходится прибегать к линейным индукционным МГД-насосам, основным недостатком которых считают продольный и поперечный краевые эффекты.

Конечная длина индукторов линейных индукционных машин (ЛИМ) обуславливает появление в возбуждающем поле кроме бегущей волны две стоячие пульсирующие волны. При наличии в зазоре вторичного проводящего и движущегося тела в последнем возникают не только ответные бегущие волны тока и поля, но и дополнительные токи и поля, оказывающие, как правило, тормозное действие, увеличивающие потери и снижающие к. п. д. машины в целом. В некоторых случаях вредное влияние продольного краевого эффекта может быть очень значительным.

Проблеме изучения продольного краевого эффекта посвящено большое количество работ, одна из них [1]. Обычно на современном этапе делаются попытки решения двух- и трехмерных задач, что неизбежно приводит к численному анализу и чрезвычайно затрудняет понимание физики явления и его особенностей. Поэтому представляется целесообразным рассматривать одномерную модель с такими упрощениями, которые минимально искажают реальную физическую картину явления и в то же время позволяют максимально упростить математическое решение задачи. С этой целью мы воспользуемся расчетной моделью, предложенной и проанализированной А. И. Вольдеком [2, 3].

Расчетная модель и принятые допущения

Эскиз плоской линейной индукционной машины (ПЛИН) представлен на рис. 1 и включает в себя: 1 – магнитопроводы; 2 – многофазные обмотки; 3 – стенку канала толщиной χ; 4 – жидкий металл, движущийся со скоростью υ. Индукторы расположены на расстоянии δ от центра канала с жидким металлом и имеют длину L = 2 p т, где p - число пар полюсов; т - полюсное деление.

Для анализа электромагнитных характеристик были приняты следующие основные допущения:

• 1.    Магнитопроводы индукторов имеют магнитную проницаемость ц = да и электропровод -ность γ = 0.

• 2.    Поперечный краевой эффект отсутствует, т.е. ширина индукторов по оси у не ограничена.

• 3.    Система имеет бесконечную длину в направлении оси у, т.е. электромагнитное поле явля-

• ется плоскопараллельным. Вектор комплексной напряженности электрического поля E = eyEy, – 241 –

• 4.    Систему координат принимаем жестко связанной с индукторами, при этом все элементы жидкого металла в канале двигаются относительно индукторов с одинаковой скоростью υ.

• 5.    Влияние пазов учитывается обмотками, представленными бесконечно тонкими токовыми слоями, расположенными на поверхности индуктора с комплексной линейной плотностью тока:

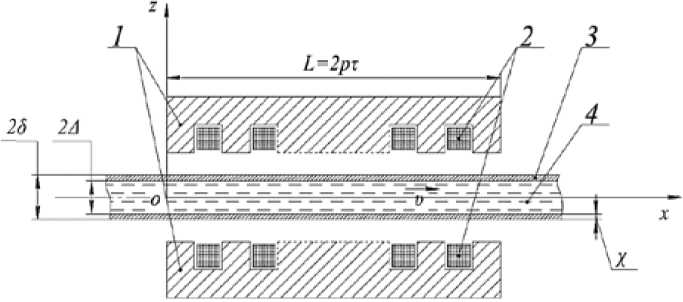
Рис. 1. Эскиз плоской линейной индукционной машины

Fig. 1. Sketch of a flat linear induction machine

J & m = Je^{i ϕ} m ,                                                                              (1)

где J – линейная плотность тока; i =- 1 – мнимая единица; φ m – начальный угол фазы m.

При принятых допущениях расчетная модель будет иметь вид, изображенный на рис. 2.

Математическая модель линейной индукционной машины

Решение будем проводить в двух областях: 1 – 0 ≤ z < Δ; 2 – Δ <  z ≤ δ. Для напряженности электрического поля справедливы дифференциальные уравнения.

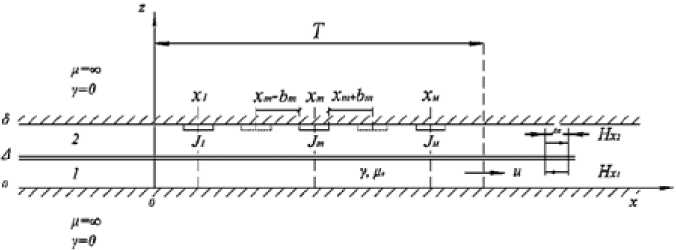
Рис. 2. Расчетная модель МГД-насоса

Fig. 2. MHD-pump design model

Для области 1, 0 ≤ z < Δ:

∂ ² E ₁ ∂ ² E ₁ ∂ z ^{2 +} ∂ x ²

-

∂ ² E i M o Y® E i ^- М о Г и -Г"¹ = ⁰ , ∂ x

где ц0 = 4п10^-7 [ Гн/м] - магнитная постоянная; у [Ом/м] - удельное сопротивление; ю = 2п f [ рад/с ] – угловая частота; u [ м/с ] – скорость движения жидкого металла.

Для области 2, Δ <  z ≤ δ:

E +

5z

Граничные условия:

d ² E, „ ---22 = 0 .

5x

5 2 А     о IT" .о -0; (4) д2Е&2      J-i®Ho^Jm ; Xm - bm < X < Xm + bm дz z=,-I               0                ; (5) дE  дE. 2- _ дz    дz          % г z_д ’ (6) где σ [См] – удельная проводимость; χ [м] – толщина стенки канала.

Решение дифференциальных уравнений

Полагая, что электромагнитное поле периодично по координате x с периодом T, будем искать решения в виде рядов Фурье в комплексной форме [4]:

EV 2 = Z ^EV 2n e ik n ^;

T

E 2. = - J E 2 e - k ^XдX .

T ₀

Умножив уравнения (2) и (3) на функцию e ние по x от 0 до T , получим:

ik x n и проинтегрировав получившееся выраже-

d ² E ^&

тт - % = о;

dz d2E

---2— k1 E = 0;

z           2nπ где ϕn=kn2+iµ0γω+iknµ0γuτ; kn =

^τ

Общими решениями обыкновенных дифференциальных уравнений (9) и (10) являются:

Ei n = Ai e" + A2 e;";

E2n = A3ekn + A4e-knz .

n

Постоянные интегрирования A i ^ A ₄ определяются из граничных условий (4-6).

Подставив полученные постоянные интегрирования из граничных условий в (11) и (12),

E1 n(z)       /1     ’

Q n

E n (z) = -      , nQn где Qn=knchϕnΔshkn(δ-Δ)+Gnchkn(δ-Δ);

θ n ( z ) = k n ch ϕ n Δ ch k n ( z - Δ ) + G n s hk n ( z - Δ ) ;

G n = ϕ n sh ϕ n Δ + ξ ch ϕ n Δ ;

• ξ = i ε k χπ ²;

ωµ 0 σ k 2

• ^e k = n^{2 T .}

Преобразовав (13) и (14), имеем:

n =+∞ _Ψ

n ( x ,')=T^r ^e n (z) e k ;

n =-∞ k n Q n

M    xm+bm где *n - -^ X -Jm I e m=1    xm-bm

-

i_kx.     .2 ®^) A •

∂x=-i     ∑ Jmsin(knbm)e knT m=1

- ik n x m

-

2 ωµ ₀

^{i       C}n 1 ;

k T ^{n 1}

C n 1 :L ' sin( k n b m )e - k n x m .

m = 1

Окончательно получим

2 ωµ ^{n = + ∞} ch ϕ z     ikx

E _{1 n} ( x , z ) =- i     ⁰ ∑ ⁿ C_{n 1} e ^iknx ;

T n =-∞ k n Q n

^& (   ) - ² ω^{µ 0 n =+∞ Cn 1} () ^iknx

2 n x ,               ∑ 2 n e

T   n =-∞ k n Q n

.

По известным уравнениям электромагнитного поля определим составляющие вектора магнитной индукции. Из rotE = - i to B :

B & x = ^{1 ∂ E y} ; i ω ∂ z

∂ E

B z = ^{1 y} i ω ∂ x

.

Преобразовав (19) и (20) в соответствии с (17) и (18), получим:

^Bx 1 ⁼

_- 2 µ 0 ^{n =+∞} ϕ n sh ϕ n z _Ce ik_nx T n ^∑ =-∞ k n Q n   ^{n 1}

B

sh ϕ _n z Q n

ik n x

^Cn 1 e

n =+∞

^T n =-∞ ^kn Q n

B & z 2 =- ^{i 2 µ} 0 ∑ ^Cn 1 θ ' n ( z ) e ^ik n ^x ,

T   n = - ∞ k n Q n

где θ ' _n ( z ) = P _n shk _n ( z - Δ ) + G _n chk _n ( z - Δ ) .

Интегральные и дифференциальные характеристики линейной индукционной машины

Комплексная электромагнитная мощность, отдаваемая обмоткой индуктора в зазор, равна:

M x m + b x            _*

M*                i где Cn2 = ∑ J msin(knbm)ei m=1

m = 1

^m   x_m - b_x

m

i 8 ωµ 0 l _∑ C n ₃1 C n 2 _{θ n ( δ ) ,} T n =-∞ k n Q n

Электромагнитная сила, действующая на индуктор:

r

F em

M X m + b m            *

= Re 21^ J Bz 2( x ,5) Jm a m=1^

L         ^x m b m

= Re J i 8^ £ CC- [ ^ ( 5 ) L

2 ⁿ

I ^T n=- k „ Q „

Приведем мощность к безразмерному виду. Для начала домножим и разделим все величины, входящие в A на т, отсюда

Q n

,   2 n n _ 2 n n

kv = _ = = A

T

A T где ^T =-• ^т

Л

T

,

A

Фп =

2 пп

2n

+ tern2 + i — en2 (1 - s),

T

^Y® гдеe="tr-

2 т .

Преобразуем (25) в соответствии с полученными значениями:

S em = i ^S ' lT- п

J 2 n f ^ . ( ^ ) _C * _C *

^J b Z^ 3 C . 1 C . 2 , . =- . Q .

□

A    M A где C. 1 =ZJm sin(k,b. )e"*■"■ m=1

; Cn 2 =Z Jm *Sin( knbm ) e m=1

A ik n x m ; J _m

J m ; J, J _b

A

*

m

*

J _m          w _m I _m

^; J b ^

J b       m = 1 ² P^T

.

Поделим Sem на базисную мощность, чтобы привести ее к безразмерному виду. За базис- ную мощность примем

ωµ 0 lT S =

π

² _Jb 2 _.

Окончательно

_∧               n =+∞

S ^∧ em = i ^{S em} = i ∑

S

θ n ( δ )

n =-∞

n ³ Q n

∧ ∧