Исследование проекций лучевых и каустических структур в координатно-импульсных подпространствах предканонического оператора Маслова

ВЕСТНИК 2015

геометрической оптики, КОМ позволяет получить равномерные асимптотические решения волновых уравнений не только в регулярных, но и в сингулярных областях, которым соответствуют каустики (огибающие лучевых семейств) и их особенности [5–8]. Как известно, на каустиках расходимость лучевого потока, описываемая якобианом расходимости, обращается в нуль, что и приводит к бесконечностям для лучевых решений. Основная идея метода КОМ [5; 6; 9; 10] состоит в том, что в силу теоремы Коши для обыкновенных дифференциальных уравнений при выполнении необходимых условий относитель-

ВЕСТНИК 2015

но гладкости правых частей решения бихарак-теристической системы Гамильтона в фазовом пространстве однозначно параметризуются и не пересекаются. Каустики возникают лишь при проектировании фазового пространства в конфигурационное. Если же выбрать другое подпространство фазового пространства (импульсное или смешанное), то в нем лучевые траектории могут не пересекаться, а якобиан расходимости не будет обращаться в нуль. Конечно, такое лучевое представление не будет являться решением исходной задачи, но, как показано в работах [5; 9–11], его фурье-образ является искомым решением. В результате получается быстро-осциллирующий интеграл (предканонический оператор), кратность которого определяется числом компонент импульса (волновых векторов), участвующих в формировании координатноимпульсного подпространства.

В общем случае можно показать (см., например, [12]), что всегда существует такая проекция фазового пространства в координатноимпульсное подпространство, в котором отсутствуют каустики и их особенности. Но это утверждение справедливо только локально. Поэтому для построения глобального решения задачи необходимо сшивать различные «карты», переходя от одного координатно-импульсного представления к другому.

Необходимо отметить, что лучевая структура и каустические особенности, возникающие в импульсных или смешанных подпространствах в случае ионосферного распространения радиоволн, изучены недостаточно подробно, в отличие от аналогичных результатов [13–18], полученных для конфигурационного (координатного) пространства. Чтобы восполнить этот пробел, в настоящей работе выполнено исследование лучевых и каустических структур в координатноимпульсных подпространствах предканони-ческого оператора Маслова. Рассмотрены две ситуации: распространение в возмущенном и невозмущенном ионосферном слое и изучены особенности, возникающие в координатноимпульсных пространствах при возмущении ионосферной плазмы.

2. Модель эффективной диэлектрической проницаемости ионосферы Земли

В настоящей работе рассмотрена изотропная модель эффективной диэлектрической проницаемости ионосферной плазмы, то есть модель, не учитывающая магнитного поля Земли:

v =

_4ne ² N

=           , me®®

где e = 4,8029 10 ^-10 СГСЭ - заряд электрона, m e = 9,108 10 ²⁸ г - масса электрона, N - величина электронной концентрации в фиксированной точке пространства, а ω – круговая частота излучения.

Модель электронной концентрации ионосферы представим в виде

^{n (} r ) - N ₀ Ui ¹ - ⁹ -

exp ( -9 ) cos X

+

в

⁺ yexp

z - z02 / 2 | zm 2    )

p

,

z - z 01

zm1 2 , где

N s = в sin

n x

z ^- z 02

V z m 2

относительная частота спорадического слоя, а

^Np = ^в р exP

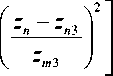
x n - x n 3 | У - У 03 |

II

xy m 3             y m 3

-

относительная частота возмущения.

В формулах (3–4) введены параметры: z ₀₁ – высота максимума слоя F2 , z_{m 1} – условная полутолщина слоя F2 , β – безразмерный коэффициент, характеризующий степень ионизации спорадического слоя и слоя E по отношению к основному, z ₀₂ – высота максимума спорадического слоя, z ₀₂/2 – высота максимума нижнего слоя E , z_{m 2} – условная полутолщина нижних слоев, величина N ₀ – электронная концентрация в максимуме основного слоя F2. При вычислении применялись следующие значения этих параметров: N₀ = 2 10 6 см 3 , z m ₁ = 100 км, z ₀₁ = 300 км, z m 2 = 10 км, z ₀₂ = 200 км, x = 0. Характерный горизонтальный размер спорадического слоя x_s = 600 км.

В формуле (5), описывающей эллиптическое возмущение, x_{m 3}= 15 км, y_{m 3}= 10 км, z_{m 3}= 10 км, причем эллипсоид повернут:

Г x_n = x cos( 9 _t) - z sin( 9 _;t)

[ zn = x sin(9;t) + z cos(9x) , xn3 = x3c0S№ ) - z3sin(9A ) .zn3 = x3sin(9A ) + z3cos№ )

В выражениях (6) x ₃ = 75 км, z ₃ = 290 км, а угол поворота θ_λ равен 10°. Параметр β_p – это безразмерный коэффициент, характеризующий степень ионизации возмущения.

Ниже сопоставлены два случая: β = 0, β = 0 и в = 0,3, e p = - 0,3 •                           p

Электронная концентрация

3. Расширенная бихарактеристическая система уравнений

Для вычисления лучевых траекторий в фазовом пространстве координат и волновых векторов в работе применена бихарактеристическая система уравнений [5; 19]:

—

dr _ дГ /дГ dk _ дГ /дГ dt     д k д to , dt д r д го ’

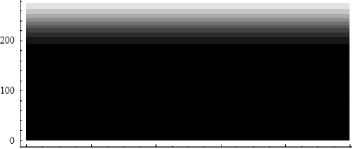
О            200           400           600           800          1000

Рис. 1.

с гамильтонианом:

Г= k x + k y ² + k z - -г ^ ( Г, го ),              (8)

где r _ ( x , y , z ) - координаты точки наблюдения, к _ ( k_x , k y , k z ) - волновой вектор, го _ 2 п *13,25 10 6 с ^-1 - круговая частота излучения, t - групповое время, ^ ( ^- , го ) - эффективная диэлектрическая проницаемость среды распространения, с _ 2,99 7925 10 ⁸ м/с - скорость света.

Систему (7–8) необходимо дополнить начальными условиями. Пр е дположим, что начальный волновой вектор k (0) параметрически зависит от углов выхода луча:

k _x (0) _ to V ^ 0 cos z cos , - ^k - ^{(0) _} "^ Vs™ ^{z cos n} . c

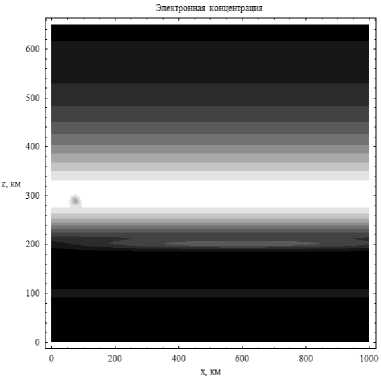
Рис. 2

Электронная концентрация ионосферы, в = 0, e p = 0 - рис. 1 и в = 0,3, Р_р = - 0,3 — рис. 2

го kz (0) _— Vf0 sinn, c

величина ε ₀ – это значение эффективной диэлектрической проницаемости среды в источнике, а точечный источник излучения находится вне ионосферной плазмы и расположен в начале координат ( x 0 _ y 0 _ z 0 _ 0):

^-l t _ 0 ^_ ( ^x 0 , У 0 , z 0 ) .                                 ⁽¹⁰⁾

Однако для вычисления расходимости лучевых потоков необходимо перейти к расширенной бихарактеристической системе [15; 20; 21], дополнив (7-8) уравнениями:, d^z _ д \ дГ /dr) dkz _ d ГдГ /dF^ dt” dZ (d 1^1 droJ, dT ~ dZ (dF/ dro ) '

ВЕСТНИК 2015

d F _	d	Г dF	/ dF^	dk n	_ d	' dF	/ dF
dt	dn	(d £/	d ro ;	’     dT	d n l	. d Г /	d ro

На рис. 1 и 2 показаны линии равного уровня электронной концентрации ионосферной плазмы в невозмущенном (рис. 1) и в возмущенном случаях. На рис. 2 помимо слоя F2, представленного также и на рис. 1, мы видим слой E на высоте 100 км, спорадический слой на высоте 200 км и локальное возмущение (понижение электронной концентрации) эллиптической формы на высоте 290 км.

с соответствующими начальными условиями:

k_x ′ _ξ (0) =- ^ω ε ₀ sin ζ cos η , k_x ′ (0) =- ^ω ε ₀ cos ζ sin η , c                     η c

k_y ′ _ξ (0) =- ^ω ε ₀ sin ζ sin η , k ′ _{y η} (0) = ^ω ε ₀ cos ζ cos η ,

k z ′ ξ (0) = ^ω _c ε 0 cos ζ , k z ′ η (0) = 0 ,

r ζ ′ (0) = 0 , r η ′ (0) = 0 . (12)

Предположим, что распространение электромагнитной волны изначально осуществляется в плоскости ( x , z ), то есть ζ = 0.

• 4.    Лучевое распространение в фазовом пространстве

Рассмотрим структуру лучевых траекторий в различных двумерных проекциях фазового пространства, сопоставляя невозмущенный (нечетные номера рисунков) и возмущенный (четные номера рисунков) случаи.

На рис. 3 показана лучевая структура радиосигнала в случае распространения волны в плоскости ( x , z ) в невозмущенном случае, а на рис. 4 такая же структура показана для возмущенного случая. Рис. 3 типичен для однослоевой модели. С ростом угла выхода луча ( η ) лучи, отражаясь от ионосферного слоя F, образуют верхнюю каустику, затем точку возврата (каустическое острие), нижнюю каустику и, наконец, начинают просачиваться через ионосферный слой.

ВЕСТНИК 2015

Рис. 3.

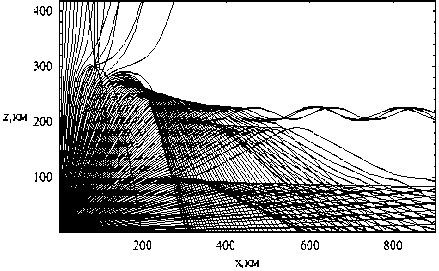
Рис. 4.

Лучевая структура в плоскости ( x , z ); невозмущенный случай – рис. 3; возмущенный случай – рис. 4

На рис. 4 лучевая структура существенно сложнее. С ростом угла выхода лучи сначала образуют каустическое острие, связанное с нижним слоем E (см. рис. 2), затем возникает острие, вызванное спорадическим слоем, и только по- том образуется каустическое острие слоя F, причем между двумя последними топологическими структурами возникает волновой канал, в котором на рис. 4 находятся несколько лучей. Что касается локальной неоднородности, о которой шла речь выше, то ей соответствует фокусировка лучей выше и левее каустического острия слоя F.

В отсутствие магнитного поля и поперечных горизонтальных градиентов луч не выходит из плоскости первоначального распространения. Поэтому проекции лучевых траекторий в плоскостях ( y, z ) и ( x, y ) ниже не приводятся.

Перейдем теперь к смешанным координатноимпульсным подпространствам фазового пространства и рассмотрим плоскость ( x, k_z/k ) (см. рис. 5 и 6). Величина k = —.J^ введена для нормировки. ^c

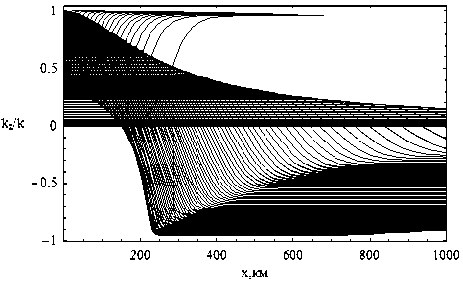
Рис. 5.

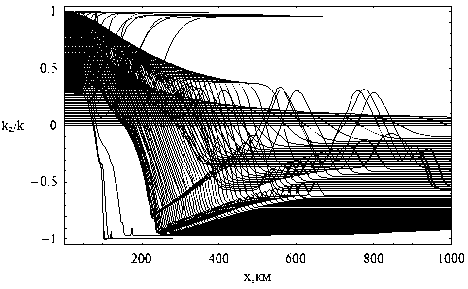
Рис. 6.

Лучевая структура в плоскости ( x, k_z / k ); невозмущенный случай – рис. 5; возмущенный случай – рис. 6

Рассмотрим сначала рис. 5 и проследим изменение характера лучевой траектории с ростом угла выхода луча (η). Все лучи выходят из точки с координатой x = 0. Луч с п = 0 идет строго горизонтально. Далее с увеличением начального значения kz (и соответственно η) лучи на рис. 5 поднимаются (относительно друг друга) и образуют верхнюю каустику, аналогичную верхней каустике рис. 3, но смещенную относитель- но неё. Отражаясь от ионосферного слоя, лучи выходят из плазмы и далее распространяются с постоянным kz. В верхней части рисунка видны лучи, прошедшие ионосферный слой. Следует отметить нижнюю каустику, образованную лучами, у которых сначала сильно уменьшилась компонента волнового вектора kz, а потом, после прохождения максимума слоя, опять возросла.

В возмущенном случае (рис. 6) лучевая картина принципиально похожа на структуру рис. 5, но, во-первых, в правой части рисунка мы наблюдаем сильные (но редкие) осцилляции, соответствующие распространению лучей в волновом канале и прерывающие каустику, во-вторых, имеют место и более слабые осцилляции, соот- ветствующие внутренним каустическим структурам рис. 4. И, наконец, следует отметить почти вертикальные лучи, не прошедшие ионосферный слой и опустившиеся на землю, что вызвано локальной неоднородностью. В целом каустическая структура рис. 6 весьма запутанная. Напрашивается вывод, что такая карта плохо пригодна для построения предканонического оператора, поскольку на ней трудно выбрать участок, не содержащий как свои особенности, так и особенности предыдущей карты. Хотя такое заключе- ние предполагает дополнительное исследование.

Рассмотрим теперь плоскость ( z, k_x/k ) (см. рис. 7 и 8).

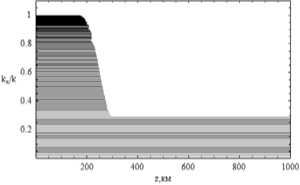
Рис. 7.

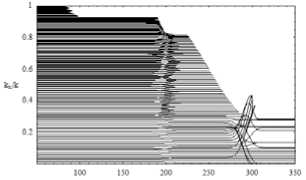
Рис. 8 а.

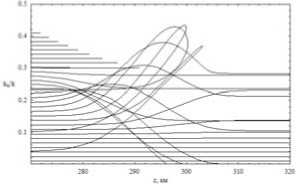
Лучевая структура в плоскости ( z, k_x / k ); невозмущенный случай – рис. 7; возмущенный случай – рис. 8; рис. 8 б – фрагмент рис. 8 а.

Рис. 8 б.

На рис. 7 показан невозмущенный случай.

Здесь всё просто. Нижние линии соответствуют лучам рис. 3, проходящим ионосферный слой, а выше мы видим лучи, отразившиеся от ионосферы. Причем, так как горизонтальные градиенты отсутствуют, лучи на этом рисунке возвращаются по тем же траекториям. Правая граница этих лучей – каустика. В возмущенном случае (рис. 8)

возникают вертикальные полосы, ограниченные каустическими линиями (рис. 8 а). Особый интерес представляет проявление локальной неоднородности в этом подпространстве (на этой карте) (см. фрагмент на рис. 8 б). Один из лучей даже делает петлю, охватывая неоднородность. Однако в целом лучевая структура на этой карте более регулярна, чем в предыдущем случае.

Перейдем теперь к чисто импульсному подпространству фазового пространства и рассмотрим плоскость ( k_x / k, k_z / k ) (см. рис. 9 и 10).

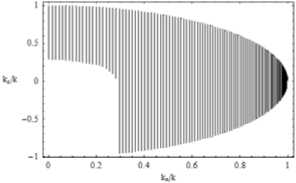
Рис. 9.

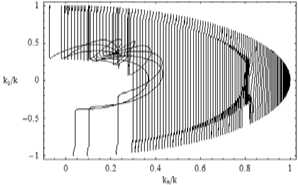
Рис. 10 а.

ВЕСТНИК 2015

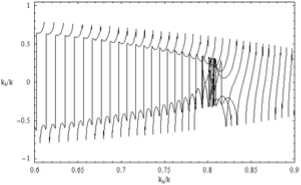
Лучевая структура в плоскости ( k_x / k, k_z / k ); невозмущенный случай – рис. 9; возмущенный случай – рис. 10; рис. 10 б – фрагмент рис. 10 а.

Рис. 10 б.

В невозмущенном случае (рис. 9) лучами являются прямые линии, поскольку для каждого угла выхода луча (η) kx является константой. Лучи, отражающиеся от ионосферы, идут сверху вниз и показаны в правой части рисунка. Проходящие лучи (слева) также идут сначала вниз, затем «отражаются» от уровня, соответствующего минимальной диэлектрической проницаемости среды (возникает каустика), и затем возвраща- ются обратно. Это наиболее, по нашему мнению, удачная карта, поскольку справа каустик нет, а слева справедлива геометрическая оптика: у проходящих лучей в плоскости (x, z) нет каустики, и можно вернуться в конфигурационное пространство.

Хуже обстоит дело в возмущенном случае (рис. 10). Во-первых, обращает на себя внимание локальная неоднородность в виде некоторой области слева, откуда во все стороны расходятся лучи (рис. 10 а), образующие, без сомнения, каустику. Во-вторых, в правой области имеется сложная лучевая, а следовательно, – и каустическая структура, фрагмент которой показан на рис. 10 б.

5. Лучевые расходимости

Наличие каустик и их особенностей приводит к сингулярностям лучевых решений, или подынтегральных выражений (для предканонического оператора Маслова). На рис. 11 и 12 показано ослабление электромагнитного поля вдоль лучей за счет расходимости лучевого потока.

в децибелах. В формуле (13) введены обозначения:

	∂ x ∂ ζ	∂ x ∂ η	- ∂Γ -∂ k x	∂Γ ∂ ω
J =	∂ y	∂ y	- ∂Γ	∂Γ	, J = J
	∂ ζ	∂ η	∂ k y	∂ ω	,     0        к = 100/
	∂ z	∂ z	-∂Γ	∂Γ
	∂ ζ	∂ η	-∂ k z	∂ ω

Таким образом, начальное значение якобиана вычисляется на расстоянии 1 м от изотропного

ВЕСТНИК 2015

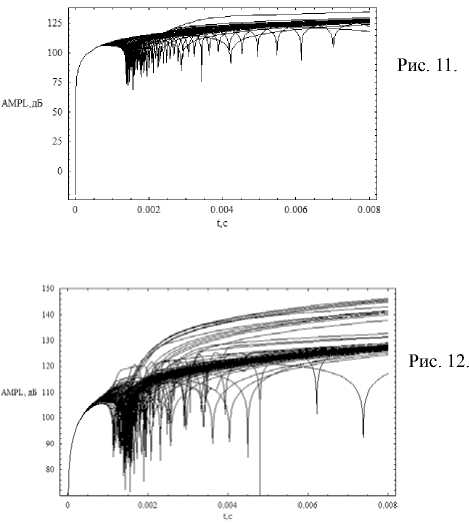
Зависимость расходимости сигнала от времени; невозмущенный случай – рис. 11; возмущенный случай – рис. 12.

передатчика.

Из рис. 11 видно, что вдоль луча интенсивность излучения сначала резко падает (для всех лучей), а потом выходит на относительно стабильный уровень (ослабление увеличивается, но медленно). При этом, поскольку каждый луч касается каустики, в её окрестности интенсивность сигнала резко возрастает (в лучевом приближении до бесконечности), и на графике возникают характерные «провалы». Самая большая расходимость у луча, близкого к «лучу Педерсена» (верхний луч).

В возмущенном случае (рис. 12) общая структура остается той же, но самыми слабыми

сигналами являются не только сигналы, передаваемые «лучами Педерсена», но и рассеянные локальной неоднородностью.

Рассмотрим теперь карту ( z, k_x ) и соответствующий коэффициент, пропорциональный

квадрату подынтегрального выражения для

предканонического оператора, выраженный в

децибелах:

AKX = - 20lg

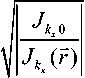
По горизонтальной оси отложено групповое время в секундах, а по вертикальной:

AMPL = - 20lg

J ₀

J ( r)

∂ k_x ∂ k_x ∂Γ ∂Γ ∂ ζ ∂ η ∂ x ∂ ω ∂ y ∂ y _-∂Γ ∂Γ ∂ ζ ∂ η ∂ k_y ∂ ω ∂ z ∂ z _-∂Γ ∂Γ ∂ ζ ∂ η ∂ k_z ∂ ω

J 0= J - (16) k x ⁰       k x t = 100/ c

Начальное значение якобиана J_{k 0} в (15) введено из соображений нормировки. На рис. 13 приведен график коэффициента (15) в зависимости от группового времени в невозмущенном случае.

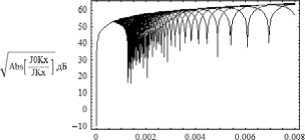
Рис. 13.

	∂ x ∂ ζ	∂ x ∂ η	- ∂Γ -∂ k x	∂Γ ∂ ω
Jkz =	∂ y ∂ ζ	∂ y ∂ η	∂Γ ∂ k y	∂Γ ∂ ω	, J к 0= J I • (18) k z 0        k z\ t = 100/ c      v 7
	∂ kz	∂ kz	∂Γ	∂Γ
	∂ ζ	∂ η	∂ z	∂ ω

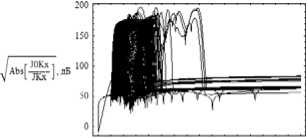
Рис. 14 а.

О 0.002       0.004       0.006       0.008

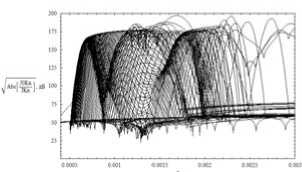
Амплитудный коэффициент J_{k 0} / J_k ;

невозмущенный случай – рис. 13; возмущенный случай –

Рис. 14 б.

рис. 14; рис. 14 б – фрагмент рис. 14 а.

Хотя абсолютные значения по вертикальной оси в два раза меньше, чем на рис. 11, структуры в целом похожи. Также имеют место провалы, обозначающие положение каустики или её особенности. На рис. 14 представлен возмущенный случай. Следует отметить, что хотя со временем все лучи выходят по этому коэффициенту на уровень 60–70 дБ (рис. 14 а), при прохождении возмущенной области они имеют значительные (до 200 дБ) колебания по ослаблению. Дольше

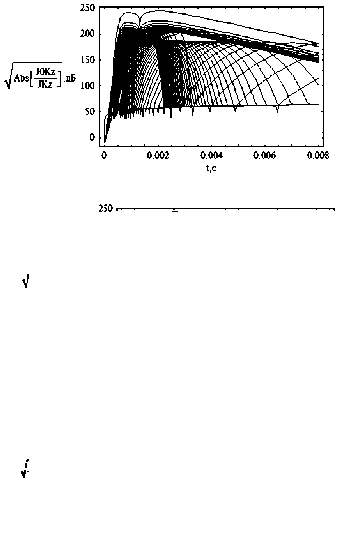
Рис. 15.

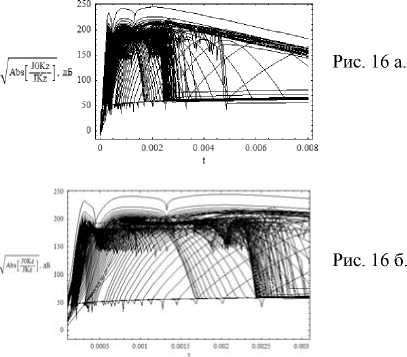
Амплитудный коэффициент J_{k 0} / J_k ;

невозмущенный случай – рис. 15; возмущенный случай – рис. 16; рис. 16 б – фрагмент рис. 16 а.

всех на этом уровне сохраняются лучи в волновом канале (рис. 14 б), однако после выхода из него коэффициент падает. Провалы в виде «бах-

ромы» показывают положения каустик.

На рис. 15, 16 приведены в децибелах графи-

ки зависимости ко эффици ента:

AKZ = - 20lg

J k z 0

J k_z ( r )

z

пропорционального квадрату подынтегрального выражения для предканонического оператора, для карты ( x, k_z ) вдоль лучей в зависимости от группового времени в невозмущенном и возмущенном случаях. В выражении (17)

Изучая рис. 15 и 16, видим, что коэффициент (17) увеличивается с ростом угла выхода луча η . Самые верхние лучи соответствуют рассеянию на локальной неоднородности, а наиболее темная часть в правой части рисунков – лучам, образующим каустическое остриё слоя F. Как и в предыдущем слое, свисающая вниз «бахрома» обозначает положение каустик.

Перейдем теперь к последнему случаю – карте ( k_x, k_z ). Коэффициент, пропорциональный квадрату подынтегрального выражения для предка-нонического оператора, для этой карты ( x, k_z ) в зависимости от группового времени имеет вид:

AKXZ = - 20lg

ВЕСТНИК 2015

где

∂ kx ∂ kx ∂Γ ∂Γ

∂ ζ  ∂ η   ∂ x ∂ ω

j = Sy  5 , ЭТ/ЭТ , J , .- J,,      . (20)

k x k z      dZ    дп      d ky/ d«      k x k z °      k x k z' t = 100/ c

∂ kz ∂ kz ∂Γ ∂Γ

∂ ζ  ∂ η   ∂ z ∂ ω

ВЕСТНИК 2015

На рис. 17 и 18 последовательно представлены невозмущенный и возмущенный случаи. Анализируя рис. 17, видим, что с увеличением угла выхода луча угол первоначального наклона траектории на рисунке растет, коэффициент вдоль траектории первоначально растет, а затем резко падает, и, наконец, крайний левый нисходящий луч соответствует каустическому острию. «Бахрома» отсутствует, зато коэффициент вдоль каждого луча стремится к -∞. Роль возмущений хорошо видна на рис. 18. Появляется «бахрома», так как возникают дополнительные каустики. Несколько круто спадающих траекторий справа соответствуют лучам из волнового канала. Верх- ние косые траектории связаны с рассеянием на локальной неоднородности.

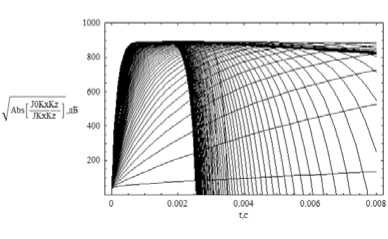
Рис. 17.

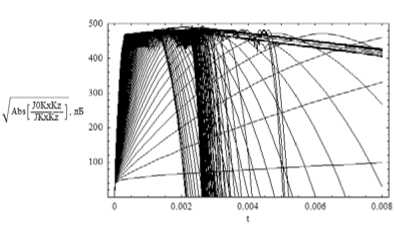
Рис. 18.

Амплитудный коэффициент J_{kk 0} / J_kk ; невозмущенный случай – рис. 17; возмущенный случай – рис. 18

• 6.    Заключение

Таким образом, в работе сопоставлены проекции 6-мерного фазового пространства в двумерные подпространства, соответствующие различ- ным картам канонического оператора Маслова, в невозмущенном и возмущенном случаях. Рассмотрены особенности (огибающие) лучевых семейств (каустики), возникающие в этих проекциях. С этой же целью в работе рассчитаны амплитудные множители вдоль лучей для разных карт и проанализированы сингулярности, связанные с касанием лучей каустик. В качестве возмущений ионосферного слоя F рассмотрены три дополнительные структуры: слой E, спорадический слой и локальное эллиптическое возмущение в окрестности максимума главного ионосферного слоя F. Необходимо подчеркнуть, что переход от классического представления решения в лучевой форме в конфигурационном пространстве к интегральному представлению (в частности, в виде канонического оператора Маслова) осуществляется ради построения равномерно асимптотического решения, и наличие каустик на канонических картах вблизи каустик конфигурационного пространства нежелательно. Рассмотренные подпространства даже в невозмущенном случае содержат каустики, а введение таких не очень сложных возмущений делает лучевую и каустическую картину весьма запутанной. Предпочтительнее всего в этом смысле выглядит переход в импульсное подпространство по двум переменным (координату y в данной задаче можно особо не выделять), но при этом увеличивается кратность интеграла, описывающего асимптотическое решение задачи.

Поэтому остается актуальной проблема тщательного анализа лучевых и каустических структур в конкретных задачах и перехода от интегрального описания к волновой теории катастроф [4–8; 22–25].

Хотя следует отметить, что сшивка различных канонических карт и непосредственное интегрирование также приводят к успешному решению [1–4; 12].