Исследование прохода через резонанс космического аппарата c изменяемой массовой асимметрией при спуске с малыми углами атаки в атмосфере Марса

Известно [1], что захват космического аппарата (КА) в длительный резонанс, может привести к существенному увеличению угла атаки и стать причиной аварийных ситуаций. Реализация резонансного режима движения наблюдается, например, вследствие увеличения угловой скорости возвращаемого космического аппарата от малых начальных до резонансных значений под воздействием механических моментов, обусловленных малыми значениям массовой и аэродинамической асимметрии [2, 3]. Влияние аэродинамической асимметрии существенно зависит от величин параметров атмосферы, в которой спускается космический аппарат.

В данной работе рассматривается движение космического аппарата в разряженной атмосфере Марса при малых углах атаки. Целью данной работы является исследование возможности обеспечения гарантированного прохода через резонанс космического аппарата посредством управления величиной малой массовой асимметрии.

• 2.    МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА

угла атаки α _п, аэродинамического угла крена ϕ _п и скоростного угла крена γ _а. При определении положения КА относительно центра масс также применяется система координат OXYZ [4]. В дальнейшем нижние индексы в этих углах ориентации не указываются.

Нелинейная низкочастотная система уравнений движения КА с малой массовой и аэродинамической асимметрией, описывающая движение КА относительно центра масс может быть представлена в виде [5]:

I x ^{d ω x} = -ε m _x ^A sin( θ + θ ₂ );

m^Ф_{x 0} qSLtg αω _1,2

F _a d α     ω ² tg α

=-Ψ -ε 4ω2 dt      4ω2π aa

4 ω ² I a

A

+ Е---- COS( 0 + 0 1 ) ;⁽¹⁾

2 ω _a

d θ

=ω -ω ; dt x1,2

d ω   ω dq

=ε .

dt 2q dt

Здесь ε – малый параметр; ω _x – угловая скорость КА относительно оси OX; θ=ϕ-π/2; Ψ=2πω^. /ω² = O (ε) ; m _x ^A , m^A , θ₁ , θ₂ – функции, определяющие величину и взаимное расположение аэродинамической и массовой асимметрий

2               ___ тАф =--(mxc+Cy Az) tga;

mzп sin 02 = -mXAi I mX ; cos 02 = mXA2 I mA ;

H2 2 / „ . 2 .         Ix ю ю a = Ilx tox 14 + ю ; ю1,2 =    x ±юa ;

^ю x - ^ю 1,2 - резонансная расстройка частот;

ю = ^- m_znqSLctg a I 1 ; L и S - длина аппарата и площадь миделевого сечения; q – скоростной напор; C_x , C_yп – коэффициенты аэродинамических сил; m_x^ф , m _y ^ф , m_z^ф – коэффициенты малых аэродинамических моментов от асимметрии формы КА; m_z^ф – коэффициент восстанавливающего аэродинамического момента, действующ ий в плоскости пространственного угла атаки; A y = A y I L , A z = A z IL ; D x , D y , D z - смещения центра масс КА в системе координат OXYZ ; I x = I_x I 1 ; I _x и I = I_y = I_z – моменты инерции КА относительно осей связанной системы координат ; F _a ( ю _x , a, q ) – известная функция. В системе уравнений не учитываются моменты аэродинамического демпфирования. Кроме того, момент от асимметрии формы m_x^ф может быть представлен в виде: т ф « т ф + т ф sin ф + т ^ф _с cos ф .

Система уравнений движения КА (1) решается совместно с тремя уравнениями, характеризующими движение центра масс осесимметричного КА [6]:

dV I dt = - CxvqS I m - g sin 9, d31 dt = -q(1 - V2I(R + H))cos31V, (2) dH I dt = V sin 3.

В уравнениях (2): C_xv ( a ) - аэродинамический коэффициент, определяемый из проекции вектора аэродинамической силы на направление воздушной скорости, ϑ – угол наклона траектории, m – масса КА, V – скорость КА, R – радиус Марса, H – высота полёта КА.

Космические аппараты, спускаемые в разряженной атмосфере Марса, как правило, имеют форму, представленную на рис. 1. Действующий на них аэродинамический момент может быть представлен формулой, содержащей две гармоники, зависящие от угла атаки [7]:

M _zn =-5 qSl ( C j sin ( a ) + C ₂ sin ( 2 a ) ) .

Главный резонанс в системе уравнений наблюдается при выполнении равенства: d 0 1 dt = ю _x - ю 1 ₂ = 0 . Из решения последнего уравнения получ ^, аем резонансное значение угло- r ω вой скорости ω ^r =±        .

‘    Vi- i x

С целью реализации прохода через резонанс

Рис. 1. Форма космического аппарата, спускаемого в атмосфере Марса введем в рассмотрение синусоидальный и экспоненциальный законы уменьшения параметра массовой асимметрии mxA :

m ^A = k 1 sm( 2 1 H ) ,             (3)

m xA = k ₂ e ^H .                (4)

Здесь k j ,k 2 и Xj , X2 - коэффициенты управления, Н - высота полета аппарата.

Наибольшее значение величины параметра асимметрии m_x ^A , при котором реализуется гарантированный проход через главный резонанс при малых значения угла атаки, может быть представлена в виде [3]

—A    lx   di ю I dt mx =                   .         (6)

4 1 - I x ^{ю a}

При расчете величины параметра асимме-A трии mx необходимо учесть значения переменных a, ю, dю I dt вычисленные на сепаратрисе, приведенные в работе [8] и справедливые при движении в разряженной атмосфере.

При атмосферном спуске происходит уменьшение высоты полёта H, что приводит (в соответствии с законами (3)-(4)) к уменьшению параметра массовой асимметрии m_x ^A . Если уменьшение параметра асимметрии m_x ^A достигает величины (6) и менее, то при малых углах атаки наблюдается гарантированный проход через главный резонанс.

• 3.    МОДЕЛИРОВАНИЕ СПУСКА КА

В АТМОСФЕРЕ МАРСА

ПРИ ЭКСПОНЕНЦИАЛЬНОМ И СИНУСОИДАЛЬНОМ

ЗАКОНАХ ИЗМЕНЕНИЯ АСИММЕТРИИ

При численном моделировании предполагалось, что космический аппарат (r = 0,25 м, Ix = 1кгм2, Iy = 5 кгм2, Iz = 5 кгм2) с массой 2 кг, длинной L = 1м и малой аэродинамической A асимметрией (m = 0.002, Сn1 = 2, Cn2 = -0,3) совершает спуск в атмосфере Марса (g0=3,86 м/с2 ,

R₀ = 3 390 км, H₀=100 км) при малых углах атаки (начальное значение угла атаки а ₀ = 9°).

Для оценки влияния законов управления асимметрией m_x^A выбраны такие показатели коэффициентов управления к 1 ,Х 1 и к 2 ,Я 2 , чтобы величины асимметрии m_x^A в начальный (t = 0) момент времени и момент времени окончания интегрирования (t = 400 c) были близки. Сравнение значений текущей угловой скорости КА и резонансного значения угловой скорости позволило определить, наблюдается ли проход через резонанс в каждом из рассматриваемых случаев.

Управление асимметрией КА с помощью синусоидального закона

управлении параметром его асимметрии m_x^A по закону, описывающему монотонную часть одной синусоидальной гармоники: m A = к 1 sin( 2 1 H )

Приняв Х 1 =10^-5 м ^-1, определим наличие резонансных эффектов, в зависимости от параметра k₁ .

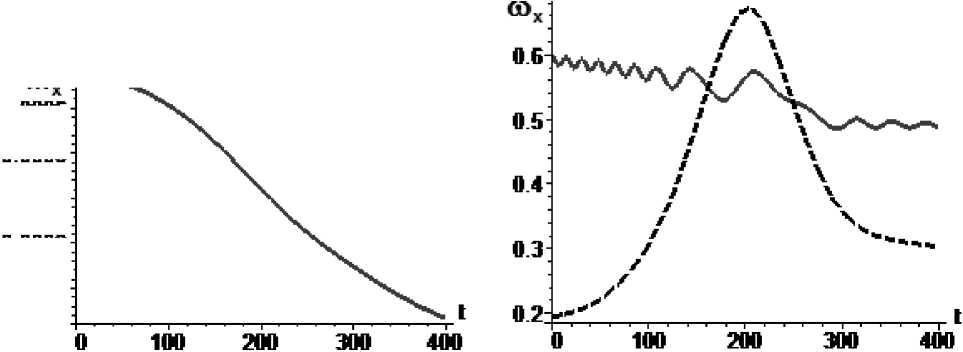
При значениях параметра к 1 = 8,08 - 10 ^{- 4} значение коэффициента асимметрии лежит в диапазоне m A е|^ 6,8 - 10 ^{- 4};1,3 - 10 ^{- 4}^| (рис. 2а). В этом случае наблюдается двойной проход через резонанс (рис. 2б). При значениях параметра к 1 = 2,93 - 10 ^{- 3} значение коэф -фициента асимметрии лежит в диапазоне m A е |^2,47 - 10 ³;4,8 - 10 - 4 ^ (рис. 3а). В этом слу-

Рассмотрим вначале поведение КА при

___А ие—

0.0004:

0.0003:

0.0002:

m A ( 0 ) = 6,8 - 10

. —4

а)

б)

по синусоидальному закону m A = 0,000808sin ( 0.00001 H ( t ) ) ,

"⁴, m A ( 400 ) = 1,3 - 10 ^{- 4} A

0.0006:

0.0005:

A

Рис. 2. Управление m _x

а – изменение параметра m _x во времени,

б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

а)

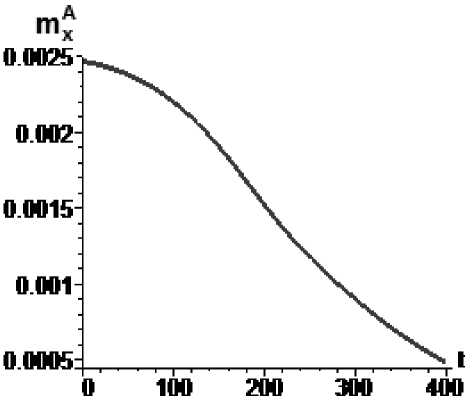
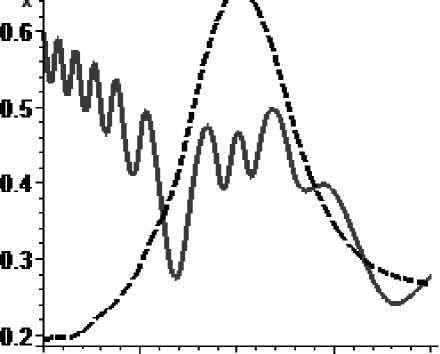
Рис. 3. Управление параметром

D 100    200    300    400

б)

m_x ^A по синусоидальному закону

mXA = 0,00293sin(0.00001H(t)), mA1 (0) = 2,47-10-3, mA1 (400) = 4,8-10-4 : а – изменение параметра mxA во времени, б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

чае наблюдается проход через резонанс на восходящей ветви резонансной кривой с захватом в резонанс на нисходящей ветви to rx (рис. 3б), что характеризует процесс увеличения вероятности захвата КА в резонанс.

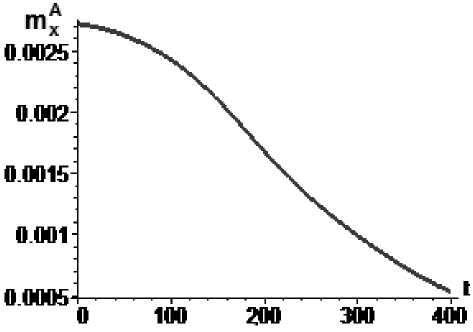
При значениях параметра к 1 = 3,23 - 10 ³ значения коэффициента асимметрии лежит в диапазоне m A е|^ 2,72 - 10 3 ;5,3 - 10 4 ^| (рис. 4а). При этом, наблюдается захват в длительный резонанс на восходящей ветви резонансной кривой to X и последующая реализация длительного резонанса в процессе всего рассматриваемого интеграла времени полета КА (рис. 4б). Следует отметить, что представленное поведение угловой скорости подтверждает вывод о том, что в случае управления параметром m_x^A по закону m X = 0,00293sin ( 0.00001 H ( t ) ) нижняя гра-

A

Рис. 4. Управление mx mX = 0,00323sin(0.00001H(t)), mA (0) = 2,72-10—3, mA (400) = 5,3-10—4 : а – изменение параметра mxA во времени, б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

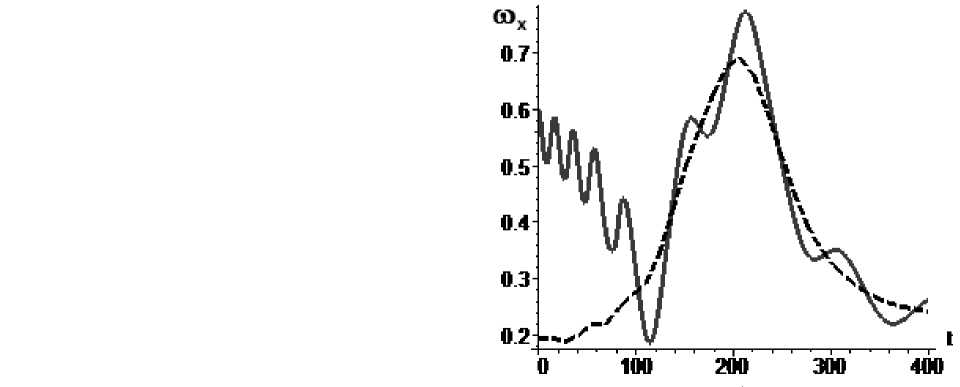
б) синусоидальному закону ( 0 ) = 3,40 - 10 ^{- 3} , m A ( 400 ) = 6,6 - 10 ^{- 4} :

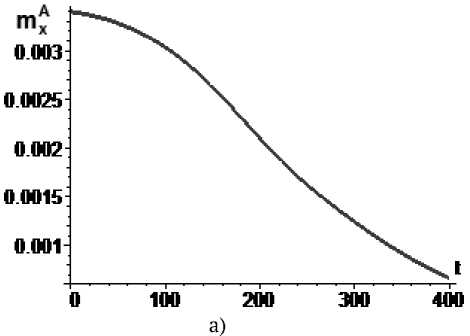
Рис. 5. Управление ^mx^A по m A = 0,00404sin ( 0.00001 H ( t ) ) , m A I

A а – изменение параметра mx во времени, б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

ница величин параметра k ₁ при котором происходит захват в резонанс равна к = 2,93 - 10 ^{- 3} . Повышение к 1 до значения к 1 = 4,04 - 10 ^{- 3} (значение коэффициента асимметрии лежит в диапазоне m A е|^ 3,4 - 10 ³;6,6 - 10 ⁴ ^| , рис. 5а) также показывает наличие резонансного движения (рис. 5б).

• 3.2.    Управление асимметрией КА с помощью экспоненциального закона

Рассмотрим вначале поведение КА при управлении параметром его асимметрии m_x^A по экспоненциальному: m A = к ₂ ехр( Л ₂ H ) .

синусоидальному закону

Приняв Х 1 =2 - 10 -5 м -1 , (что обеспечивает соответствие среднего уровня наклона графиков экспоненциального и синусоидального законов) определим наличие резонансных эффектов в зависимости от параметра k₂ .

При значениях параметра к2 = 9,2-10"5 значение коэффициента асимметрии лежит в диапазоне mA е|6,8•10"4;1,3•Ю"4| (рис. 6а). В этом случае наблюдается двойной проход через резонанс (рис. 6б). При значениях параметра к2 = 3,34•Ю"4 значение коэф -фициента асимметрии лежит в диапазоне mA е|2,47•10"3;4,6•Ю"4| (рис. 7а). В этом случае также наблюдается также двойной проход через резонанс (рис. 7б). В отличие от синусоидального закона управления, при экспо- ненциальном законе такой уровень асимметрии не приводит к захвату КА в резонанс (даже при большем времени снижения).

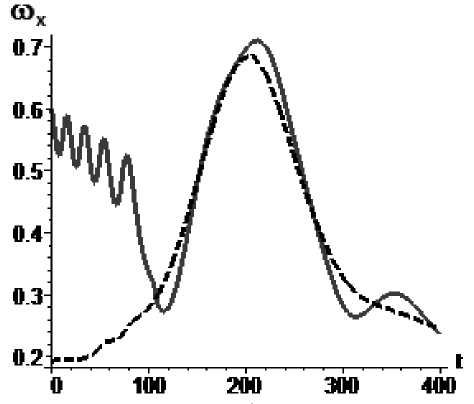
При значениях параметра к ₂ = 3,68 •Ю " ³ значение коэффициента асимметрии лежит в диапазоне m A е| 2,72 • 10 ^{- 3};5,1 - 10 ^{- 4} ^ (рис.8а),причем график поведения частот также демонстрирует отсутствие резонансных явлений (рис. 8б), в отличие от поведения КА при управлении асимметрией по синусоидальному закону. Начало резонансных явлений (рис. 9б) (которое можно принять за границу k₂ ) наступает в случае экспоненциального закона только при к ₂ = 4,6 • 10 " ⁴ , что соответствует значениям коэффициента асимметрии m_x^A , лежащим в диапазоне m A е | 3,4 • 10 ^{- 3}; 6,4 • 10 ⁴ I , (рис. 9а).

б)

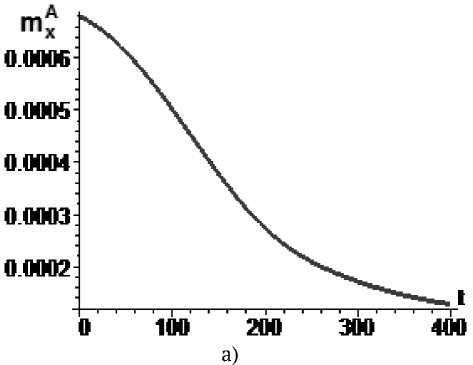
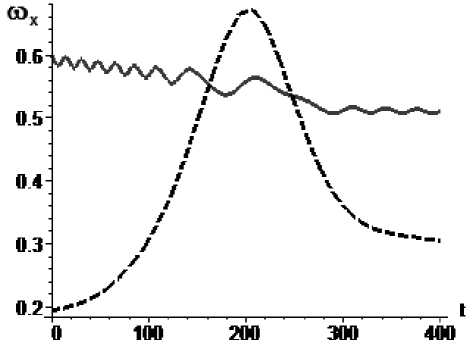
Рис. 6. Управление m_x по экспоненциальному закону

mA = 0,000092exp(0.00002H(t)), mA (0) = 6,8•Ю"4, mA (400) = 1,3•Ю"4: а – изменение параметра mxA во времени, б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

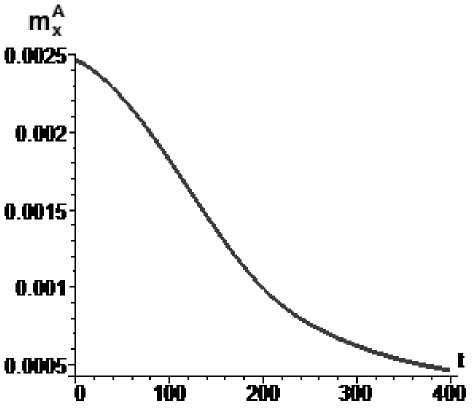
Рис. 7. Управление mxA по экспоненциальному закону mA = 0,000334 exp (0.00002H(t)), mA (0) = 2,47 -10"3, mA (400) = 4,6 -10"4 : а – изменение параметра mxA во времени, б – угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

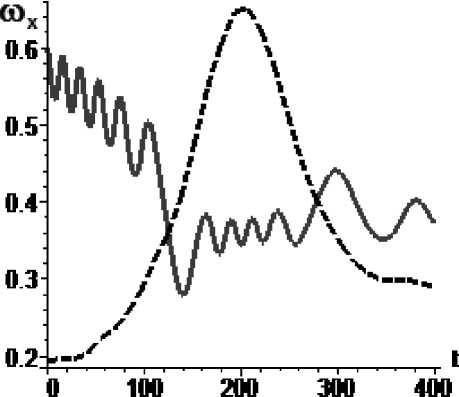
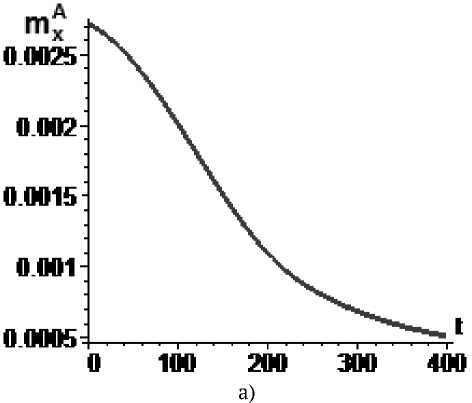
Рис. 8. Управление m x по экспоненциальному закону

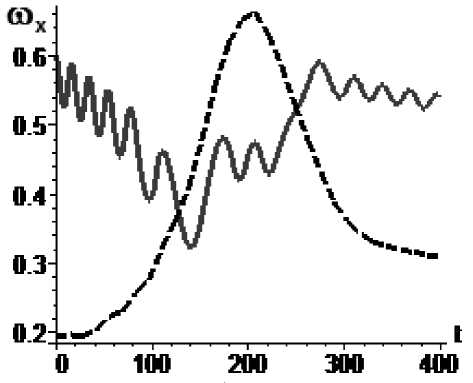
mA = 0,000368exp(0.00002H(t)), mXA (0) = 2,72-10-3, mA (400) = 5,1-10-4 : а - изменение параметра mA во времени, б - угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

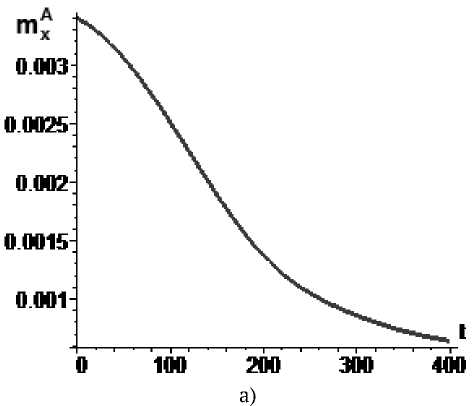
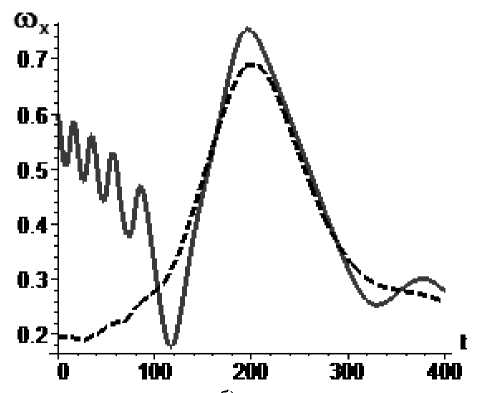
Рис. 9. Управление mx по экспоненциальному закону mX = 0,000460exp(0.00002H(t)), mA (0) = 3,40-10—3, mA (400) = 6,4-10—4 : а - изменение параметра mA во времени, б - угловая скорость КА (сплошная линия) и резонансное значение угловой скорости (пунктир)

ВЫВОДЫ

Численное моделирование случайного движения космического аппарата в окрестности резонанса позволяет сделать вывод о том, что выбор коэффициентов в законах управления параметром m A позволяет обеспечить гарантированный проход через резонанс.

Сравнение результатов численного моделирования для синусоидального и экспоненциального законов управления mxA показало, что экспоненциальный закон (по сравнению с синусоидальным законом) к резонансу позволяет достигнуть больших значений асимметрии mA, при котором реализуется проход через резонанс. При экспоненциальном законе управления наблюдаются меньшие значения параметра асимметрии mxA , что может являться причиной реализации прохода через резонанс. Однако, при синусоидальном законе управления в заключительной части полёта параметры асимметрии mx достигает меньших значений, чем при экспоненциальном законе. Данные закономерности непосредственно связаны с характером выпуклости экспоненциальной и синусоидальной функций.

Результаты работы представляют определенный практический интерес, так как в рассмотренной системе малое уменьшение величины асимметрии позволяет обеспечить реализацию нерезонансного вращения космического аппарата. Представленная работа относиться к классу задач, в которых изучается управление в системах с динамическим хаосом [9].