Исследование работы самонастраивающегося прогностического регулятора скорости вращения ротора синхронного генератора на киберфизической модели турбогенераторной установки

Киберфизические системы электроснабжения (КФСЭ) [1, 2] базируются на интеграции вычислительных систем в физические процессы. Концепция КФСЭ предполагает быструю и надежную интеграцию различных установок распределенной генерации (РГ) [3–5], которые могут работать как на традиционных [6, 7], так и на возобновляемых источниках энергии [8, 9]. Использование установок РГ в киберфизических электроэнергетических системах (ЭЭС) позволит уменьшить загрузку оборудования питающей сети, снизить потери на передачу электроэнергии, а также повысить надежность электроснабжения потребителей и качество электроэнергии [10, 11]. Однако для достижения лучшего эффекта от использования установки РГ в КФСЭ необходимо оптимально управлять генерирующим оборудованием в режиме реального времени.

Достаточно широкое распространение получили установки РГ, работающие на базе синхронных генераторов c автоматическими регуляторами возбуждения (АРВ) и скорости (АРС) вращения ротора. В связи с возможными возмущениями в КФСЭ оптимальные настройки этих взаимосвязанных регуляторов необходимо обеспечить для всех режимов работы установки РГ. Для снижения трудоемкости перенастроек можно использовать прогностические алгоритмы [12], обеспечивающие работу регулятора по рассчитанному прогнозу погрешности управления. Прогностические алгоритмы применяются в силовой электронике [13, 14], а также при управлении электродвигателями [15, 16]. В указанных работах используются сложные прогнозирующие модели с конечным набором управлений, требующие для реализации микропроцессорной техники и большого объема вычислений. В то же время достаточно просто реализуется прогнозирование с помощью линейной модели. Сравнение различных прогностических подходов к управлению, приведенное в работе [17], показывает, что линейные алгоритмы способны конкурировать с лучшими нелинейными. В работе [18] описан универсальный беспоисковый метод настройки линейных прогностических пропорционально-интегральнодифференциальных (ПИД) регуляторов. В статье [19] показано, что линейные прогностические ПИД-регуляторы могут эффективно использоваться в одноконтурной системе управления котлового пароперегревателя. В работе [20] показаны преимущества системы управления с модулем прогнозирования и даны рекомендации по выбору оптимального времени прогноза для регулирования теплового процесса. Результаты исследований на компьютерных моделях демонстрируют достаточно высокую эффективность линейных прогностических регуляторов для управления газотурбинной, турбогенераторной и гидрогенераторной установками РГ [21–24]. Однако для практического применения прогностических алгоритмов требуется проведение многочисленных исследований на более сложных компьютерных и физических моделях ЭЭС с установками РГ.

Ниже приводится описание самонастраивающегося прогностического регулятора скорости синхронного генератора, в котором постоянная времени линейного прогнозирующего звена определяется по резонансной частоте собственных колебаний ротора агрегата. Представлено описание киберфизической модели установки РГ и компьютерной модели предлагаемого самонастраивающегося прогностического регулятора, выполненной в пакете Simulink системы MatLab с использованием пакета Real Time Windows Target для управления физической установкой. Цель исследований состояла в определении эффективности применения самонастраивающегося прогностического регулятора в сравнении с типовым ПИД-регулятором в режимах подключения и отключения мощной нагрузки, а также короткого замыкания (КЗ).

Принцип работы самонастраивающегося прогностического регулятора скорости вращения ротора синхронного генератора

Использование алгоритма прогнозирования в составе регуляторов установок РГ (например, АРВ и АРС) позволяет осуществить их настройку с помощью одного параметра - времени прогноза. Линейный прогностический ПИД-регулятор представляет собой последовательное соединение двух звеньев: ПИД-регулятора и линейного прогнозирующего звена (ЛПЗ). Простой линейный прогноз может быть реализован по двум значениям регулируемой величины - текущему y(t ) и предыдущему y(t -A t ); при этом передаточная функция ЛПЗ определяется так [17]:

,

где T p – постоянная времени ЛПЗ (время прогноза); s – оператор Лапласа.

При возмущениях в ЭЭС возможен различный характер колебаний синхронного генератора установки РГ. Эти колебания вызывают отклонения напряжения в узлах и частоты в системе. Для устойчивости ЭЭС важно, чтобы колебания имели небольшую амплитуду и затухающий характер. Частота этих колебаний для синхронных машин зависит от синхронизирующих dP мощностей   , определяющих устойчивость, и постоянных механической инерции агрегатов, d5

от которых зависит быстрота протекания электромеханических процессов. Эта частота обычно называется собственной частотой колебаний и может быть определена из уравнения движения при малом изменении скорости вращения ротора и угла нагрузки генератора δ Δ [25]:

,                                                                            (2)

dt где J • toM - постоянная инерции; Ps - синхронизирующая мощность; 5A - изменение угла нагрузки генератора.

Для получения уравнения (2) в относительных единицах необходимо его разделить на номинальную мощность машины S _b . Тогда после некоторых преобразований из выражения (2) можно записать следующее соотношение [25]:

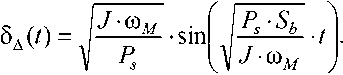
Из уравнения (3) видно, что угловая частота колебаний синхронного генератора равна

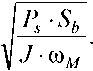
Это и есть собственная частота колебаний ω _p . Учитывая выражение из работы [25]

J " ^ММ _ ^

^b ^m можно записать

,                                                                                        (4)

№. E -U где Ps = —- = —---- • cos5 - синхронизирующая мощность; Eq - ЭДС генератора; Ug - напря-95 Xd жение генератора; Xd - индуктивное сопротивление генератора по продольной оси; Tje - эквивалентная постоянная механической инерции агрегата.

Частота собственных колебаний синхронного генератора согласно (3) задает характер изменения угла нагрузки 5, а синхронизирующая мощность влияет на амплитуду этих колебаний, что в целом определяет динамические свойства и устойчивость синхронной машины. Поэтому постоянную времени ЛПЗ при использовании в АРВ и АРС можно определить для номинальных величин как период собственных колебаний ротора агрегата, зависящий от угла нагрузки генератора δ, по выражению

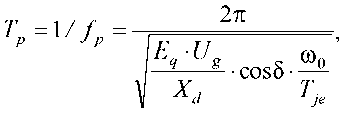
где f_p - частота собственных колебаний ротора генератора в Гц; ю₀ - номинальная угловая частота вращения ротора генератора в рад/с.

При изменении нагрузочного режима синхронного генератора изменяется угол δ, поэтому постоянную времени ЛПЗ целесообразно варьировать, т. е. возможно создать самонастраивающийся прогностический АРС. Его структурная схема представлена на рис. 1. Необходимо отметить, что функция fp (δ) зависит от параметров агрегата и для различных установок РГ будет отличаться.

Описание киберфизической модели турбогенераторной установки

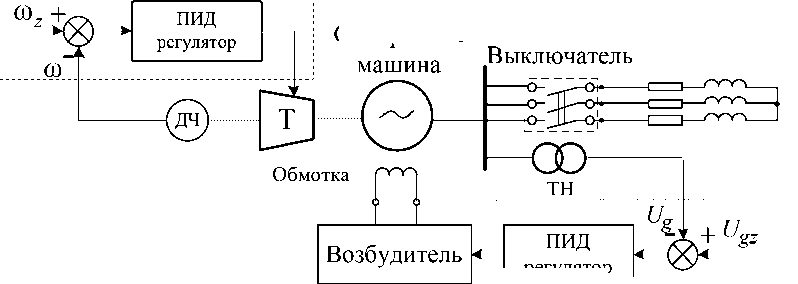
Проверка эффективности работы самонастраивающегося прогностического регулятора скорости проводилась на киберфизической модели турбогенераторной установки, схема которой показана на рис. 2. Модель состояла из генератора, приводимого во вращение первичным двигателем – турбиной, в качестве которой использовалась машина постоянного тока. В состав дополнительного оборудования входили следующие элементы: источник питания машины постоянного тока, используемый для ручного или автоматического управления; возбудитель синхронной машины с такими же возможностями; преобразователь угловых перемещений;

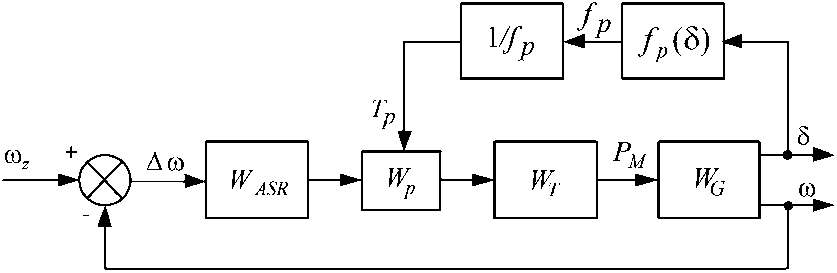
Рис. 1. Структурная схема самонастраивающегося прогностического регулятора скорости: W_G – передаточная функция генератора; W T – передаточная функция турбины; W ASR – передаточная функция АРС (ПИД-регулятор); W_p – передаточная функция линейного прогнозирующего звена (1); ω _z – заданное значение скорости вращения ротора генератора; P M – механическая мощность на валу турбины

Fig. 1. Structural diagram of a self-adjusting predictive speed controller: W G – generator transfer function; W T is the transfer function of the turbine; W_ASR – ASR transfer function (PID controller); W_p is the transfer function of the linear predictive link (1); ω z is the set value of the generator rotor speed; P M – mechanical power on the turbine shaft

Активно-

Синхронная индуктивная нагрузка

MatLab, Simulink, Real-Time Windows Target возбуждения

регулятор

MatLab, Simulink, Real-Time Windows Target

Рис. 2. Схема киберфизической модели установки РГ: Т – турбина; ТН – трансформатор напряжения; ДЧ – датчик частоты вращения

Fig. 2. Scheme of the cyber-physical model of the DG plant: Т – turbine; VT – voltage transformer; SS – speed sensor активная и индуктивная нагрузки. Номинальные параметры электрических машин представлены в табл. 1.

При моделировании генератор работал на активную нагрузку мощностью 18 Вт. В качестве возмущений рассматривалось подключение и отключение активно-индуктивной нагрузки мощностью 50 + j 30 В·А.

Регулирование напряжения и скорости вращения ротора генератора выполнялось автоматически с помощью цифровых ПИД-регуляторов с временем дискретизации 0,0019532 с, реализованных в пакете Simulink. Схемы моделей этих регуляторов приведены на рис. 3 и 4. В отличие от схемы приведенного самонастраивающегося прогностического регулятора скорости (рис. 4) обычный АРС представляет собой ПИД-регулятор без ЛПЗ. Связь между физической – 182 –

Таблица 1. Номинальные параметры спаренных электрических машин

Table 1. Ratings of coupled electrical machines

Параметр / Parameter	Значение / Value
Синхронная машина / Synchronous machine
Номинальная активная мощность P n / Rated active power P n	100 Вт / W
Коэффициент мощности cosφ / Power factor cosφ	1
Номинальное напряжение U n / Rated voltage U n	220 В / V
Номинальный ток обмотки статора I n / Rated stator winding current I n	0,24 А
Схема соединения обмотки статора / Stator winding connection diagram	Y 0
Номинальная частота вращения ротора n / Rated rotor speed n	1500 об/мин / rpm
Номинальное напряжение возбуждения U f / Rated excitation voltage U f	21 В / V
Номинальный ток возбуждения I f / Rated field current I f	1,75 А
Машина постоянного тока / DC machine
Номинальная мощность Pn / Rated power Pn	90 Вт / W
Номинальное напряжение якоря U a / Rated armature voltage U a	220 В / V
Номинальный ток якоря I a / Rated armature current I a	0,56 А
Номинальное напряжение обмотки возбуждения U f / Rated field voltage U f	220 В / V
Номинальный ток обмотки возбуждения I f / Rated field current I f	0,2 А
Номинальная частота вращения n / Rated speed n	1500 об/мин / rpm
Маховик / Flywheel
Момент инерции / Moment of inertia	0,009 Н×м×с2 / N×m×s2

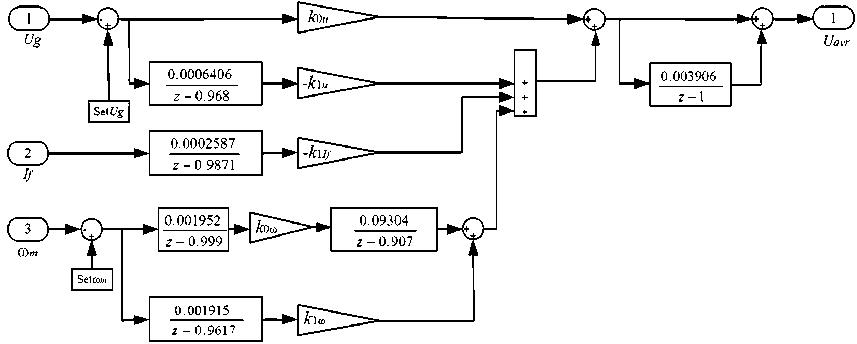
Рис. 3. Структурная схема модели цифрового АРВ: Set U_g – заданное значение напряжения генератора; ω _m – текущее значение скорости ротора генератора; Setω _m – заданное значение скорости ротора генератора; k _{0 u} , k _{1 u} , k _{1 I} f , k _0ω, k _0ω – коэффициенты настройки АРВ

Fig. 3. Structural diagram of the digital AVR model: Set U g – generator voltage set value; ω m is the current value of the generator rotor speed; Setω m – set value of generator rotor speed; k 0 u , k 1 u , k 1 If , k 0ω , k 0ω – AVR tuning coefficients

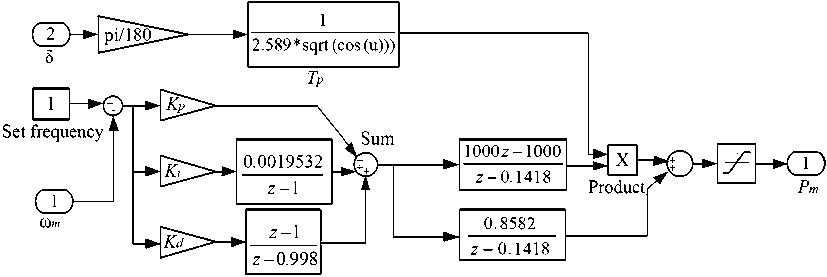
Рис. 4. Структурная схема модели цифрового самонастраивающегося прогностического АРС: K p , K i , K d -коэффициенты настройки АРС

Fig. 4. Structural diagram of the digital self-adjusting predictive ASR model: K p , K i , K d – ASR tuning coefficients

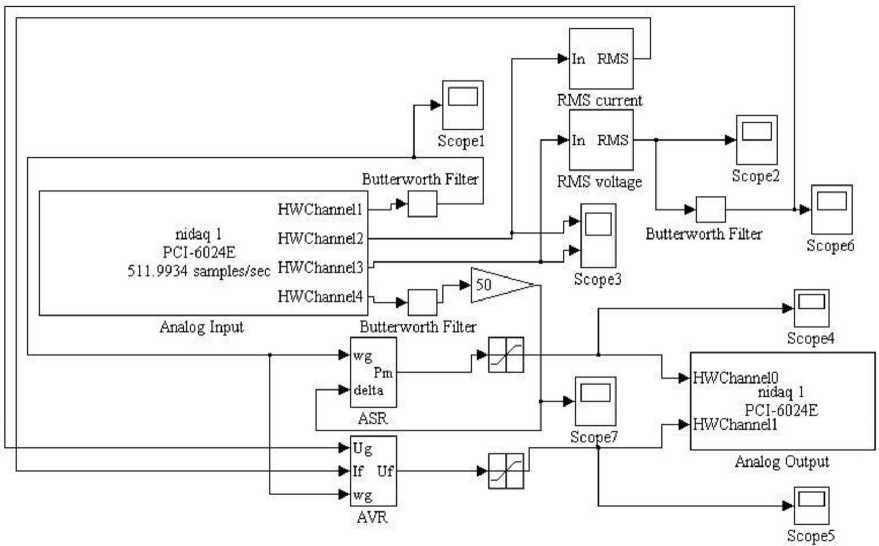
Рис. 5. Схема цифровой модели управления физической установкой

Fig. 5. Scheme of the digital control model for the physical installation моделью и компьютером осуществлялась через плату ввода-вывода типа PCI 6025Е. Информация о параметрах системы поступала от блока Analog Input, а управление производилось с помощью блока Analog Output пакета Real-Time Windows Target системы MatLab. Используемая схема управления показана на рис. 5. Для удаления шума перед подачей сигналов в регуляторы использовались дискретные фильтры Баттерворта (блоки Butterworth Filter на рис. 5). Это значительно улучшало качество управления и точность определения времени прогноза в самонастраивающемся прогностическом АРС.

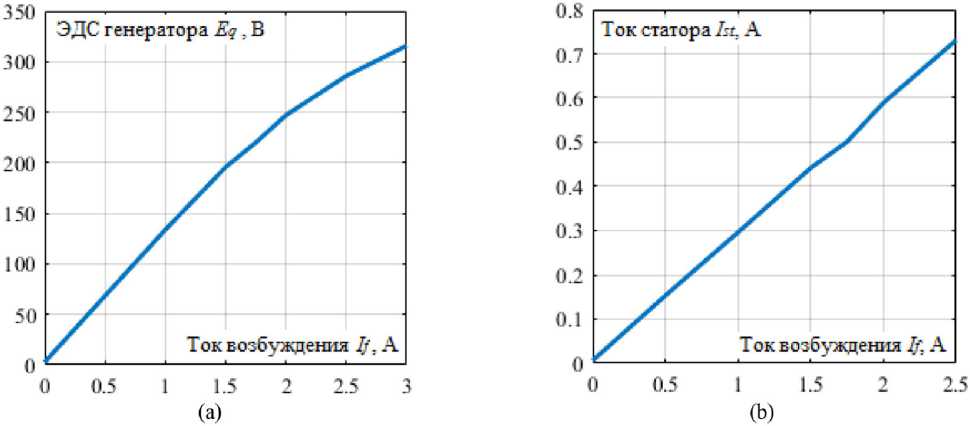
Рис. 6. Экспериментальные характеристики режимов ХХ (а) и КЗ (б) синхронного генератора: ЭДС E q определялась как линейное напряжение

Fig. 6. Experimental characteristics of idling (a) and short circuit (b) modes of a synchronous generator: EMF E q was determined as a linear voltage

Индуктивное сопротивление генератора по продольной оси было определено экспериментально по результатам опытов холостого хода (ХХ) и короткого замыкания (КЗ) (рис. 6) для тока возбуждения I f = 1,5 A и составило для фазных величин X d = 0,483 о. е.

В соответствии с приведенными параметрами машин постоянная времени ЛПЗ самонастраивающе гося АРС для физической модели установки РГ определялась по выражению (рис. 4).

Результаты моделирования и основные выводы

Исследования проводились для режимов подключения и отключения мощной нагрузки, а также для удаленного кратковременного трехфазного КЗ, возникающего в конце присоединенной к генератору линии с сопротивлением Z =116 + j 94,2 Ом. В этих режимах выполнялось сравнение работы обычного и самонастраивающегося прогностического АРС; при этом рассматривались следующие настройки регуляторов:

• 1)    согласованная настройка АРВ и АРС [11]: для АРВ k ₀ u =10, k 1 u =5, k 1 f =0, k _0m=0,15, k _0m=0,05; для АРС K p = 1, K i = 0,5, K d = 0;

• 2)    несогласованная настройка АРВ и АРС: для АРВ k ₀ u =1, k 1 _u =1, k 1 f =0, k _0ю=1, k _0ю=1; для АРС K p = 1, Kt = 1, K d = 1.

Результаты моделирования режимов подключения и отключения мощной нагрузки для согласованной настройки регуляторов представлены на рис. 7 в виде временных зависимостей скорости вращения ротора синхронного генератора. Полученные результаты позволяют сделать вывод об улучшении показателей качества управления при использовании самонастраивающегося прогностического АРС: в режиме подключения нагрузки уменьшился максимальный провал скорости ротора на 34 % (рис. 7 а ); в режиме отключения нагрузки на 28 % снизилась величина перерегулирования скорости ротора генератора, а также колебательность регулируемых параметров (рис. 7 б ).

Результаты моделирования режимов подключения и отключения мощной нагрузки для несогласованной настройки регуляторов представлены на рис. 8 и 9.

В режиме подключения дополнительной нагрузки для несогласованно настроенных регуляторов самонастраивающийся прогностический АРС позволил получить следующие положительные результаты: на 33 … 34 % снизились провал и перерегулирование скорости (рис. 8 а ); на 21 % уменьшилось перерегулирование напряжения (рис. 8 б ).

Подобный эффект наблюдается и при отключении мощной нагрузки. Удалось снизить следующие показатели: перерегулирование скорости ротора генератора на 34 % (рис. 9 а ), а провал напряжения на 13 % (рис. 9 б ). Однако при этом несколько увеличилась колебательность скорости (рис. 9 а ). Это может быть связано с резким уменьшением времени прогноза при сбросе нагрузки, которое нужно ограничивать. Поэтому в дальнейших исследованиях необходимо рассмотреть влияние на процесс регулирования резкого изменения времени прогноза.

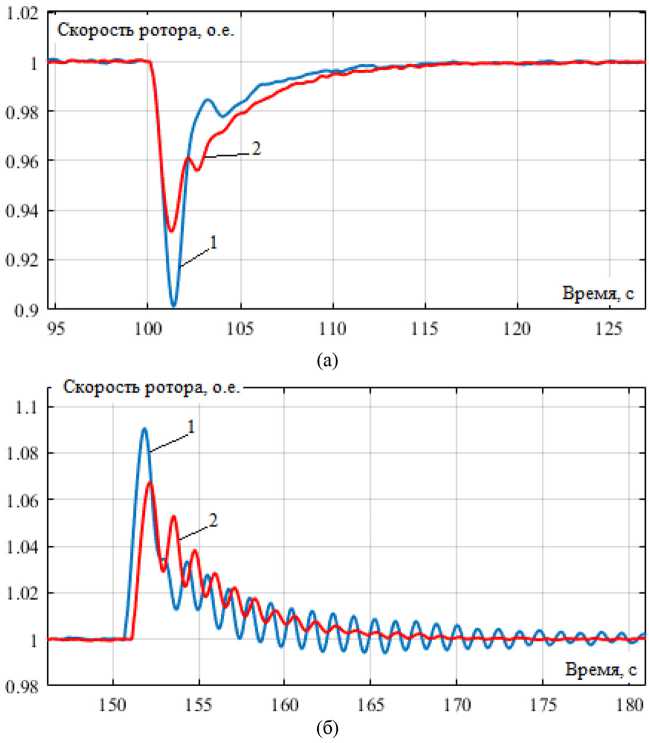
Рис. 7. Скорость вращения ротора генератора для согласованной настройки регуляторов при подключении (а) и отключении (б) мощной нагрузки: 1 – обычный АРС (ПИД-регулятор); 2 – самонастраивающийся прогностический АРС

Fig. 7. The generator rotor speed for the coordinated adjustment of the regulators when connecting (a) and disconnecting (б) a powerful load: 1 – conventional ASR (PID controller); 2 – self-adjusting prognostic ASR

Результаты моделирования удаленного КЗ длительностью 1 с представлены на рис. 10, на котором видно, что использование самонастраивающегося прогностического регулятора дает возможность снизить в 1,3 раза провал и уменьшить в 2,6 раза перерегулирование скорости после отключения КЗ (рис. 10).

В целом результаты моделирования показывают достаточно высокую эффективность применения предлагаемого самонастраивающегося прогностического регулятора в нормальных, аварийных и переходных режимах; при этом основной положительный результат заключается в улучшении показателей качества процесса управления.

В дальнейшем необходимо проведение исследований, направленных на разработку прогностического АРВ и испытание его работы совместно с АРС аналогичного типа на кибер-физической модели турбогенераторной установки. Кроме того, требуется выполнение работ по определению влияния резкого изменения времени прогноза предлагаемых прогностических регуляторов.

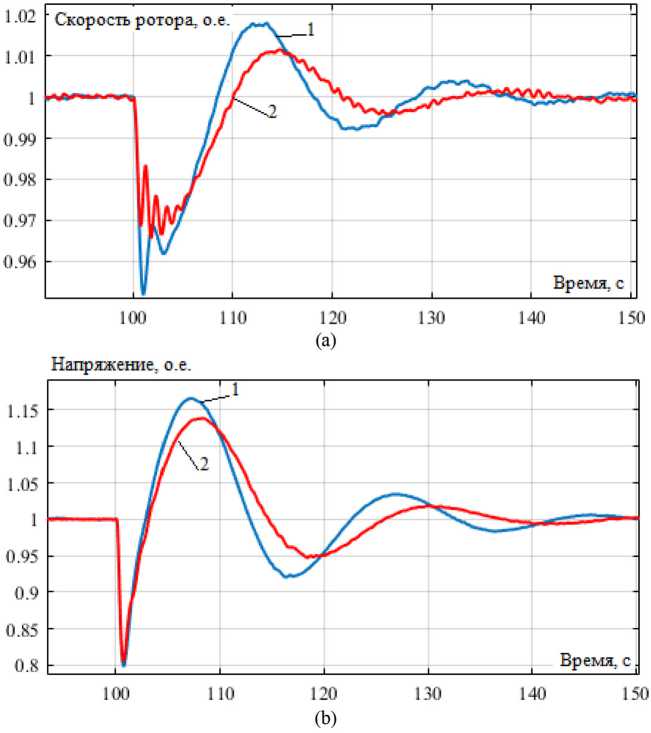
Рис. 8. Скорость вращения ротора (а) и напряжение генератора (b) для несогласованной настройки регуляторов при подключении мощной нагрузки: 1 – обычный АРС (ПИД-регулятор); 2 – самонастраивающийся прогностический АРС

Fig. 8. Rotor speed (a) and generator voltage (b) for inconsistent adjustment of regulators when a powerful load is connected: 1 – conventional ASR (PID controller); 2 – self-adjusting prognostic ASR

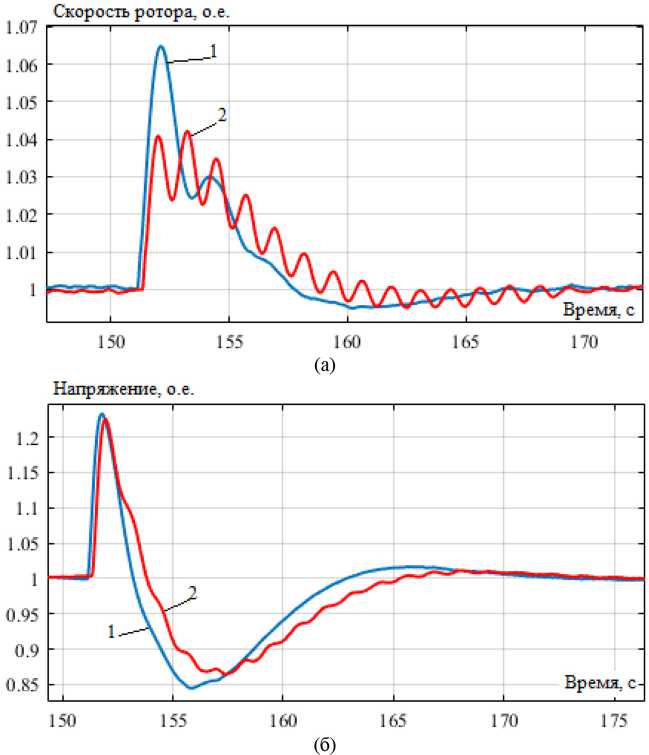
Рис. 9. Скорость вращения ротора (а) и напряжение генератора (б) для неоптимальных настроек регуляторов при отключении мощной нагрузки: 1 – обычный АРС (ПИД-регулятор); 2 – самонастраивающийся прогностический АРС

Fig. 9. Rotor speed (a) and generator voltage (b) for non-optimal regulator settings when a powerful load is turned off: 1 – conventional ASR (PID controller); 2 – self-adjusting prognostic ASR

Заключение

Представлено описание киберфизической модели установки РГ и компьютерной модели предлагаемого самонастраивающегося прогностического регулятора скорости вращения ротора генератора для управления физической установкой. Результаты моделирования нормальных и аварийных режимов позволяют сделать следующие выводы:

• 1.    Самонастраивающийся прогностический регулятор скорости более эффективно работает по сравнению с типовым ПИД-регулятором в нормальных, аварийных и переходных режимах даже без решения задачи его оптимальной настройки. Основной эффект от его применения заключается в улучшении показателей качества процесса управления. В рассмотренных режимах провал скорости ротора генератора снижался на 34 %, перерегулирование скорости уменьшалось на 32 %.

• 2.    Использование самонастраивающегося прогностического регулятора скорости позволило улучшить управление напряжением на зажимах генератора: при подключении мощной

• 3.    Предлагаемый цифровой самонастраивающийся прогностический регулятор может использоваться для повышения устойчивости, адаптивности и живучести установок распределенной генерации, работающих в составе киберфизической системы электроснабжения.

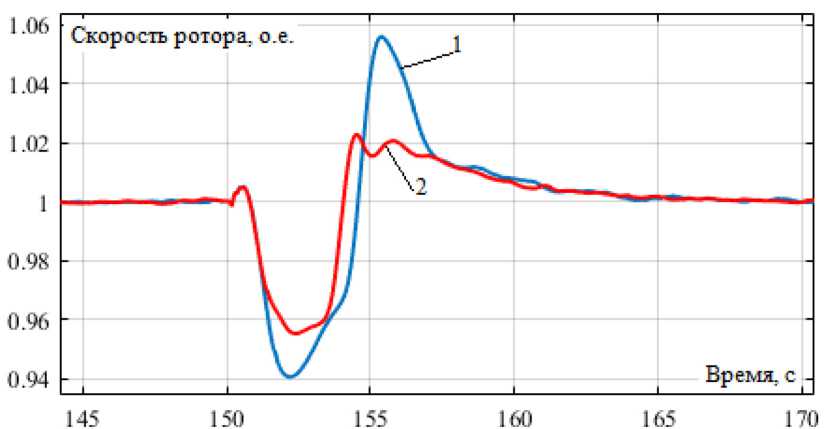
Рис. 10. Скорость вращения ротора синхронного генератора для согласованной настройки регуляторов при кратковременном трехфазном КЗ: 1 – обычный АРС (ПИД-регулятор); 2 – самонастраивающийся прогностический АРС

Fig. 10. The rotor speed of the synchronous generator for the coordinated adjustment of the regulators in case of a short-term three-phase short circuit: 1 – conventional ASR (PID controller); 2 – self-adjusting prognostic ASR нагрузки перерегулирование напряжения уменьшалось на 21 %; при отключении нагрузки провал напряжения снижался на 13 %.