Исследование распределения локальных напряжений атомного графен

1. Молекулярно-механическая модель графена. Модуль Юнга

Эмпирическая модель графена основывается на теории валентного силового поля с учетом взаимодействия Ван-дер-Ваальса несвязанных атомов. Полная энергия E_tot финитного графенового листа представляется многочленом, каждая составляющая которого имеет свой весовой коэффициент, определяемый в результате обработки экспериментальных данных:

E ot = ^

K r ( r - r 0 )

+x

K и^(и - ^и0 ) ⁺

+

Z (>

^K 6 ^{b ) .}

r

Первая сумма (суммирование ведется по всем химическим связям) есть энергия изменения длин связей в наноструктуре по отношению к длине связи в графите ( r ₀ = 1,42 Е); вторая сумма (суммирование проводится по всем валентным углам) – энергия изменения валентных углов между химическими связями по отношению к углу между связями в графите ( 9 0 = 120 ^о ); третья сумма (суммирование ведется по всем па-

рам не связанных химически атомов) – энергия взаимодействия Ван-дер-Ваальса (потенциал Леннарда-Джонса); К_г , К ₉ , K a , K b - весовые коэффициенты. Такой способ задания полной энергии наноструктуры был выбран как один из наиболее оптимальных. Действительно, здесь учтены энергия химических связей и валентных углов, а также энергия несвязанных атомов. Увеличение числа энергетических компонентов в формуле (1) приведет к возрастанию количества неизвестных весовых коэффициентов и, как следствие, усложнению процесса параметризации модели (поиска весовых коэффициентов).

Весовые коэффициенты подобраны в результате сравнения расчетных данных с экспериментальными [1]:

К = 3,25 - 10 2 ж К _в = м

= 4,4 - 10 ^{- 19} - ДЖ -, К _а = рад ²

= 4,0 - 10 " ¹³⁹ ДЖЖ , К _ь =

м

= 1,5 - 10 - 80 ДЖ .                    (2)

м ⁶

Модифицированная эмпирическая модель позволяет рассчитывать атомную структуру углеродного кластера с удовлетворительной точностью: погрешность составляет менее 3 %.

Модуль Юнга определяется выражением E = T / S x ( L / A L ), где сила растяжения (сжатия) T вычисляется по величине энергии упругого растяжения (сжатия) A E : A E = T x A L /2; L – длина недеформированного атомного каркаса, A L - удлинение каркаса. Площадь S рассчитывается как площадь края шириной 3,4 Е (расстояние между слоями в графите).

Рассмотрим устойчивость прямоугольной пластинки размером a x b ( a и b - размеры вдоль осей X , Y ), сжимаемой в направлении X . В этом случае граничные условия примут вид:

x - 0, x - a , w - 0, M_x - 0

x у - 0, у - b, w - 0, My - 0,       (5)

2. Расчет локальных напряжений атомного каркаса в рамках теории сплошной среды

где M_x и M_y – главные моменты относительно осей х и у .

Функцию прогиба будем искать в виде:

Графеновый лист представляется нанопластиной с ортотропией механических свойств. Для расчета распределения локального напряжения атомной сетки однослойного графена применяется теория устойчивости для пластинок. Такой подход является некоторым приближением, использующим, с одной стороны, эмпирический подход для расчета энергии деформации и модулей упругости, с другой стороны, методику теории упругости пластин.

Функция прогиба нанопластины w имеет вид [2]:

рx   рy w (x, у) - F sin —sin —, ab где начальная функция представлена гично:

рx   рy w0 (x, y) - F Sin—sin —.

^{0    0} ab

анало-

Величины F и F ₀ соответствуют значениям функций в середине пластинок.

В результате подстановки (7) и (8) в (4) получаем:

D + 2 D₃

¹ д x^{4        3}

д4 w d 94 w дx2dy2     2 dy 4

д ²( w о + w )

T x     9x 2

( D 1 £ 4 + 2 D 3^-2 + 2 D 2 р 4 ) F - a ⁴         a ² b ²         b ⁴

- T x [ F o + F ^р ^ .                       (8)

a

где      Тx – приложенная к телу сила вдоль оси х (усилия вдоль осей y и z отсутствуют, то есть Тy = Тz=0); w0 – начальная функция прогиба;

D ₁, D ₂, D ₃ – жесткости, вычисляемые по формулам:

Преобразуя это выражение и введя новую константу D - n ²[ D 1 ^- + 2 D ₃ ^- + D ₂ a— ], получа- a bb ем выражение для параметра F :

T F

F - T x F ⁰ .

D - T

x

D -    ^E 1 h³   , D =    ^E 2 h³   ,

¹   12(1 - 9 , 9 2 )     ²    12(1 - 99 2 )

Функцию прогиба запишем в виде:

Gh ³

^D 3 - D_n ^{+ 2 D} 66 ^{- 9} 2 D + 12 ,

TF    рx  рy w - —x—°-sin —sin —.

D - T_x   a    b

где E ₁ и E ₂ – модули Юнга по направлениям осей х и y ;

ϑ ₁ и ϑ ₂ – коэффициенты Пуассона по

Нормальные напряжения о 1 по направлению X в каждой точке поверхности пластинки (то есть в окрестности каждого атома графена) определяются выражением:

направлениям x и y ;

G – модуль сдвига; h – толщина пластинки.

6 D, д ² w   _п д² w.

у1  --71(--- Т + 9 --у).

¹       h ² д x ^{2     1} д у ²

После подстановки (11) в (12) получаем окончательную формулу для напряжений:

рx   рy у1 = 5 sin —sin , ab где 5 = 6DTFM^ + 5^).

h ² D - T_x a ^{2    1} b ²

x

Рассмотрим графеновый фрагмент с 78-ю атомами, показанный на рисунке 1.

Фрагмент графена имеет геометрические размеры: a = 66,42 Е; b = 19,88 Е; толщина нанопластины принимается равной h = 3,4 Е. Рассчитанные с помощью молекулярно-механической модели графена (см. п. 1) модули Юнга равны Е1 = 0,99 TПа; Е2 = 0,81 ТПа, коэффициенты Пуассона - 51 = 0,27, 52 = 0,2. Найденные параметры упругости хорошо согласуют- ся с известными эксперимента и расчетными расчетов [3; 4]: модуль Юнга ~1 ТПа; коэффициент Пуассона 0,12–0,413.

По вычисленным параметрам упругости определены жесткости графенового листа: D ₁ = 2,79 ТПа* Е ³ ; D ₂= 3,06ТПа* Е ³ ; D ₃ = 2,64 ТПа* Е ³ ; D = 0,8 нН. Начальные деформации отсутствуют, следовательно F ₀ = 1.

Для деформированного листа, подвергнутого сжатию на 5 % в направлении X , рассчитано распределение локального напряжения вблизи каждого атома с помощью формулы (13). Для подобной деформации понадобилось бы усилие T_X = 1,98 нН; S = 1,49 ТПа. Значение напряжения вблизи каждого атома было найдено подстановкой его координат в (13). Распределение относительного локального напряжения o * = о / 5 представлено на рисунке 2.

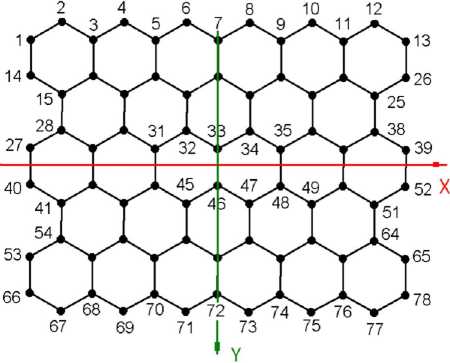
Рис. 1. Графеновый фрагмент

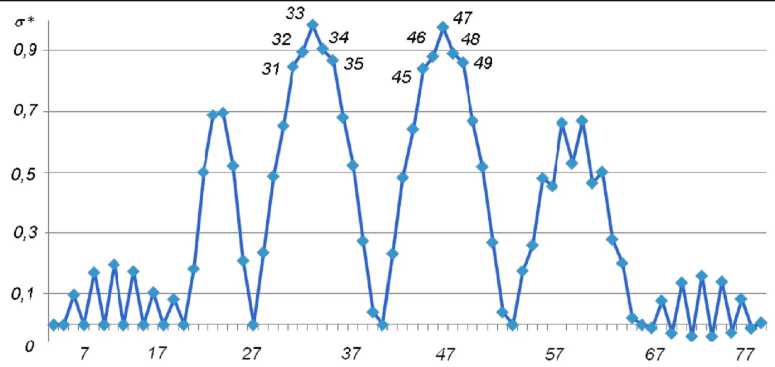
Рис. 2. Зависимость о * от номера атома

VT1,6 ТПа

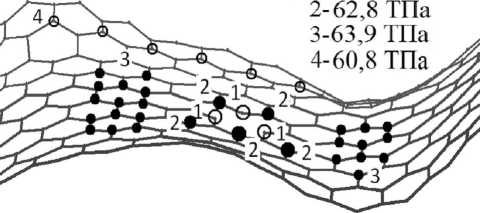
Рис. 3. Фрагмент графеновой наноленты, подвергнутой сжатию на 20 % от первоначальной длины

Можно предположить, что проведенный в рамках теории сплошной среды анализ распределения локального напряжения позволит прогнозировать, какие атомы будут элиминировать из графенового листа при последующем увеличении деформации.

• 3.    Расчет локальных напряжений атомного каркаса в рамках молекулярно-механической модели графена

В рамках молекулярно-механической модели локальное напряжение в окрестности i -го атома графена рассчитывается по формуле:

у i = atom / V i .              (13)

Выражение (13) для напряжения представляет собой отношение энергии взаимодействия данного атома c окружением к объему, который рассчитывается с учетом величины ван-дер-ваальсового радиуса атома.

Были исследованы графеновые наноленты шириной 2–3 нм при различных длинах. Напряжение недеформированной наноленты в центральной части структуры составляло 58,65 ГПа, а по краям 40,6 ГПа. Это связано с тем, что краевые атомы имеют по два свободных электрона, следовательно, энергия этих атомов выше.

При сжатии графеновой наноленты на 1–20 % наблюдается возрастание локальных напряжений. На рисунке 3 представлен фрагмент наноленты, деформация которого составила 80 % от начальной длины. Указаны четыре области локальных напряже- ний. Максимальный рост напряжения, который составил 32 %, наблюдался в первой области (центр структуры), из которой высвобождаются атомы. Вторая область включает в себя атомы, образующие только две химические связи со своими ближайшими соседями вследствие высвобождения атомов из первой области. Ее напряжение увеличилось на 7 %. Наибольшее увеличение напряженности (порядка 9 %) наблюдается в местах выпуклости и вогнутости волнообразной наноленты (область 3). По краям структуры напряжение, вызванное сжатием наноленты, составило 4 %.

Представленные здесь подходы к оценке распределения напряжений позволяют предположить, что метод анализа карты напряжений является очень перспективным для прогнозирования областей возникновения дефектов вакансии в структуре графеновой наноленты.