Исследование распространения частотно-модулированного излучения в ионосфере с учетом отклоняющего поглощения и влияния внешнего магнитного поля

Настоящая работа посвящена моделирова- нию распространения линейно-частотно-моду-лированного (ЛЧМ) сигнала в ионосферной анизотропной плазме и анализу его ослабления за счет расходимости и отклоняющего поглощения.

ВЕСТНИК 2017

Актуальность данной работы определена широким использованием электромагнитных волн де-каметрового диапазона для обеспечения дальней радиосвязи, радионавигации, радиолокации, загоризонтного радиозондирования, для изучения структуры ионосферы – верхней атмосферы Земли. Несмотря на значительный объем исследований в данной области (см., например, [1–7]), распространение частотно-модулированных (ЧМ) сигналов в ионосферной плазме с учетом магнитного поля Земли изучено еще недостаточно.

В работах [8–13] нами рассмотрено распространение частотно-модулированного излучения в ионосферной плазме, когда источник излучения расположен на поверхности Земли. Распространение ЧМ сигналов в случае изотропной ионосферной плазмы в зависимости от высоты источника излучения рассмотрено в работе [12]. В данной работе особое внимание уделено исследованию ослабления радиосигнала за счет отклоняющего поглощения и расходимости на примере моделей электронной концентрации и частоты соударений электронов для высокоширотной ночной и дневной ионосферы.

1. Математическая постановка задачи

Хорошо известно [14], что эффективная диэлектрическая проницаемость среды для неоднородной анизотропной ионосферы имеет вид

(формула Эпплтона):

E = 1 - V 1 - i Z — -

I u sin2 a 2(1 - v - iZ)

±

----------Y1

—+ u cos a J

24 u sin a

4(1 - v - iZ )

.

и u являются

В выражении (1) параметры v

отношениями квадрата плазменной частоты и квадрата гирочастоты к квадрату рабочей часто- ты, соответственно, то есть: 2

(го ।   4ne N пл v I I 2 ,

V ro )     mero

ГО I _ e ^H 0

u               I 2 2 2 .

^ ro )   me его

( )

В формулах ( ) e = 4,80 9·10^–10 СГСЭ – заряд электрона, m_e = 9,108·10^{– 8} г – масса электрона, с = ,9979 5·10⁸ м/с – скорость света, N – величина электронной концентрации в фиксированной точке пространства. Величина Z – это отношение частоты соударений электронов к круговой рабочей частоте

V

Z = -,                              (3)

ro а величина α – это угол между волновым вектором и напряженностью магнитного поля Земли

H 0 = ( H 0 _x , H 0 y , H 0 _z ). Выражение для квадрата косинуса угла α , необходимое для применения формулы (1), имеет вид:

cos² a =

( H о x k x + H о y k y + H о z k z )²

H 0\k\ 2

В формуле (1) знак плюс соответствует обык- новенной волне, а знак минус – необыкновенной волне.

В приведенных ниже расчетах амплитуда магнитного поля предполагается постоянной, а ориентация напряженности магнитного поля относительно локальной системы координат задается двумя углами γ и φ :

H 0 _x = H ₀cos у cos ф , H 0 y = H ₀cos Y sin ф , ^H 0 z = ^H o ^sin Y .

Если частотой соударения электронов можно пренебречь и положить Z = 0, то формула для эффективной диэлектрической проницаемости имеет стандартный вид (см., например, [4; 7; 14; 15]):

Е ± = 1

-

-

2 v (1 - v )

2(1 - v ) - u sin² a ± u ² sin⁴ a + 4 u (1 - v )² cos² a '

В основе примененного в данной работе под- хода лежат лучевые методы, являющиеся традиционными при описании процессов распространения декаметровых радиоволн в различных средах (см. например [4; 15]). При моделировании лучевых траекторий в анизотропной, неоднородной, среде бихарактеристическая система уравнений с гамильтонианом:

Г= kX + кУ + kz - -г Er (Г, k, ro)(7)

имеет вид [4; 13; 15]:

*- dr  5Г  dk   5Г dt   5Г  dro5Г

— = —— , — =-- — , — =-- ,   = , (8)

dT  d k  dT    d r  dr    d ro  drd где r = (x, y, z) - координаты точки наблюдения, k = (kx, ky, kz) - волновой вектор, ω – круговая частота излучения, t – групповое время,

τ – параметр вдоль лучевой траектории,

E _r ( r, k , го ) - действительная часть эффективной диэлектрической проницаемости среды распространения.

Для применения при численном моделировании системы (7)–(8), необходимо представить диэлектрическую проницаемость (1) в виде суммы действительной и мнимой частей:

E = Er + i Ei .

Анализируя выражение (1), находим, что:

^E r = ¹

-

_________ v ( z _E + r E cos Ф е ) _________ ( z _E + г cos ф _Е )² + ( u _E + r _E sin ф _Е )²,

_________ v ⁽ u _E + r _E sin Ф _Е ) _________

( Z e + Г е cos Ф е ) " + ( U e + Г е S™ Ф е ) " ^.

В формулах (10) и (11) введены обозначения:

z E = ¹ -

(1 - v ) u sin² a 2((1 - v )² + Z ²) ’

В данной работе были приняты следующие значения параметров f ₀ = 2,5 МГц, f_д = 3,75 МГц, T_и =3 с, δ = 1 с^–1. При этом максимальная частота равна приблизительно 10 МГц. Распространение электромагнитной волны изначально осуществляется в плоскости ( x , z ).

Рассмотрим две модели высокоширотной ионосферной плазмы: ночную и дневную. Предполагается, что профили электронной концентрации имеют вид, представленный на рис. 1а, 1б:

„    Zu sin² a

U_E — — Z --5---- у ,

^E         2((1 - v )² + Z ²)

1/4             1

Г е — ± ( x E + y E ) , ф = = 2^arctg

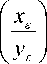
(1 - v ) Zu ² sin⁴ a x_E —                    ,

^E   2((1 - v )² + Z 2 ) 2

У е

— u cos a +

((1 - v )² - Z ²) u ² sin⁴ a 4((1 - v )² + Z ²)²

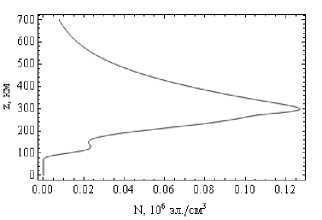
Рис. 1а

Если внешнее магнитное поле отсутствует

( H ₀ = 0), то формула для диэлектрической проницаемости имеет вид [14]:

E — 1 -

v

1 + Z¹

vZ i .

1 + Z²

Предположим, что начальный волновой вектор k (0) параметрически зависит от угла выхода луча α ₀( β ₀ = 0):

k_x (0) — ~ J E T cos a ₀ cos в ₀,

c ky (0) — — Jeccosasnn Д,,              (16)

c

— kz (0) — — VE0 sin a0, c источник излучения точечный, находится вне магнитоактивной плазмы и расположен в точке с координатами (x0, y0, z0):

F| T — 0 = (0 , 0 , 0).                                   (17)

Величина ε ₀ в выражениях (16) – это значение эффективной диэлектрической проницаемо-

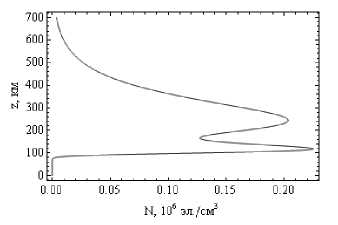
Рис. 1б

Зависимость электронной концентрации от высоты. Рис. 1а – ночная ионосфера, рис. 1б – дневная ионосфера

ВЕСТНИК 2017

сти среды в источнике излучения.

Предположим, что сигнал линейно-частотно-модулированный (ЛЧМ), то есть формула для мгновенной частоты заполнения имеет вид [8; 10]:

Профиль электронной концентрации ночной ионосферы достаточно типичен, слой E слабо просматривается, максимум слоя F значительно меньше, чем в случае дневной ионосферы. Напротив, профиль дневной ионосферы нетипичен, поскольку в максимуме слоя E электронная концентрация больше, чем в слое F.

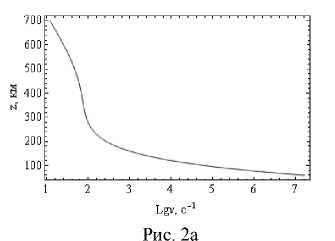
На рис. 2 приведены зависимости электронной частоты соударений от высоты для ночной и дневной ионосферы.

— (0) — — 0 (1 + Sn ), t (0) = n , f ( t ) — f , ( 1 + S t ) , s = 2fgL , f ₀ T_и

где n — начальное время выхода луча, f0 = ω0/(2π) – начальная частота (Гц), fд – девиация частоты (Гц), Tи – длительность импульса (с).

ВЕСТНИК 2017

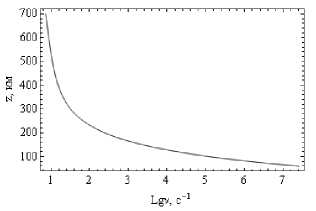
Рис. 2б

Зависимость электронной частоты соударений от высоты. Рис. 2а – ночная ионосфера, рис. 2б – дневная ионосфера

На небольших высотах эти профили практически совпадают. Существенные отличия начинаются выше 110 км, где роль электронной частоты соударений в поглощении (а тем более в отклонении траектории) невелика.

Представленные на рис. 1 и 2 профили коррелируют с данными, приведенными в [16] (80° с.ш., 30° в.д., март).

• 2.    Численное моделирование

• 2.1.    Ночная ионосфера

При вычислении применялись следующие значения параметров: Н ₀ = 0,551 Э, ζ = 0, γ = –83°, φ = 45°. Рассмотрим последовательно результаты численного моделирования в случае ночной и дневной ионосферы.

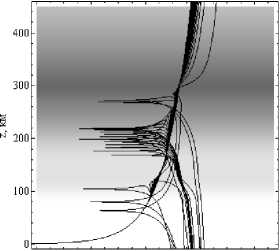
На рисунках 3а и 3б показана лучевая структура ЛЧМ радиосигнала в плоскости (x, z), когда источник излучения находится на Земле. Угол выхода лучей 45°. На рисунках в виде фона показана электронная концентрация ионосферы. В районе 115 км по высоте просматривается слой Е. На высоте порядка 290 км хорошо виден слой F2. Сначала все лучи идут по общей траектории. В диспергирующей среде (ионосфере) они расходятся. Низкочастотные лучи отражаются от слоев Е и F2 и возвращаются на Землю, а высокочастотные просачиваются сквозь слой, при- чем с увеличением частоты траектории выпрямляются.

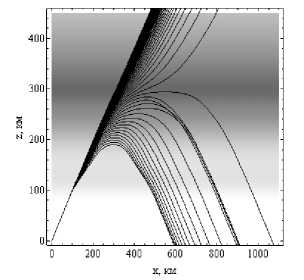
Рис. 3а

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ). Рис. 3а – обыкновенная волна, рис. 3б – необыкновенная волна.

Угол выхода 45°. Ночная ионосфера

Рис. 3б

Лучевые структуры обыкновенной и необыкновенной волн отличаются незначительно, однако для необыкновенной волны просачивание сквозь ионосферу наступает при более высоких частотах, чем для обыкновенной.

На рисунках 4а и 4б показана лучевая структура ЛЧМ радиосигнала в плоскости ( y , z ).

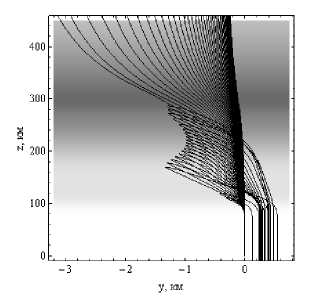
Лучевые структуры ЛЧМ радиосигнала в плоскости ( y , z ). Рис. 4а – обыкновенная волна, рис. 4б – необыкновенная волна.

Угол выхода 45°. Ночная ионосфера

Рис. 4б

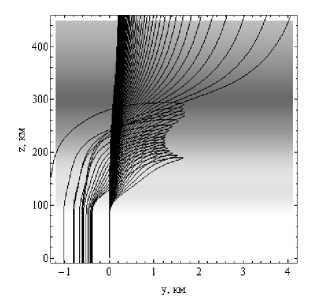
Рис. 4а

Лучи, проходящие ионосферный слой F2 выше 400 км, развертываются параллельно оси z и уходят вверх (высокие частоты). Отраженные лучи (низкие частоты) возвращаются на Землю по близким траекториям, так как горизонтальные градиенты (в рамках модели) отсутствуют. Следует отметить, что лучевая структура необыкновенной волны в этой плоскости выглядит компактнее, чем структура обыкновенной волны, и является как бы ее зеркальным отражением относительно вертикальной оси.

На рисунках 5а и 5б показана лучевая структура ЛЧМ радиосигнала в плоскости ( x , y ). Это вид на лучевую структуру сверху.

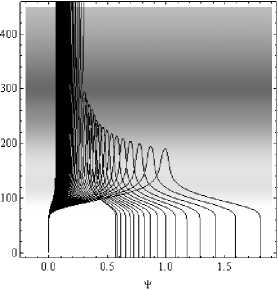
Следует отметить, что при малых значениях отношения эффективной частоты соударения электронов к круговой рабочей частоте ( Z <<1) мнимая часть эффективной диэлектрической проницаемости пропорциональна произведению частоты соударений на квадрат электронной концентрации: ε _i ~ vZ ~ N ² ν _e . С уменьшением высоты ниже слоя E электронная концентрация падает, а частота соударений растет (см. рис. 1, 2), поэтому наибольшее поглощение происходит вблизи нижней границы ионосферы, что и видно на рис. 6 и 7. На рис. 6а и 6б приведены зависимости от высоты поглощения Ψ (в Неперах) вдоль траекторий.

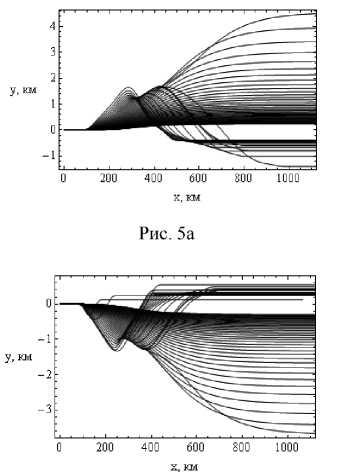
Рис. 5б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , y ).

Рис. 5а – обыкновенная волна, рис. 5б – необыкновенная волна. Угол выхода 45°. Ночная ионосфера

Структура необыкновенной волны в этой

плоскости похожа на «зеркальное отражение» от горизонтальной оси структуры обыкновенной волны. В случае необыкновенной волны рас-

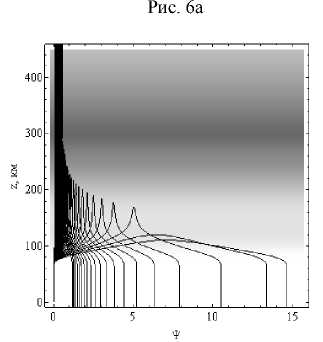
Рис. 6б Зависимости поглощения Ψ (в Неперах) вдоль траекторий от высоты.

Рис. 6а – обыкновенная волна, рис. 6б – необыкновенная волна. Угол выхода 45°. Ночная ионосфера

ВЕСТНИК 2017

пространение сигнала вдоль оси у существенно

«компактнее». В этой проекции хорошо видна каустическая структура и ее особенность – катастрофа A3. Структура волнового поля в окрестности каустического острия (катастрофы A3) подробно исследовалась в работах [17–20].

Рассмотрим теперь поглощение вдоль траек-

торий. Для вычисления поглощения, связанного

с частотой соударения электронов, справедлива

формула:

dΨ dτ

ω ² =- 2 ε i_c 2 .

На рис. 6 можно выделить две группы кривых. Для более высоких частот, проходящих ионосферу, поглощение малó. Более низкие частоты отражаются от слоя. Характерный максимум на кривых – это точка отражения. Эти лучи много времени проводят в нижней ионосфере и испытывают активное поглощение. Естественно с уменьшением частоты поглощение растет,

причем, сопоставляя рис. 6а и 6б, видим, что необыкновенная волна поглощается сильнее обыкновенной.

На рисунках 7а и 7б показано локальное поглощение вдоль лучевых траекторий.

ВЕСТНИК 2017

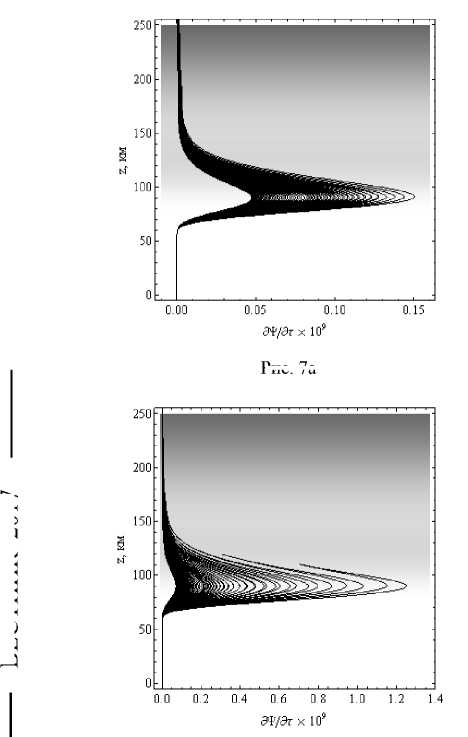
Рис. 7а

Рис. 7б

Зависимости локального поглощения вдоль лучевых траекторий от высоты. Рис. 7а – обыкновенная волна, рис. 7б – необыкновенная волна.

Угол выхода 45°. Ночная ионосфера

Графики на рис. 7 строились в соответствии с формулой (19). На рисунках хорошо видно, как растет поглощение с уменьшением частоты и что на поглощение влияет небольшая область вдоль нижней границы ионосферы. Если иметь в виду, что ниже 65 км обычно в общепринятых моделях данные о частоте соударений и электронной концентрации не приводятся, то понятно, что эта область изучена недостаточно. Графики для мнимой части эффективной диэлектрической проницаемости мы не приводим, поскольку в силу (19) они аналогичны рис. 7.

На рисунках 8а и 8б показаны зависимости от высоты действительной части эффективной диэлектрической проницаемости среды вдоль лучевых траекторий.

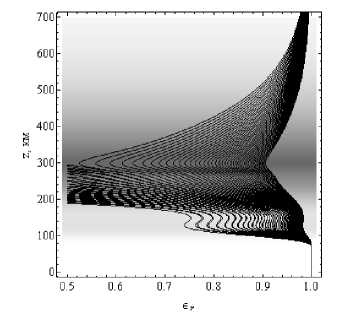
Рис. 8а

Зависимости действительной части эффективной диэлектрической проницаемости среды вдоль лучевых траекторий от высоты. Рис. 8а – обыкновенная волна, рис. 8б – необыкновенная волна.

Угол выхода 45°. Ночная ионосфера

Рис. 8б

Правая часть рисунков ограничена значением 1 (диэлектрическая проницаемость в пустоте), а левая – значением 0,5, что определяется углом выхода лучей α ₀. Поскольку эффективная диэлектрическая проницаемость зависит от координат, а также волнового вектора и частоты сигнала, для каждого луча получается своя зависимость от высоты. Минимумы соответствуют слоям E и F. Рисунки для обыкновенной и необыкновенной волн очень похожи. Следует отметить, что, как следует из расчетов, учет эффективной частоты соударений существенно не влияет на траекторию луча. Это понятно, если учесть, что поправка к ε_r пропорциональна vZ ²~ N ² ν _e ². ^r

На рисунках 9а и 9б показаны зависимости расходимости вдоль лучевых траекторий от высоты в дБ.

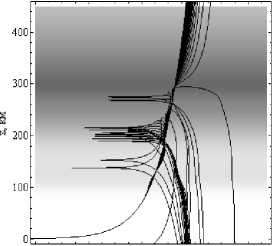
60        80        100       120       140

^к Х а₀ ( П ) = - ^а V^ sin « 0 cos ^Р 0 ,

^к ‘ р ₀ ( п ) = ^{- аЕ} cos « о sin ^р 0 ,

^к' у а ₀ ⁽ П ) = - О С ^Es sin « 0 sin Р о , ^к У Р ₀ ( п ) = ^Д ^ cos « 0 cos ^р 0 ,

^к'га₀⁽ П ) = а7 ДТ cos « 0 , ^кв ⁽ П ) = ⁰ ,

Рис. 9а

60         80         100        120        140

А, дБ

r ‘ ( п ) = 0, г р ₀( п ) = 0, (22) то есть решить расширенную бихарактеристиче-скую систему [4; 21; 22].

Получив решение бихарактеристической системы (21), можно вычислить якобиан J расходимости лучевой трубки:

Рис. 9б

Зависимости расходимости вдоль лучевых траекторий от высоты в дБ.

Рис. 9а – обыкновенная волна, рис. 9б – необыкновенная волна. Угол выхода 45°. Ночная ионосфера.

д x д«0 д x дв^ T1 J = д y дy T2 д«0 дв0 д z д z — — T3 д«0 дР0 — T = f 2 c2 к да1 — 1 /дад           (23) / дк да и найти расходимость поля в каждой точке про-

Для определения расходимости необходимо преобразовать бихарактеристическую систему (8) к виду

dk даД / даД

странства:

A = 10 • lg m         J (r)

dt dr dt

д r

2 c2 к -

д а ’

да 2E1 / да Д д к ) д а ’

известному как бихарактеристическая система Лукина [21; 22], и дополнить ее системой уравнений:

—

^dk « ₀ _ д

^ да1 E

dt

d—

« 0

да

д r

,

д

dt да

— да Д 1 /да 2е

2 c к --— I

дк J/ да

,

—— dk р0

dt

^— dr e o

д дво д

f да Д

д r

,

dt    др ₀

2 — даД | /да2е

2 c к -   — I

д к ] д а

с начальными данными

В формуле (24) J ₀ – якобиан расходимости на условном расстоянии от источника (в расчетах был условно выбран 1 м). Величина ε = ε_r .

На рис. 9 в первую очередь следует отметить тёмную траекторию, соответствующую высокочастотному сигналу. Она имеет небольшой излом в окрестности максимума слоя F, что связано с дефокусировкой сигнала. Горизонтальные линии соответствуют каустикам. Это области усиления поля (фокусировки). Из рис. 9 следует, что лучи, соответствующие дальнему распространению (см. рис. 3), иногда называемые лучами Педерсена, испытывают очень большую расходимость.

С помощью рис. 3, 6 и 9 можно оценить амплитуду сигнала в точке приема. Как известно, действующая напряженность электрического поля изотропного излучателя в пустоте определяется формулой:

30 W

^E д 0 =------ r

В/м,

ВЕСТНИК 2017

где W – мощность в ваттах, а r – расстояние до источника излучения в метрах. Тогда действую- щую напряженность электрического поля в некоторой точке пространства можно оценить по формуле:

E _∂ = E _{∂ 0} e ^{- ψ} 10 ^{- Am /20}В/м. (26)

Например, для ночной ионосферы с частотой ~4 МГц на Земле (расстояние 800 км от источника) поглощение будет порядка одного Непера, а расходимость – около 120 дБ. Если предположить, что мощность источника 1 кВт, то напряженность поля в этой точке составит 64 мкВ/м.

• 2.2.    Дневная ионосфера

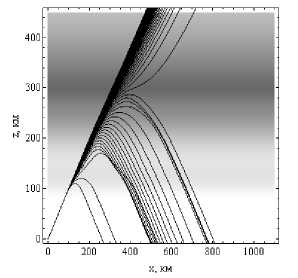
Рассмотрим теперь аналогичные графики для дневной ионосферы. На рисунках 10а и 10б показана лучевая структура ЛЧМ радиосигнала в плоскости ( x , z ).

ВЕСТНИК 2017

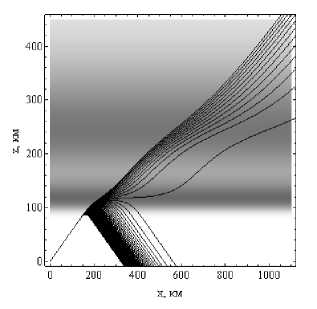
Рис. 10а

Рис. 11а

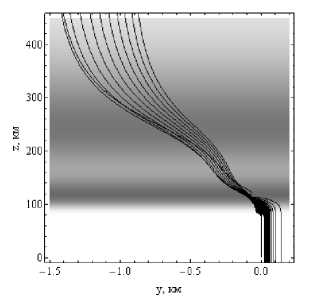
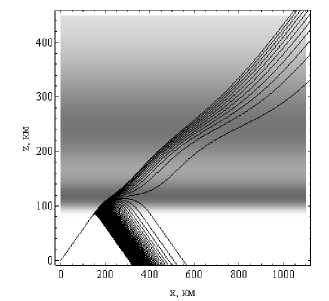
Рис. 10б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ).

Рис. 10а – обыкновенная волна, рис. 10б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

Поскольку в данном случае максимум слоя E больше максимума слоя F, что является аномалией, лучи отражаются только от слоя E (сравните с рис. 3). Если сравнивать с лучевой структурой ночной ионосферы, то дальность связи на одной и той же частоте при фиксированном угле выхода луча заметно уменьшилась (более чем вдвое) и структура стала более упорядоченной.

На рисунках 11а и 11б показана лучевая структура ЛЧМ радиосигнала в боковой плоскости ( y , z ).

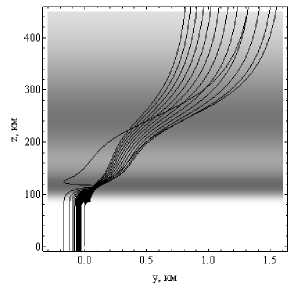
Рис. 11б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( y , z ).

Рис. 11а – обыкновенная волна, рис. 11б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

Главным отличием дневной ионосферы от ночной ионосферы (см. рис. 4) является то, что лучи слабее отклоняются от первоначальной плоскости распространения.

На рисунках 12а и 12б показан вид «сверху» на лучевую структуру, то есть лучевая структура ЛЧМ радиосигнала в плоскости ( x , y ).

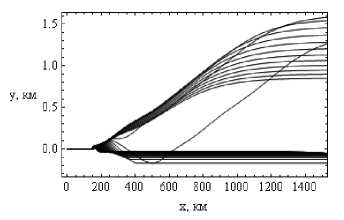
Рис. 12а

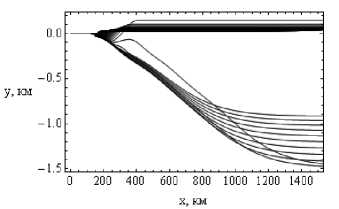
Рис. 12б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , y ).

Рис. 12а – обыкновенная волна, рис. 12б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

Если сравнивать траектории в этой плоскости для дневной и ночной ионосферы (см. рис. 5), то опять-таки видим, что отраженные лучи слабее отклоняются от первоначальной плоскости распространения, что согласуется с рис. 11.

На рисунках 13а и 13б приведены зависимости от высоты поглощения Ψ вдоль траекторий.

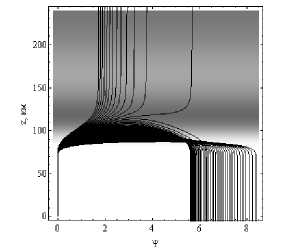
Рис. 13а

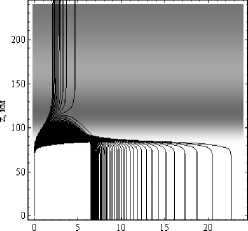
Рис. 13б

Зависимости поглощения Ψ (в Неперах) от высоты вдоль траекторий.

Рис. 13а – обыкновенная волна, рис. 13б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

Сравнивая поглощение в дневной и ночной ионосфере (рис. 6), видим, что оно существенно возросло. Максимальное поглощение для обыкновенной волны – приблизительно 8,5 Нп, а для необыкновенной волны ~ 22,5 Нп. Для частоты ~ 4 МГц поглощение ~ 7 Нп для обыкновенной волны и ~ 10 Нп – для необыкновенной волны.

На рисунках 14а и 14б представлено локальное поглощение вдоль лучевых траекторий.

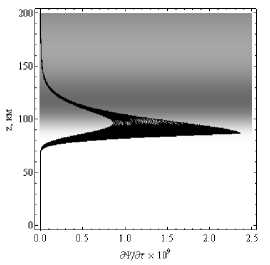
Рис. 14а

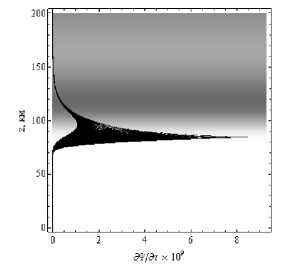
Рис. 14б

Зависимости локального поглощения вдоль лучевых траекторий от высоты. Рис. 14а – обыкновенная волна, рис. 14б – необыкновенная волна.

Угол выхода 30°. Дневная ионосфера

Если сравнивать ночную (рис. 7) и дневную ионосферу, то видно, что пики стали у́ же и значительно длиннее. Они по-прежнему располагаются вблизи нижней границы ионосферы.

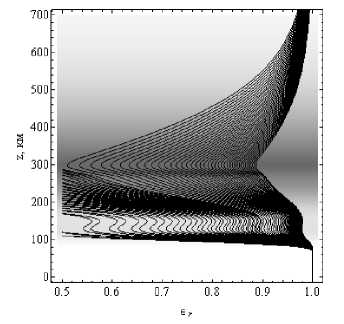
На рисунках 15а и 15б показаны зависимости от высоты действительной части эффективной диэлектрической проницаемости среды вдоль лучевых траекторий.

ВЕСТНИК 2017

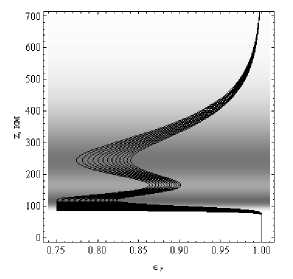
Рис. 15а

ВЕСТНИК 2017

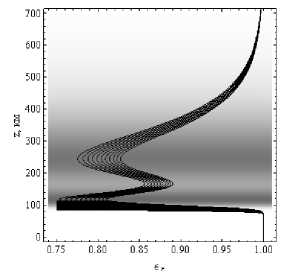
Рис. 15б

Зависимости действительной части эффективной диэлектрической проницаемости среды вдоль лучевых траекторий от высоты.

Рис. 15а – обыкновенная волна, рис. 15б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

По сравнению с рис. 8, характер кривых существенно изменился. Кривые стали компактнее. Это не удивительно, так как поведение кривых отслеживает поведение электронной концентрации (ср. рис. 1а и 1б).

На рисунках 16а и 16б показаны зависимости расходимости вдоль лучевых траекторий от высоты в дБ.

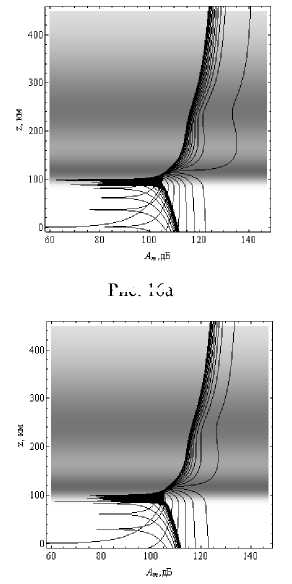
Рис. 16а

Зависимости расходимости вдоль лучевых траекторий от высоты в дБ.

Рис. 16а – обыкновенная волна, рис. 16б – необыкновенная волна. Угол выхода 30°. Дневная ионосфера

Рис. 16б

Как и в случае ночной ионосферы, с помощью рис. 10, 13 и 16 можно оценить амплитуду сигнала в точке приема. Для лучей с частотой ~4 МГц на Земле (расстояние ~350 км от источника) поглощение будет порядка одного 7 Нп для обыкновенной волны и 10 Нп – для необыкновенной волны, а расходимость – около 115 или 110 дБ соответственно. Если предположить, что мощность источника 1 кВт, то напряженность поля в этой точке составит 0,28 мкВ/м для обыкновенной волны и 0,025 мкВ/м – для необыкновенной волны.

Заключение

Таким образом, в настоящей работе выполнено математическое моделирование распространения радиоволн в ионосфере с учетом магнитного поля Земли, частотной модуляции и влияния частоты соударений электронов на отклоняющее поглощение. Сопоставлены особенности распространения ЛЧМ сигналов в двухслоевой анизотропной ионосфере в случае обыкновенной и необыкновенной волн. Исследованы поглощение радиоволны и расходимость вдоль лучей и влияние этих факторов на ослабление амплитуды радиосигнала. Расчеты выполнены для дневной и ночной моделей электронной концентрации высокоширотной ионосферной плазмы. Рассмотрены проекции лучей на разные координатные плоскости: на плоскость распространения, боковую плоскость и «вид сверху». Для расчетов лучевых характеристик применялась бихарактеристическая система дифференциальных уравнений, неизвестными в которой являются координаты луча, компоненты волнового вектора, а также частота и время. Для определения ослабления напряженности электрического поля вдоль траектории рассчитывалась расходимость лучевого потока на основе расширенной бихарактеристической системы уравнений.

Из результатов моделирования следует, что при изучении распространения ЛЧМ сигналов в анизотропных средах необходимо рассчитывать электромагнитные поля со сложной каустической структурой, используя волновую теорию катастроф [15; 23–25], поскольку для описания волновых полей в соответствии с приведенными выше рисунками необходимо рассчитывать поля на каустиках (огибающих лучевых семейств), включая каустические особенности (катастрофы).