Исследование распространения частотно-модулированных пространственно-временных сигналов в неоднородной анизотропной ионосфере

довании процессов распространения коротких

ВЕСТНИК 2013 № 4

волн в различных средах.

Известно, что при моделировании лучевых траекторий гамильтонову бихарактеристиче-скую систему уравнени2 й с гамильтонианом

Γ= k x ² + k y ² + k z ² - ^ω c ₂ ε                     (1)

в неоднородной, анизотропной и нестационарной среде можно представить в виде [1]:

• d r дГ d £_ Sr

T"дк’ dT" "r ’

dt _=-∂Γ d ω ₌ ∂Γ d τ    ∂ ω , d τ ∂ t ,

где k = (kx,ky,kz) – волновой вектор, τ – параметр вдоль лучевой траектории, t – групповое время, r = (x, y, z) - координаты точки наблюдения, ю - круговая частота излучения, е (r, к, ю) -эффективная диэлектрическая проницаемость среды распространения, с = 2,997925 1010 см/с – скорость света. Система (2) обобщает бихарак- теристическую систему, использованную нами в [2] для математического моделирования.

Буквами v и u обозначим, соответственно, отношения квадратов плазменной частоты и гирочастоты к квадрату рабочей частоты:

ωp  4πe2N v=2=      2,

ω ²    m_e ω ²

ω H ²     e ² H 0 ²

u = ₂ = ₂₂₂ ^, ω ² m_e ² c ² ω ²

2. Распространение обыкновенной волны

Рассмотрим распространение частотно-модулированного радиосигнала в неоднородной, анизотропной среде с учетом влияния магнитного поля Земли. Предположим, что изначально

ВЕСТНИК 2013 № 4

где e = 4,8029 10^–10 СГСЭ – заряд электрона, m_e = 9,108 10^–28 г – масса электрона, Н ₀ – величина напряженности магнитного поля Земли, N – профиль электронной концентрации, угол α – угол между вектором напряженности магнитного поля Земли H ₀ = ( H _{0 x} , H _{0 y} , H _{0 z} ) и волновым вектором.

Очевидно, что выражение для квадрата косинуса угла α имеет вид:

cos² a =

H 0 x k + H 0 y k y + H 0 z k z

-12

^H 0 ^{2 k}

.

В качестве модели эффективной диэлектрической проницаемости среды рассмотрим модель неоднородной анизотропной ионосферы

[3]:

ε _± = 1 -

2 v (1 - v )

2(1 - v ) - u sin² α ± u ²sin⁴ α + 4 u (1 - v )²cos² α

где знак «+» соответствует обыкновенной волне, а знак «–» – необыкновенной волне. Предполагается, что источник излучения точечный и расположен в точке с координатами:

^r t = 0 = ( x 0 , У 0 , ^z 0 ) ,             _                     ⁽⁶⁾

а начальный волновой вектор k (0) параметрически зависит от углов выхода луча:

kx (0) = ω ε0 cosζcosη, c ky (0) = ω ε0 sinζcosη,                 (7)

c

ω kz (0) =    ε0 sinη,

c где ε0 – значение эффективной диэлектрической проницаемости среды в источнике. В дальнейшем предполагается, что источник излучения находится вне магнитоактивной плазмы. Кроме того, предполагается, что сигнал линейно частотно-модулированный (ЛЧМ), то есть:

ω (0) = ω 0 (1 + δτ 0 ), t (0) = τ 0 .               (8)

В приведенных ниже расчетах амплитуда магнитного поля предполагается постоянной, а ориентация напряженности магнитного поля относительно локальной системы координат задается двумя углами γ и φ :

H _{0 x} = H ₀cos γ cos ϕ ,

H _{0 y} = H ₀ cos γ sin ϕ ,                     (8)

H _{0 z} = H ₀sin γ .

распространение осуществляется в плоскости

( x , z ). Источник излучения расположен в начале

координат ( x ₀ = y ₀ = z ₀ = 0). Рассмотрим модель двухслойной ионосферной плазмы, для которой профиль электронной концентрации имеет вид

[3–5]:

N ( ? ) = N о

exp2

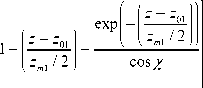
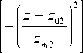
где N ₀ – электронная концентрация в максимуме основного слоя F 2, z ₀₁ – высота максимума слоя F 2, z_{m 1} – условная полутолщина слоя F 2, β – безразмерный коэффициент, характеризующий степень ионизации нижнего слоя по отношению к основному, z ₀₂ – высота максимума нижнего слоя E , z_{m 2} – условная полутолщина нижнего слоя E . Последний член описывает локальные неоднородности ионосферной плазмы.

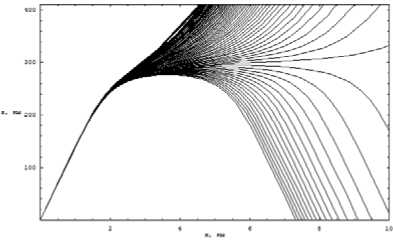
Рис. 1а.

Лучевая структура в плоскости ( x , z ). Обыкновенная волна

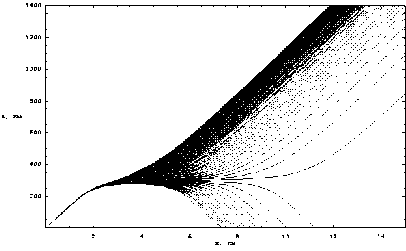
Рис. 1б.

На рис. 1а и 1б в разных масштабах показана лучевая структура ЛЧМ радиосигнала в случае распространения обыкновенной волны в плоскости ( x , z ) при β = 0,1. При вычислении применя-

лись следующие значения перечисленных выше параметров: N ₀ = 2 10⁶ см^–3, Н ₀ = 0,36 Э, z_{m 1} = = 140 км, z ₀₁ = 300 км, z_{m 2} = 40 км, z ₀₂ = 100 км, ζ = 0, η = 89,6º, f ₀ = ω₀ /(2π) = 12,5 МГц, δ =1, γ = 3π/4, φ = π/2, 0 ≤ τ₀ ≤ 90 мс.

На этой частоте часть лучей просачивается сквозь ионосферную плазму, а остальные возвращаются на Землю. Сначала все частоты идут по одной траектории, но, попадая в плазменный слой, их пути разделяются: высокие частоты просачиваются, а низкие частоты возвращаются на Землю. Формально правее мертвой зоны всюду на Земле может быть принят сигнал, однако, за исключением небольшой области, близкой к границе, интенсивность его (в силу расходимости) ничтожна (см. рис. 1б).

Следует отметить, что угол наклона траектории на начальном отрезке и угол наклона предельного луча после выхода из слоя совпадают, поскольку на этих участках волна распространяется со скоростью света. Процесс перехода в прямую линию при τ ₀ → ∞ довольно сложен.

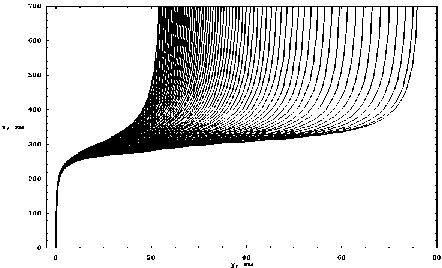
Рис. 2. Лучевая структура в плоскости ( y , z )

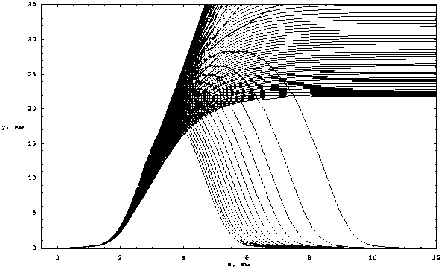
Рис. 3. Лучевая структура в плоскости ( x , y )

На рис. 2 приведены проекции лучевых траекторий в плоскости (y, z). При отсутствии магнитного поля все проекции лучей соответствовали бы линии y = 0. Лучи, возвращающиеся на Землю после отражения от слоя, на этом ри- сунке не видны, так как идут назад по первона- чальным траекториям, поскольку горизонталь- ные градиенты в данных расчетах отсутствуют. Проходящие же лучи ионосфера «сдвигает» в положительном направлении оси y. При этом наибольшие сдвиги у меньших частот, соответствующих так называемым лучам Педерсена. В принципе, можно подобрать такую частоту, для которой сдвиг будет любой наперед заданной величиной. Другое дело, что в силу расходимости лучевого потока интенсивность поля, образованного такими лучами, будет ничтожна.

На рис. 3 показана проекция лучевой структуры на Землю, то есть распространение лучей в плоскости ( x , y ). Здесь уже хорошо видны лучи, отраженные от ионосферы и вернувшиеся на Землю, а также семейство лучей, прошедших ионосферный слой и распространяющихся вдоль оси x .

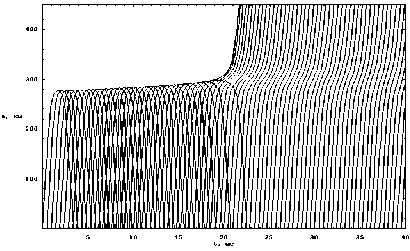
Рис. 4. Лучевая структура в плоскости ( t , z )

На рис. 4 представлено распространение обыкновенной волны в плоскости ( t , z ). Видно, что семейство пространственно-временных лучей, отражающихся от ионосферы и имеющих огибающую, образует пространственновременную каустику с краем (краевая катастрофа B₃) (подробнее см. в [6–10], а также работу [11] и ссылки в ней). Необходимо отметить, что для наглядности при расчете было взято в два раза больше лучей, чем на всех других рисунках.

ВЕСТНИК 2013 № 4

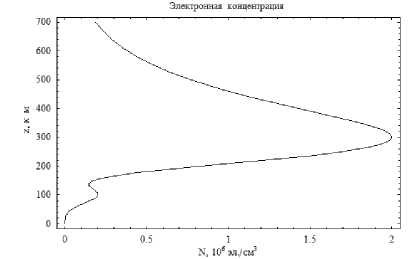
Рис. 5. Профиль электронной концентрации

На рис. 1–4 влияние второго слоя (слоя Е , см. рис. 5) в силу достаточно высокой начальной частоты ничтожно. Однако если понизить начальную частоту, то лучевая структура существенно дополнится. На рис. 6, соответствующем плоскости ( x , z ), видно, что с ростом частоты лучи сначала отражаются от слоя Е , потом идет (по углам) переходная область. При этом лучи, отраженные от слоя Е , засвечивают на Земле всю область справа, но с минимальной интенсивностью, а далее формируется структура, обсуждавшаяся выше.

ВЕСТНИК 2013 № 4

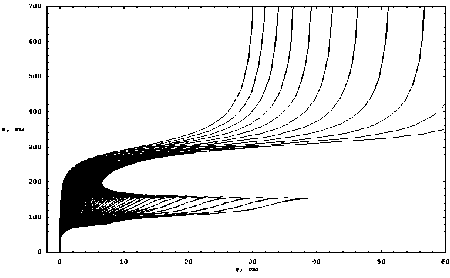
Рис. 7. Лучевая структура в плоскости ( y , z )

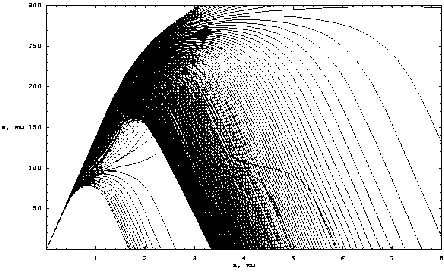
Рис. 6. Лучевая структура в плоскости ( x , z )

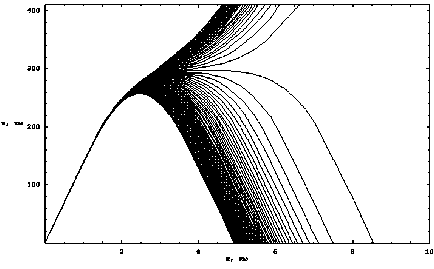
Рис. 8. Лучевая структура в плоскости ( x , z ) Необыкновенная волна

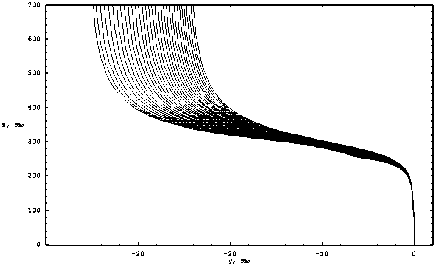
Рис. 9. Лучевая структура в плоскости ( y , z ) Необыкновенная волна

Сопоставим полученные результаты. Сравнивая рис. 1а и 8, описывающие лучевое распространение в плоскости ( x, z ), видим, что число лучей, прошедших ионосферный слой, существенно уменьшилось. Ширина мертвой зоны (куда не приходят ионосферные лучи) также уменьшилась с 7,3 км до 5 км. Более компактно выглядит боковое отклонение лучей (сравните рис. 2 и рис. 9). Причем если в случае обыкновенной волны прошедшие ионосферу лучи параллельно сдвигаются вправо по оси y , то в случае необыкновенной волны они сдвигаются влево.

На рис. 7 показана лучевая структура в плоскости ( y , z ). Следует обратить внимание на характерный «выброс вправо», описывающий выход из основной плоскости распространения лучей в результате взаимодействия со слоем Е . При расчетах предполагалось, что β = 0,1; f ₀ = ω₀ /(2π) = 3,5 МГц; 0 ≤ τ₀ ≤ 2790 мс.

3. Распространение необыкновенной волны

При построении лучевой структуры необыкновенной волны использованы те же параметры, что и в первой части статьи (до уменьшения начальной частоты сигнала).

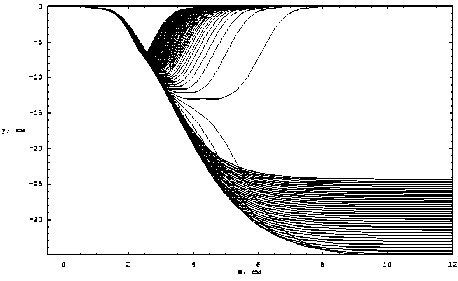
Рис. 10. Лучевая структура в плоскости ( x , y ) Необыкновенная волна

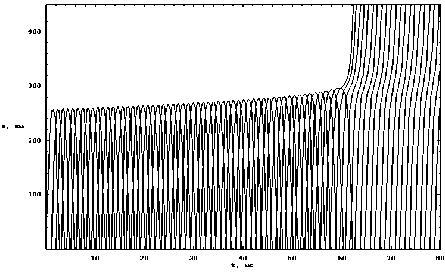
Рис. 11. Лучевая структура в плоскости ( t , z ) Необыкновенная волна

Сопоставляя рис. 3 и рис. 10, видим, что лучевая структура, опять-таки став более компактной, как бы зеркально отразилась относительно горизонтальной оси.

На рис. 11 представлено распространение необыкновенной волны в плоскости ( t , z ). При сравнении с рис. 4 видим, что число пространственно-временных лучей, отражающихся от ионосферы и касающихся огибающей (каустики), существенно возросло.

6. Заключение

Таким образом, в работе рассмотрены особенности распространения частотно-модулиро-ванных сигналов в анизотропной ионосферной плазме как в случае обыкновенной, так и в случае необыкновенной электромагнитной волны. Основным инструментом исследования являлась бихарактеристическая система дифференциальных уравнений, неизвестным в которой являются не только координаты и компоненты волнового вектора, но также частота и время. Исследовано распространение декаметровых радиоволн в случае двухслоевой модели ионосферы Земли. Проанализированы особенности выхода как обыкновенной, так и необыкновенной волны из плоскости распространения, а также образование каустики пространственно-временных геометрооптических лучей. Дальнейшие исследования особенностей распространения частотно-модулированных радиоволн в анизотропных средах требуют расчета электромагнитных полей при наличии сложной каустической структуры, что обеспечивает метод канонического оператора Маслова (см. [1; 12; 13]) и волновая теория катастроф [8–11]. Кроме того, для адекватного описания распространения радиоволн в ионосфере Земли целесообразно строить динамические модели [14], используя профили электронной концентрации, восстановленные по данным радиотомографии [15–16].