Исследование рассеивающих свойств нелинейного биконического отражателя - физической модели боеприпаса с электронными устройствами

Впоследнее время внимание специалистов, занимающихся гуманитарным разминированием, борьбой с терроризмом, криминалистикой и другой деятельностью все больше привлекает обнаружение скрытых объектов в различных укрывающих средах. Решение этих задач с использованием линейных радиолокационных методов сопряжено с большими трудностями селекции объектов на фоне сильных отражений от поверхности укрывающей среды (земли, листвы, деревьев, морской поверхности и т. п.). Идея локации объектов искусственного происхождения, обладающих нелинейными свойствами, возникла в 70-х годах прошлого столетия. Данное направление получило название нелинейной радиолокации. Сущность эффекта, используемого в нелинейной радиолокации, заключается в том, что некоторые объекты или их элементы (полупроводниковые радиоэлементы, точечные прижимные металлические контакты) при облучении электромагнитной волной обладают способностью генерировать спектральные составляющие, отсутствующие в спектре падающей электромагнитной волны. Избирательный прием этих составляющих позволяет расширить возможности нелинейных радиолокационных станций в сравнении с обычными станциями, использующими линей- но-отраженный сигнал. Таким образом, удается избавиться от сильных фоновых отражений, которые в ряде случаев делают невозможным использование обычных радиолокационных методов поиска и обнаружения объектов.

Процесс обнаружения объектов, содержащих в своем составе полупроводниковые элементы, в нелинейной радиолокации имеет ряд особенностей. Как правило, для обнаружения таких элементов используются сверхвысокочастотные зондирующие поля на частотах f = 0,3 – 1 ГГц. При этом в процессе формирования гармоник и комбинационных частот рассеянного, например, боеприпасом с электронными устройствами, электромагнитного поля особую роль будут играть p-n -переходы полупроводниковых элементов (транзисторов, диодов).

В известной литературе, в области нелинейной радиолокации отсутствуют публикации, отражающие особенность формирования гармоник и комбинационных частот при использовании многочастотных радиосигналов, а также сигналов на частотах свыше 1 ГГц. Кроме того, в известной литературе в качестве нелинейных отражателей, как правило, рассматриваются резонансные электрические вибраторы, нагруженные на СВЧ-диоды [1 – 4]. Такие физические модели зачастую снижают практическую значимость результатов исследований, т.к. не позволяют выявить особенности преобразования сигнала в широком диапазоне частот.

Целью статьи является исследование возможности обнаружения боеприпасов, включающих электронные компоненты, с использованием в качестве физической модели широкополосного нелинейного биконического отражателя, а так же изучение закономерностей изменения нелинейной эффективной поверхности рассеяния (НЭПР) на частотах падающего поля от 0,5 до 3 ГГц. Выявление степени и характера влияния нелинейных элементов рукотворных объектов на отраженный радиосигнал, обеспечивает возможность прогнозирования величины НЭПР реальных боеприпасов с электронными устройствами (при наличии априорной информации об их элементной базе).

Для исследования величины НЭПР нелинейного элемента использовалась следующая методика:

• 1)    анализ явления и обоснование физической модели нелинейного отражателя;

• 2)    разработка математической модели расчета тока в широкополосной биконической антенне, нагруженной на нелинейный элемент;

• 3)    моделирование процесса рассеяния радиоволн на бико-ническом нелинейном отражателе;

• 4)    анализ результатов моделирования.

Важно установить влияние электрических характеристик точечного элемента – полупроводникового диода на НЭПР всего отражателя. Целесообразно, чтобы основные параметры выбранного отражателя мало изменялись в диапазоне частот анализируемых гармоник и комбинационных частот. Это обеспечит большую ясность при анализе физических процессов формирования вторичного сигнала нелинейным точечным элементом. В известных работах в области нелинейной радиолокации в качестве линейной части отражателя использовался резонансный электрический вибратор. Однако параметры такого вибратора значительно изменяются при изменении длины волны электромагнитного поля,

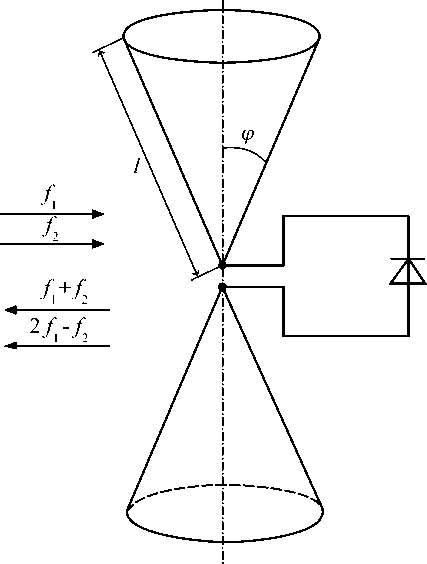
Рис. 1. Биконический вибратор с нелинейным элементом – физическая модель боеприпаса с электронными устройствами что вызывало затруднение при интерпретации результатов исследований. Поэтому предлагается использовать не проволочный вибратор, а биконический (рис. 1). Известно, что основные параметры этого вибратора при больших углах между осью конуса и его образующей практически постоянны в 4-5-кратном диапазоне частот [5, 6]. Известно [6], что при 2πl/λ > 1 входное сопротивление этого вибратора чисто активное и практически постоянно в широком диапазоне длин волн (при ϕ = 30^ и длине образующей, равной 0,1 м, сопротивление биконической антенны в диапазоне частот от 500 МГц до 3 ГГц составит ra ≈ 200 Ом). Кроме того, по своей форме биконический отражатель имеет объемную (трехмерную) структуру, более близкую к реальным объектам поиска, чем проволочный вибратор. Таким образом, использование биконического вибратора (соответствующего размерам реальных объектов поиска) в качестве линейной части нелинейного отражателя позволяет наиболее корректно оценить влияние его нелинейной нагрузки (p-n-пе-рехода полупроводникового прибора) на величину НЭПР в чистом виде. Соответственно физическая модель в виде би-конического отражателя, нагруженного на p-n-переход полупроводникового прибора, наиболее близко соответствует реальному физическому процессу.

В качестве нелинейного элемента рассматривается полупроводниковый диод. Полный ток через p-n -переход диода складывается из диффузионного тока, обусловленного движением носителей заряда вследствие наличия градиента их концентраций, и дрейфового тока, создаваемого движением носителей заряда в электрическом поле.

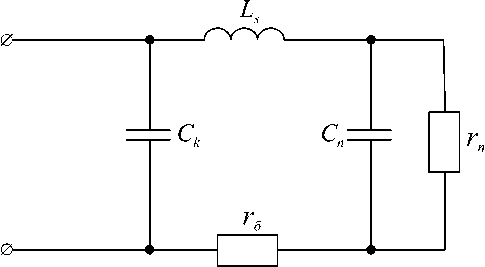
Рис. 2. Эквивалентная схема полупроводникового диода

тивления p-n -перехода. При больших токах дифференциальное сопротивление перехода мало и общее сопротивление определяется сопротивлением базы. При этом зависимость тока от напряжения представляет собой линию, угол наклона которой пропорционален величине r_б .

Величина сопротивления перехода не остается постоянной на разных частотах. Зависимость r_п от частоты для малого сигнала определяется выражением [7]

rn (® ) = ------------/     ,Л( I + IQ )-^1 + .^1 + ^Tp

Таким образом, полный ток через p-n -переход полупроводникового диода можно описать выражением

i (t) = io (e ш -1),

где τ_р – среднее время жизни дырок в n -области.

Емкость С_п при прямом смещении диода состоит из барьерной емкости С_б и диффузионной емкости С_д , обусловленных неосновными носителями в нейтральных областях диода.

Частотная зависимость барьерной емкости проявляется только на частотах, соизмеримых с частотой диэлектрической релаксации материала

где i₀ – обратный ток, определяемый физическими свойствами полупроводникового материала; U – напряжение на полупроводниковом диоде; λ = q/kT – величина, зависящая от температуры p-n -перехода, при комнатной температуре λ^-1=25 мВ, q – величина заряда электрона; T – абсолютная температура.

У реального диода необходимо учитывать также сопротивление базы r_б , емкость корпуса С_к , индуктивность выводов и контактной пружины, соединяющей кристалл с одним из выводов L_s , а также емкость p-n -перехода С_п . В общем случае диод может быть представлен эквивалентной схемой, изображенной на рис. 2 .

Индуктивность L_s составляет 1 - 20 нГн, поэтому ее имеет смысл учитывать на частотах свыше 100 МГц, где сопротивление ωL_s становится соизмеримым с прямым сопротивлением диода. Емкость корпуса С_к современных СВЧ-диодов обычно не превышает 0,1–1 пФ. Сопротивление перехода r_п шунтируется емкостью С_п . В зависимости от величины напряжения, приложенного к диоду, меняются величины r_п и С_п .

Последовательно с p-n -переходом диода меняется сопротивление базы r_б . При больших прямых токах падение напряжения на сопротивлении базы соизмеримо с падением на переходе. С учетом сопротивления базы аналитическое выражение зависимости тока диода от приложенного к нему напряжения может быть представлено в следующем виде

I = I 0 ( e ^я ( U ^- Ir ) - 1 ) . (2)

Проведя логарифмирование и дифференцирование выражения (2), получим дифференциальное сопротивление в любой точке прямой ветви вольтамперной характеристики

f E = 1/2 7L£ o £p .

Так, для германия с удельным сопротивлением 0,1 Ом·см частота f_ε ≈ 10¹² Гц. Поэтому на частотах вплоть до 10¹² Гц зависимостью емкости С_б от частоты можно пренебречь. Величина барьерной емкости зависит от напряжения на переходе и для диодов с резким переходом определяется соотношением [7]

б

ε ε 0 q N2(U + Фк)

—

= A (U + Фк) 2

где А₀ – коэффициент, учитывающий константы и геометрию сплавного перехода; ϕ_к – контактная разность потенциалов. Для диодов с плавным переходом (диффузные диоды) выражение для барьерной емкости имеет вид [7]

ε ε 0 q N12(U + Фк)

—

Ao (U + Фк) 3

где А₀ – коэффициент, учитывающий константы и геометрию диффузного перехода.

Диффузионная емкость диода пропорциональна прямому току и времени жизни τ_р неосновных носителей и определяется соотношением

Cg = 2 (I + Io )Tp X.                                  (8)

Rg =

1Я( I + Io)

^{+ r} 6 .

Величина диффузионной емкости зависит также и от частоты, причем эта зависимость особенно заметна на частотах, соизмеримых с временем жизни неосновных носителей в базе диода [7]

Из формулы (3) следует, что при малых токах дифференциальное сопротивление зависит главным образом от сопро-

Сдиф (Ю) =

XTp (I + Io)

V2 ^i+^1+® 2tJ"

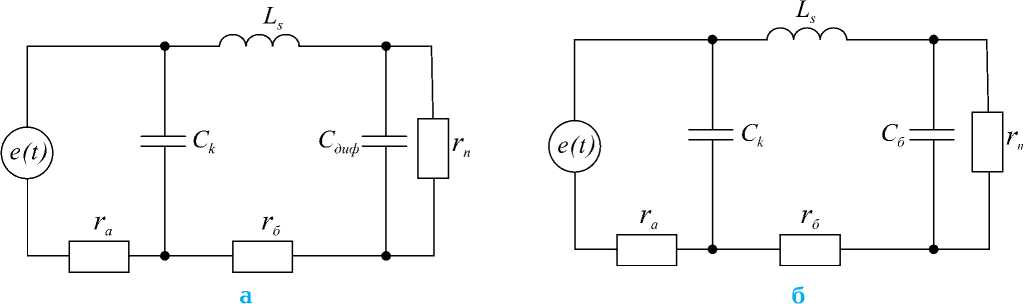
Рис. 3. Эквивалентная схема биконического нелинейного отражателя: а - при прямом включении; б - при обратном включении

Диффузионная емкость даже при небольших прямых токах значительно превосходит барьерную, поэтому при прямом включении диода барьерной емкостью можно пренебречь. При обратном включении диода барьерная емкость значительно превышает диффузную.

Таким образом, основными параметрами диода являются:

• ♦    индуктивность выводов L s ;

• ♦    емкость корпуса С к ;

• ♦    дифференциальное сопротивление, включающее в себя сопротивление перехода, базы, омического контакта и выводов.

При работе диода в прямом направлении необходимо дополнительно учитывать диффузную емкость p-n -перехода С_ди ф , а при обратном включении – барьерную емкость p-n -перехода C_б .

С учетом этого эквивалентная схема биконической антенны, нагруженной на полупроводниковый диод, для прямого и обратного включения примет вид, показанный на рис. 3 .

На эквивалентных схемах, представленных на рис. 3, параметр ra представляет собой сопротивление биконического вибратора, приведенное к точкам включения нелинейного элемента. Данное сопротивление является чисто активным и равно сопротивлению излучения в широком диапазоне частот от λ ≈ πl до λ ≈ πl/(4…5), где l – длина плеча вибратора. Коэффициент направленного действия (КНД) бико-нического вибратора при этом приблизительно равен КНД полуволнового вибратора, т.е. 1,6. Таким образом, основные параметры биконического вибратора практически не изменяются в широком диапазоне частот, следовательно, сопротивление антенны rа можно считать постоянной величиной. Учитывая, что эквивалентная схема различна для случаев прямого и обратного включения диода, в зависимости от приложенного к нему напряжения, то и рассматривать эти случаи следует отдельно. Для определения тока, протекающего через нелинейный элемент, нагруженный на бикони-ческую антенну, производился расчет дифференциального сопротивления электрической цепи полупроводникового диода на основании эквивалентных электрических схем, представленных на рис. 3. Выражения для расчета сопротивления диода с учетом рассмотренных паразитных емкостей и индуктивностей имеют следующий вид для прямого и обратного включения:

R дпр =

R _Е X ( i ( t ) + i₀ ) k₂ + Vk k_;

R _Е Xro C k ( i ( t ) + i₀ ) k₂ + Vk k_{1 to} C_k + X ( i ( t ) + i₀ ) k₂

RRR_TA₍to + RXkk ( i ( t ) + L ) + Rkk __                                         2 О 2     1 3 \ V ' О /          3

д обрRRRyAXto2C + RyXk,k^Ct (i(t) + ifl) + Vkk^Ск + Vk A.to + Xk,k, (i(t) + i„) 2 О        k 2   13k          О          3 k          О         13          О k i = V1+ V1+ ® 2T2 ,

e(0 =

RWa + i_np^R_dnp, при e(0 > 0; RWc H₆p(0R_do6p, при e(t) < 0.

k₂ = k 1 + to t _p ,                                        (13)

k₃ = 2^{e (} t ) ⁺ Ф _k ,                                     ⁽¹⁴⁾

где R_Σ = ωL_s + r_б – суммарное сопротивление базы и индуктивности выводов элемента.

При использовании второго закона Кирхгофа уравнение для электрических цепей ( рис. 3), примет вид (15).

В результате решения уравнений (15) были получены аналитические выражения описывающие амплитуду тока i(t) в биконической антенне

^ =

2 ,npue(t)>0;

io6p e(Z)<0.

i np t t ) =

-r RyXa Cik - V2rko C - r Xki - RyXkAn + e(t)RyXoC + e(t)XL + лDT a ti к 0 2          a 1 к a 2 0 ti 20            ti к              2          np

2 ( rR Хо Ск + r Л К , + R_y X k )

a ti к 2 a 2 ti 2

D „ = (rR = Хю СД о k 2 + V2 r„k₁ ro C_l + r a X k 2 i о + R _I X k 2 i, - e ( t ) R , X_m C_t - e ( t) X k 2 ) +

+ 4 ( rU m C, k , + r , X k , + R , X k, )( KR X C k, i , + R A L ) ,                                     (18)

a ^ k 2 a 2       ^     2 a ^ к 2 о ^     20

i я (t) = обр

- r_a to C_k ( V2 R ₂ A 0 to + R ₂ X k 1 k 3 i ₀ + V2 k 3 ) - r a ^ A 0 ro - X k 1 k 3 i ₀ ( r a + R ^ ) - 2RR ₂ A ₀ ю - V2 k 3 + e ( t ) X k 1 k 3 ( ro C_kR ₂ + 1 )

2 ( r R_y Xro CJ* + r kk X + R_y X kk )

a ^ k 13 a 13      ^   13

+

+

D обр

2 ( r a R _s Xro C_kk 1 k 3 + r_ak 1 k 3 X + R ₂ X k 1 k 3 ) '

D np = ( r a _toC_k ( 72 R ₂ A 0 rn + R ₂ X k 1 k 3 i ₀ + 72 k 3 ) + r a 72 A ₀to - X k 1 k 3 i ₀ ( r a + R _s ) + 72 R ₂ A 0 to + 72 k 3 - e ( t) Xk 1 k 3 ( ® C_kR ₂ + 1 ) ) 2 +

+ 4 e ( t ) ( r R_y Xto C_k k , k , + rk k X + R _y X k _A k , ) ( to C , (72 R , A to + R , X k , kA , + 72 k , ) + 72 A to + X k , kA, ,.        (20)

a ^ к 13 a 13       ^    13 к ^ 0        ^    1 3 0         3          0        1 3 0

Полученные аналитические выражения (16) – (20) описывают ток, протекающий в биконической антенне, нагруженной на полупроводниковый диод. Этот ток будет возбуждать в антенне колебания, которые излучаются ею в пространство. Поскольку форма тока в антенне за счет воздействия нелинейного элемента (полупроводникового диода) будет отличаться от формы возбуждаемых в ней высокочастотных колебаний Е(t) , то это приведет к появлению в переизлучаемом сигнале дополнительных гармонических и комбинационных составляющих.

Для расчета НЭПР нелинейного отражателя используется выражение [8, 9]:

Величина плотности потока мощности СВЧ-поля, падающего на отражатель, определяется выражением [10]:

= ^{π 2 E 2}

П пад = 2 λ 2 ρ ₀

где λ₁ – длина волны первичного поля; ρ₀ – волновое сопротивление свободного пространства.

Таким образом, с учетом (22–24) выражение для расчета НЭПР нелинейного биконического отражателя примет вид:

σ

н

^{ρ 0 D n λ 1 2 r a iг2}

σ _н = 4 π r ² П ^{n p} , П пад

π ² E м ²

.

где r – расстояние до нелинейного отражателя; П_пр – плотность потока мощности в точке приема на частоте исследуемой гармоники; П_пад – плотность потока мощности, падающего на нелинейный отражатель на частоте первичного поля.

Плотность потока мощности П_пр определяется формулой

П n p

PD нn

4 π r ^{2 ,}

где Р_н – мощность, рассеиваемая нелинейным отражателем на гармонике; D_n – коэффициент направленного действия биконического отражателя на гармонике или комбинационной частоте.

В свою очередь мощность, рассеиваемая нелинейным бико-ническим отражателем на гармонике, будет равна

P = U ^г = 0 , 5 i ² r . нa 2r

a

Для оценки величины комбинационных составляющих в переизлученном сигнале использовалось преобразование Фурье, с помощью которого определялись токи i_г дополнительных гармоник, характеризующих НЭПР. По амплитуде полученных в результате преобразования Фурье токов комбинационных гармоник рассчитывалась НЭПР биконичес-кого отражателя.

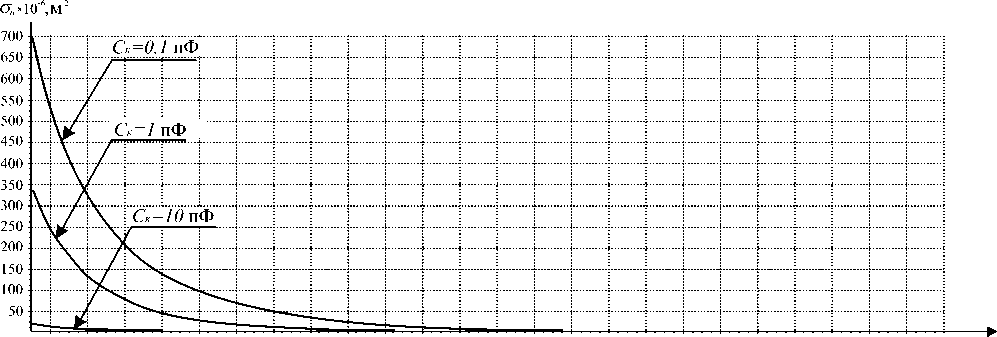
Результаты оценки НЭПР биконического вибратора, нагруженного на полупроводниковый диод (с помощью предложенной математической модели), для гармоник с частотами f₁ + f₂ и 2f₂ - f₁ , представлены на рис. 4, 5 . Для получения данных зависимостей в диапазоне частот от 0,5 до 3 ГГц использовались следующие параметры L_s = 0,01 мкГн, r_a = 200 Ом, r b = 40 Ом, E м = 5,2 В, i 0 = 10^–6 А, λ = 40 В^–1, А 0 = 10^–11 , ρ₀ = 120π Ом, D_n = 1,6 . При этом необходимо отметить, что наводимая на антенне ЭДС E_м = 5,2 В соответствует плотности потока мощности падающей волны 1 Вт/м² для частот f 1 ≈ f 2 ≈ 500 МГц.

Формирование расчетных данных осуществлялось для трех значений входной емкости полупроводникового элемен-

600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 2600 2700 2800 2900 3000/МГц

Рис. 4. НЭПР биконического вибратора на частоте f1 + f2

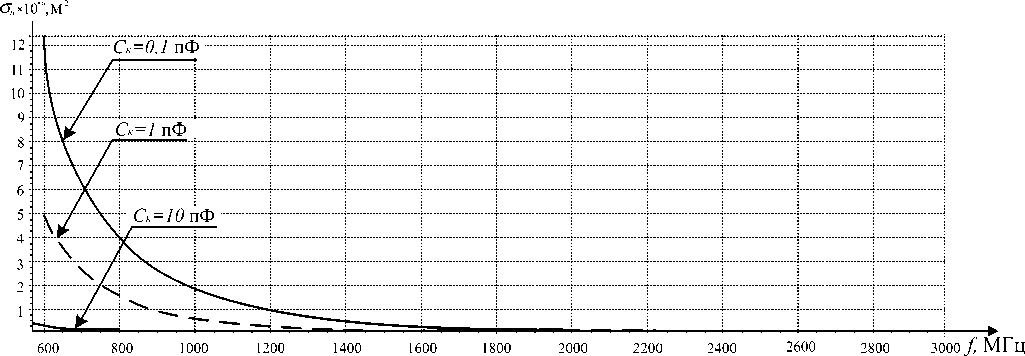
Рис. 5. НЭПР биконического вибратора на частоте 2f2 – f1

та С_к : 10, 1 и 0,1 пФ. Указанные значения С_к соответствуют среднечастотным, высокочастотным и сверхвысокочастотным полупроводниковым элементам.

Анализ зависимостей, представленных на рис. 4, 5 , показывает, что при увеличении частоты зондирующего сигнала происходит закономерное снижение величины НЭПР. Это вызвано закорачивающим влиянием емкости выводов С_к и потерями энергии на индуктивности L_s . Необходимо отметить, что наиболее существенное влияние на величину НЭПР оказывает значение входной емкости, которое не зависит от величины наведенной ЭДС на выводах биконической антенны и линейно шунтирует ток через p-n -переход. Таким образом, из анализа следует, что для искусственных объектов поиска, использующих в своем составе современную элементную базу с малыми С_к , с ростом частоты зондирующего сигнала величина НЭПР снижается менее интенсивно.

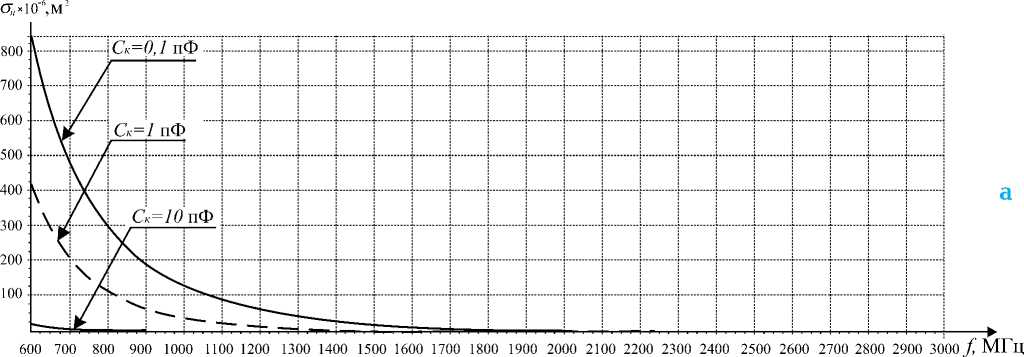
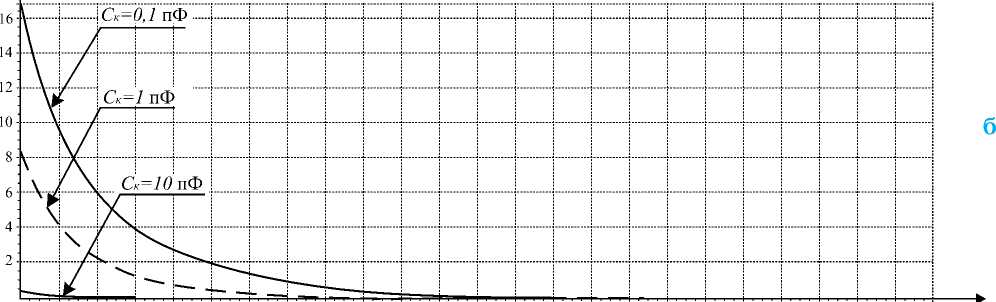
Для сравнения возможностей обнаружения боеприпасов с электронными устройствами с помощью одночастотного и двухчастотного метода нелинейной радиолокации проводилось моделирование отражений от нелинейного биконичес-кого вибратора при облучении его сигналом на одной частоте f1. При этом анализировался уровень нелинейных гармоник с частотами 2f1 и 3f1. Результаты моделирования для одночастотного облучающего сигнала приведены на рис. 6. Сравнение данных, приведенных на рис. 6 и рис. 4, 5 показывает, что величины НЭПР нелинейного биконического отражателя на частоте 2f1 незначительно отличаются от частот f1 + f2 для двухчастотного метода. Однако комбинационная гармоника третьего порядка 3f1 имеет амплитуду существенно меньшую, чем на частоте 2f2 – f1. Это обусловлено тем, что для более высокой частоты 3f1 весьма сильное влияние оказывает закорачивающее воздействие входной емкости полупроводникового элемента.

Таким образом, для поиска объектов, содержащих нелинейные элементы, такие как современные полупроводниковые приборы с малыми значениями входных емкостей, возмож-

600 700 SOO 900 1000 1100 1200 1300 1400 1500 1600 1700 ISOO 1900 2000 2100 2200 2300 2400 2500 2600 2700 2800 2900 3000/МГц

Рис. 6. НЭПР биконического вибратора на частоте 2f1 (а) и 3f1 (б)

но использование зондирующих сигналов на частотах до 2,5 ГГц. При этом при локации целесообразно использовать два и более зондирующих СВЧ-сигналов, а анализ осуществлять на комбинационных составляющих второго и третьего порядка. Это обусловлено значительной большей энергетикой составляющих на частоте 2f2 – f1, по сравнению с час- тотой 3f1 для одночастотного метода локации. Кроме того, обратная волна на комбинационной частоте третьего порядка будет иметь меньший декремент затухания при нахождении боеприпаса в толще грунта, а диаграмма рассеяния меньшие «провалы» в сравнении с одночастотной локацией.