Исследование равновесий в неводных растворах поликислот (модель и эксперимент)

Многоосновные кислоты являются исходными соединениями в синтезе термостойких полимеров. Существующие методы расчета и определения констант диссоциации многоосновных кислот, предложенные Спикменом [1], позднее Бейтсом [2], справедливы для водных растворов. Определение ступенчатых констант диссоциации многоосновных кислот в неводных растворах представляет значительную трудность из-за невозможности прямого определения активности ионов водорода (для простоты рассуждений - концентрации ионов водорода [ H + ]) в каждой точке титрования. Поликислоты обычно характеризуются близостью констант диссоциации. Поэтому число скачков на кривых потенциометрического титрования не соответствует числу функциональных групп многоосновных кислот, что затрудняет непосредственное определение нескольких рК . Отметим, что для раздельного определения констант диссоциации поликислот (или смеси электролитов) необходимо, чтобы отношение ближайших констант диссоциации было не менее 1000.

Представим равновесия в растворах поликислот

H _n A = H (_n - 1) A - + H

H (n - i) A - = H (n — 2) A 2 + H +                                          (1)

HA⁽¹ - ⁿ⁾ = A^n- + H⁺

Константы диссоциации последовательно запишем в виде:

K 1 = [H⁺] ⋅ ([H (n - 1) A] - /[H n A]) ⋅ f 1 /f 0

K2 = [H+]⋅([H(n-2)A]2-/[H(n-1)A]-)⋅f2/f1 ................... (2) Kn = [H+]⋅([A]n-/[HA]1-n)⋅fn/fn-1, где K1,K2,...Kn - термодинамические константы диссоциации поликислоты, [H+] - активность ионов водорода, f0,f1,f2,...fn - коэффициенты активности молекулы HnA и ионов H(n_1)A-,H(n-2)A2-,...An-, n - основность кислоты.

Уравнение (2) позволяет определить константы диссоциации поликислот методом потенциометрического титрования при предварительном экспериментальном установлении стандартного потенциала цепи без переноса

Стеклянный электрод /НС1О 4 / AgCl, Ag    (I)

в соответствующих растворителях, значение которых E ₀ используется для оценки [H + ] в каждой точке титрования поликислоты по уравнению Нернста. Оценка значений коэффициентов активности f i , f ₂ , ..., f _n проводится по известным методам (например, методом Дэвиса).

Стандартный потенциал цепи (I) определен по методике В.В.Александрова с сотр. [3], а также методом параболического приближения функции

E’ = (Е + 2 6 lgm a ) при m a = 0.                               (3)

Математическая обработка результатов эксперимента по компьютерным программам [4.-Приложения II, III] приводит к получению стандартного потенциала Е 0 в среде ДМФ , равного 0.427 B, с коэффициентом корреляции К _кор = 0.9300.

При титровании четырехосновной кислоты, например, этилендиаминотетрауксусной кислоты ( ЭДТА ) раствором сильного основания в среде ДМФ , совместно нейтрализуются две карбоксильные группы, затем - остальные две. Проблема определения последовательных термодинамических констант диссоциации электролитов, характеризуемых не только равновесными концентрациями, но и ионной силой и коэффициентами активности всех ионов электролита (а не всего электролита, как зачастую принимается), с точки зрения методологии остается одной из интересных в физической химии растворов сильных и слабых полиэлектролитов.

Новый подход к оценке ионной силы, коэффициентов активности всех равновесных частиц в титруемой системе

При теоретических расчетах и экспериментальных определениях термодинамических констант диссоциации многоосновных кислот ионная сила и коэффициенты активности всех ионов, образующихся при титровании полиэлектролитов, не учитывались. В целях упрощения модельных расчетов, в связи с невозможностью оценки концентрации всех равновесных частиц, в литературе рекомендовалось принимать во внимание изменение концентрации первого иона, образующегося при диссоциации полиэлектролита или при титровании его сильным, однофункциональным электролитом - титрантом [1, 2, 5]. Безусловно, это не может быть оправданно, так как приводит к значительным расхождениям расчетов и эксперимента. Например, коэффициент активности иона водорода при концентрации сильной кислоты С _m = 10 моль/1000 г Н 2 О равен 10.54, т.е. расхождение эксперимента от теории столь значительно (более чем в 10 раз), что в уравнение для константы диссоциации хлороводородной кислоты вместо концентрации иона Н + требуется вводить произведение концентрации на коэффициент активности - активность.

В данной работе осуществлен полный учет равновесных концентраций всех частиц в растворе с дальнейшим новым подходом к проблеме ионной силы раствора электролита, заключающимся в графическом представлении логарифмической диаграммы « lg ( активности гидроксония ) - lg С» [6, 7].

Показана возможность и плодотворность такой интерпретации во всем диапазоне изменения концентраций всех равновесных частиц в титруемом растворе при нейтрализации четырехосновной кислоты сильным основанием.

Определение термодинамических констант диссоциации полифункциональных электролитов при совместной нейтрализации сильноосновным титрующим агентом кислотных до сих пор было затруднено вследствие ряда факторов:

• -    невозможности дифференцированной оценки констант в буферных областях в связи с нивелированием «смеси» полиэлектролита;

• -    некорректной оценки ионной силы полиэлектролита, так как при титровании образуется группа трудно рассчитываемых по концентрациям частиц - ионов разной степени зарядности и, как следствие, из-за проблем наиболее приемлемого определения коэффициентов активности всех заряженных частиц, вносящих немалый вклад в расчеты величин термодинамических констант диссоциации.

Применение разработанной нами концепции на основе построенных логарифмических диаграмм дает возможность преодолеть отмеченные трудности .

Для определения термодинамических констант диссоциации многоосновных кислот воспользуемся методами прямой потенциометрии и потенциометрического титрования, как наиболее наглядными и оптимальными среди известных методов. При этом требуется учитывать основные количественные законы теории растворов электролитов : закон электронейтральности, закон сохранения материального баланса, правило стехиометрии и ряд других.

Существующие методы оценок ионной силы при кислотно-основном равновесии, в связи с затруднениями полного и объективного учета концентраций всех образующихся частиц, основаны на использовании концентрации первой ионизированной частицы, например, [ A ^-] для одноосновной; [ HA ^- ] для двухосновной; [ H 2 A ^- ] для трехосновной кислот и т.д. Очевидно, пренебрегать равновесными концентрациями остальных ионов в расчетах констант диссоциации не следует, так как зачастую равновесные концентрации более заряженных частиц в процессе диссоциации значительно превышает концентрации первых ионов. Как уже отмечалось, наиболее приемлемым и плодотворным является представление кривой титрования кислот в логарифмических координатах. Равновесные концентрации неоттит-рованной кислоты [ H 4 A ] и ионов [ Н 3 A ^-], [ H 2 A ²" ], [ HA 3 ], [ A ^4-], образующихся при титровании кислоты

H 4 A , могут быть определены на диаграммах - lg (активность гидроксония) – lgC . Оценка значения коэффициентов активности f 0 , f 1 , f 2 , f 3 , f 4 в уравнении (2) проводится разными методами, например, по закону Дебая [8]:

lg f i = - Az i ²I^1/2/( 1 +ВаI^1/2),                                            (4)

где A = 1.8246∙10⁶ /(εT)^3/2, B = ( 2 e²N A ∙1000)^1/2/( εk Б Т)^1/2, I – ионная сила раствора, определяемая в данном случае по известному уравнению: I = 0.5([HA^-]∙ z 1 ² + [ A^2- ]∙ z 2 ²), а – расстояние наибольшего сближения ионов.

Обоснование метода Дэвиса при оценке коэффициента активности ионов для определения ионных составляющих в растворах электролитов

При оценке коэффициентов активности наиболее приемлемым является уравнение Дэвиса [9]:

-lgf i = [A∙Z i ∙I^0.5/( 1 +I^0.5)]- 0.1 ∙I,                                                 (5)

так как метод Дебая - уравнение (4) - требует введения а – расстояний наименьшего сближения частиц, которые, строго говоря, являются неопределенными и обычно принимаемыми в пределах 5∙10^-8 см . Поскольку в растворе все частицы (даже нейтральные молекулы) находятся в сольватированном состоянии (молекулярные сольваты, сольватированные ионы, ассоциированные ионы и т.д.), то даже простая сумма радиусов сольватированных ионов (в первом приближении) не дает полной информации по расстояниям наименьшего сближения ионов и вряд ли будет постоянной для одних и тех же сольватированных катиона и аниона в разных растворителях и равной 5∙10^-8 см [10].

Коэффициент А определяется соотношением

A = ( 2 πN A ∙1000)^1/2/( e³/ 2.303 ∙ k Б ^3/2) ∙ ( 1 /ε^3/2T^3/2 ),                                   (6)

где N A – число Авогадро, k Б – постоянная Больцмана, ε – диэлектрическая проницаемость среды, Т – температура по Кельвину. Для ДМФ получена величина А = 1.6363.

Таким образом, уравнение Дэвиса устраняет неопределенность с расстоянием наименьшего сближения частиц и вполне приемлемо для расчетов коэффициентов активности ионов в водных, тем более в неводных, растворах, где в зависимости от природы растворителя одни и те же ионы характеризуются различными радиусами сольватных оболочек. Расчеты термодинамических констант диссоциации электролитов дают более достоверные результаты по сравнению с методом Дебая.

Термодинамические константы четырехосновных кислот в органических растворителях

Концептуальный подход к оценке ионной силы раствора электролита заключался в полном учете концентраций всех равновесных частиц в титруемой системе. Отметим еще раз, что для сложных систем, к которым относится титруемый полиэлектролит, традиционно применялась концентрация только первого диссоциированного иона полиэлектролита, несмотря на присутствие двух- и многозарядных ионов, так как не было предложено реального инструмента, позволяющего количественно оценить продукты диссоциации.

Четырехосновная кислота при нейтрализации функциональных групп с двумя скачками титрования

Четырехосновная этилендиаминотетрауксусная ( ЭДТА ) кислота в среде ДМФ титруется с двумя скачками потенциалов, причем первый скачок соответствует совместной нейтрализации первых двух карбоксильных групп, а второй – совместной нейтрализации остальных карбоксильных групп (рис. 1).

В таблице 1 представлены данные потенциометрического титрования 2.3705∙10^-3 М раствора ЭДТА 5.04∙10^-2 М раствором гуанидина в среде ДМФ, а также -lg a(SH⁺) , логарифмы равновесных концентраций всех частиц в растворе в процессе титрования, определенных из рисунка 2, их коэффициенты активности, рассчитанные по уравнению (5), рК i исследуемой поликислоты по уравнению (2) для многоосновных кислот.

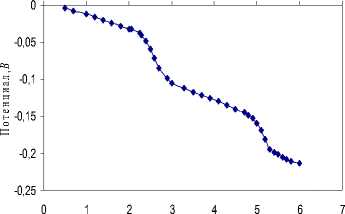
Объем титранта, мл

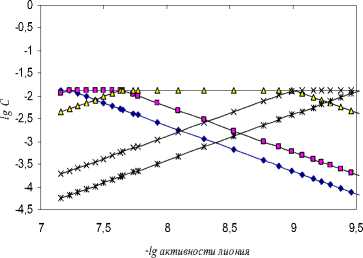
Рис. 2. Логарифмическая диаграмма «lg C – lg активности лиония» ЭДТА в ДМФ ( ◊ - [H 4 A], □ — [H 3 A ], А - [H 2 A² ], х - [HA^3-], * — [A^4-])

Рис. 1. Кривая потенциометрического титрования 3.37∙10-3М раствора

ЭДТА 0.0504М раствором гуанидина в ДМФ

Математическая обработка результатов, полученных при потенциометрическом титровании по термодинамическим константам диссоциации ЭДТА в среде ДМФ , приводит к доверительному интервалу, внутри которого с вероятностью 95% находятся показатели констант диссоциации [4.-Прил. IV]:

рК 1 = 7.44 ±0.06; рК 2 = 8.31± 0.18; рК 3 = 11.19 ± 0.19; рК 4 = 12.61 ± 0.26.

Данные для оценки термодинамических констант диссоциации ЭДТА в ДМФ

Таблица 1

Vi	E, В	-lg a(SH+)	lg [H 4 A]	lg[H 3 A-]	lg[H 2 A2-]	lg[HA3-]	lg[A4-]
0.5	-0.004	7.16	-1.8702	-1.9309	-2.3508	-3.7208	-4.2508
0.7	-0.008	7.23	-1.8773	-1.8702	-2.2830	-3.6530	-4.1830
1.0	-0.012	7.29	-1.9451	-1.8702	-2.2152	-3.5852	-4.1152
1.2	-0.016	7.36	-2.0129	-1.8702	-2.1474	-3.5174	-4.0474
1.4	-0.020	7.43	-2.0807	-1.8702	-2.0796	-3.4496	-3.9796
1.6	-0.024	7.50	-2.1485	-1.8702	-2.0118	-3.3818	-3.9118
1.8	-0.028	7.56	-2.2163	-1.8702	-1.9440	-3.3141	-3.8441
2.0	-0.032	7.63	-2.2841	-1.8702	-1.8763	-3.2463	-3.7763
2.2	-0.038	7.73	-2.3857	-1.9658	-1.8702	-3.1446	-3.6746
2.3	-0.040	7.77	-2.4196	-1.9997	-1.8702	-3.1107	-3.6407
2.4	-0.049	7.92	-2.5722	-2.1522	-1.8702	-2.9581	-3.4881
2.5	-0.059	8.09	-2.7417	-2.3217	-1.8702	-2.7886	-3.3186
2.6	-0.071	8.29	-2.9451	-2.5251	-1.8702	-2.5852	-3.1152
2.7	-0.085	8.53	-3.1824	-2.7624	-1.8702	-2.3480	-2.8780
2.9	-0.099	8.77	-3.4196	-2.9997	-1.8702	-2.1107	-2.6407
3.0	-0.106	8.89	-3.5383	-3.1183	-1.8702	-1.9920	-2.5220
3.3	-0.112	8.99	-3.6400	-3.2200	-1.8702	-1.8903	-2.4203
3.5	-0.117	9.07	-3.7247	-3.3048	-1.9347	-1.8702	-2.3356
3.7	-0.122	9.16	-3.8095	-3.3895	-2.0195	-1.8702	-2.2508
3.9	-0.126	9.23	-3.8773	-3.4573	-2.0873	-1.8702	-2.1830
4.1	-0.130	9.29	-3.9451	-3.5251	-2.1551	-1.8702	-2.1152
4.3	-0.135	9.38	-4.0298	-3.6098	-2.2398	-1.8702	-2.0305
4.5	-0.140	9.46	-4.1146	-3.6946	-2.3246	-1.8702	-1.9457
4.7	-0.145	9.55	-4.1993	-3.7793	-2.4093	-1.8793	-1.8702

Продолжение таблицы 1

Vi	I0.5	f 1	f 2	f 3	f 4	рК 1	рК 2	рК 3	рК 4
0.5	0.1268	0.6568	0.4298	0.2812	0.1840	7.40	8.13	-	-
0.7	0.1367	0.6383	0.4057	0.2579	0.1639	7.41	8.22	-	-
1.0	0.1439	0.6255	0.3893	0.2424	0.1509	7.42	8.25	-	-
1.2	0.1518	0.6117	0.3722	0.2264	0.1378	7.43	8.28	-	-
1.4	0.1607	0.5970	0.3543	0.2103	0.1248	7.44	8.31	-	-
1.6	0.1704	0.5816	0.3360	0.1941	0.1121	7.45	8.34	-	-
1.8	0.1811	0.5653	0.3172	0.1779	0.0998	7.46	8.38	-	-
2.0	0.1929	0.5483	0.2981	0.1621	0.0881	7.48	8.42	-	-

Продолжение таблицы 1

2.2	0.1931	0.5481	0.2978	0.1618	0.0879	7.42	8.43	-	-
2.3	0.1931	0.5481	0.2978	0.1618	0.0879	-	-	-	-
2.4	0.1950	0.5454	0.2949	0.1594	0.0862	-	-	-	-
2.5	0.2012	0.5368	0.2855	0.1519	0.0807	-	-	-	-
2.6	0.2151	0.5187	0.2661	0.1366	0.0701	-	-	-	-
2.7	0.2421	0.4863	0.2333	0.1119	0.0537	-	-	-	-
2.9	0.2839	0.4427	0.1924	0.0836	0.0363	-	-	-	-
3.0	0.3118	0.4176	0.1705	0.0696	0.0284	-	-	-	-
3.3	0.3399	0.3948	0.1517	0.0583	0.0224	-	-	11.06	12.40
3.5	0.3479	0.3887	0.1469	0.0555	0.0210	-	-	11.09	12.47
3.7	0.3534	0.3847	0.1438	0.0537	0.0201	-	-	11.12	12.50
3.9	0.3601	0.3799	0.1401	0.0516	0.0190	-	-	11.15	12.54
4.1	0.3690	0.3737	0.1353	0.0490	0.0177	-	-	11.18	12.60
4.3	0.3832	0.3641	0.1282	0.0451	0.0158	-	-	11.24	12.68
4.5	0.4011	0.3529	0.1200	0.0408	0.0138	-	-	11.32	12.78
4.7	0.4185	0.3425	0.1127	0.0370	0.0122	-	-	11.39	12.88

Во-первых, доверительный интервал в большинстве обработанных величин более узок, что свидетельствует о достаточно высокой воспроизводимости результатов. Во-вторых, учитываются равновесные концентрации всех частиц в системе в процессе переноса протона. В-третьих, этот метод более нагляден и подтверждается диаграммами. В-четвертых, при решении многих систем уравнений зачастую константы диссоциации оказываются отрицательными.

Таким образом, разработана теоретическая модель определения термодинамических констант диссоциации многоосновных кислот в растворителях и предложена методика экспериментального подтверждения модельных уравнений.