Исследование регрессионной модели в различных компьютерных средах
Автор: Баженов В.Р., Баженов Р.И.
Журнал: Экономика и социум @ekonomika-socium
Статья в выпуске: 3-1 (16), 2015 года.
Бесплатный доступ
В статье рассмотрено решение эконометрической задачи по регрессионному анализу. Произведено решение как традиционным, математическим способом, так и в различных компьютерных средах. Исследование показало, что применение MS Excel, Gretl, SPSS, EViews позволяет получить аналогичные результаты.
Регрессионная модель, анализ, эконометрика
Короткий адрес: https://sciup.org/140113598
IDR: 140113598
Текст научной статьи Исследование регрессионной модели в различных компьютерных средах
Построение прогностических моделей является достаточно актуальной задачей в современной экономике. Такая модель позволяет рассчитать различные требуемые параметры и минимизировать риски. Часто на практике применяется линейная регрессионная модель. Поэтому необходимо иметь доступный компьютерный инструмент, позволяющий в короткие сроки решить описываемую проблему.
Рассмотрим эконометрическую задачу, часто встречающую в различных пособиях [1].
По семи территориям Уральского региона за 199Х г. известны значения двух признаков (табл. 1.).
Таблица 1 – Значения расходов на покупку продовольственных товаров в общих расходах и среднедневной заработной платы одного работающего
|
Район |
Расходы на покупку продовольственных товаров в общих расходах, %, у |
Среднедневная заработная плата одного работающего, руб., х |
|
Удмуртская респ. |
70,3 |
44,1 |
|
Свердловская обл. |
61,7 |
57,5 |
|
Башкортостан |
60,9 |
56,7 |
|
Челябинская обл. |
58,2 |
60,8 |
|
Пермская обл. |
56 |
57,3 |
|
Курганская обл. |
54,8 |
46,2 |
|
Оренбургская обл. |
50,3 |
54,7 |
Требуется рассчитать параметры следующих линейной функций и оценить модель через среднюю ошибку аппроксимации A и F-критерий Фишера.
Рассмотрим математическое решение [2].
Для решения параметров a и b линейной регрессии y=a+bx решаем систему нормальных относительно a и b :
na + bX x = X y, a X x + b ^ x2 =£ yx.
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
a = y - b • x , b =
cov( x , y ) _ y j X y ' x
^x2
2 -2
x - x
.
Составим таблицу (табл.2) для вычислений.
Таблица 2 – Вычисления для линейной регрессионной модели
|
Номер региона |
y |
x |
y*x |
x^2 |
y^2 |
Yx |
Y-Yx |
Ai |
|
1 |
70,3 |
44,1 |
3100,23 |
1944,81 |
4942,09 |
62,46 |
7,84 |
11,1529 6 |
|
2 |
61,7 |
57,5 |
3547,75 |
3306,25 |
3806,89 |
57,57 |
4,13 |
6,68896 9 |
|
3 |
60,9 |
56,7 |
3453,03 |
3214,89 |
3708,81 |
57,86 |
3,04 |
4,98416 9 |
|
4 |
58,2 |
60,8 |
3538,56 |
3696,64 |
3387,24 |
56,37 |
1,83 |
3,14519 2 |
|
5 |
56 |
57,3 |
3208,80 |
3283,29 |
3136,00 |
57,65 |
-1,65 |
2,939 |
|
6 |
54,8 |
46,2 |
2531,76 |
2134,44 |
3003,04 |
61,69 |
-6,89 |
12,5796 8 |
|
7 |
50,3 |
54,7 |
2751,41 |
2992,09 |
2530,09 |
58,59 |
-8,29 |
16,4890 2 |
|
ИТОГО |
412,2 |
377,3 |
22131,5 4 |
20572,4 1 |
24514,1 6 |
412,20 |
0,00 |
57,98 |
|
Среднее |
58,89 |
53,90 |
3161,65 |
2938,92 |
3502,02 |
8,28 |
||
|
сигма |
5,87 |
5,81 |
||||||
|
сигма^2 |
34,50 |
33,71 |
В результате вычислений получилось b= - 0.36, a= 78.54.
Таким образом, уравнение регрессии: y=78.54-0.36·x. данную зависимость можно интерпретировать так, с увеличением среднедневной заработной платы на 1 руб., доля расходов на покупку продовольственных товаров снижается на 0.36 %-ных пункта.
Тесноту связи изучаемых явлений оценивает линейный коэффициент r... (-1 < r_< 1)
парной корреляции xy для линейной регрессии xy :
r xy = b ~ = ° y
cov( x , y ) _ y • x - y ■ x
° x ° y
2 -2
X - X
,
r = b ^ x- = -0,36047 ^ y
.
Средняя ошибка аппроксимации - среднее отклонение расчетных
A = 1 ^ y—y ^100% _ значений от фактических: n y , A = 8.28
Рассчитаем F-критерий:
F, = фа кт
X ( У - y ) 2 / m X y - у ) 2 / ( n - m - 1 )
2 rxy xy
( n - 2 ) = 0,746722
Полученное значение указывает на необходимость принять гипотезу о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
Можно заметить, что производиться достаточно много рутинных вычислений, поэтому посмотрим возможность решения в различных компьютерных средах.
Представим результат решения задачи в среде MS Excel [3] (рис.1).
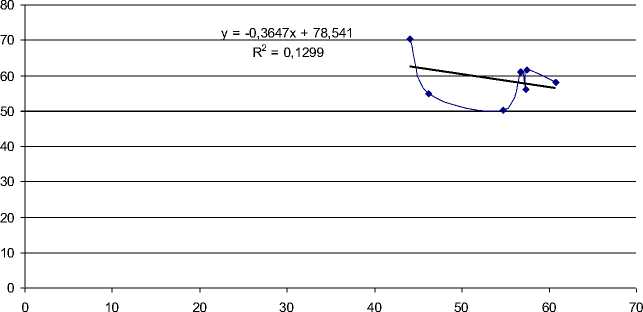
y
Линейный (y)
Рисунок 1 – Решение в MS Excel
Покажем результат решения в компьютерной среде Gretl [4, 5], разработанной специально для решения эконометрических задач (рис.2).
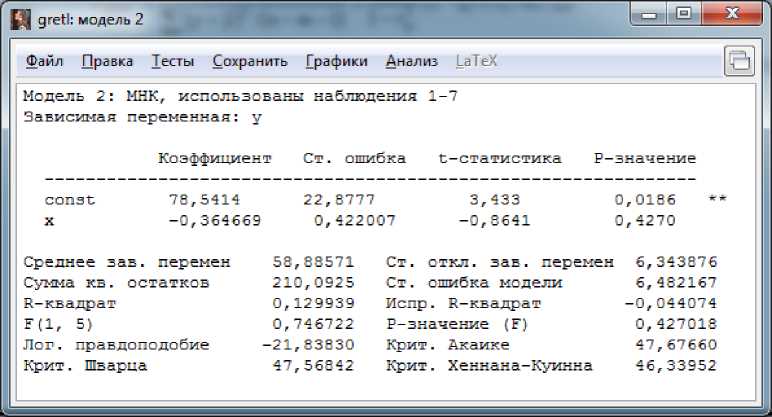
Рисунок 2 – Результат решения в Gretl
В популярной среде SPSS также имеется возможность строить различные регрессионные модели [6-8]. Представим линейную модель (рис.3).
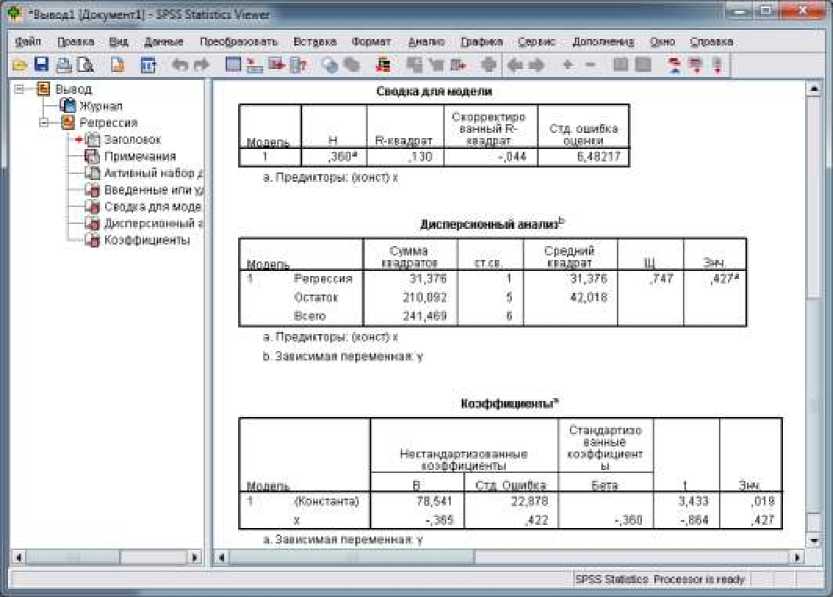
Рисунок 3 – Отчет в среде SPSS
Для построения эконометрических моделей часто используется среда EViews [9, 10]. Покажем результат построения линейной регрессионной модели (рис.4).
□ Equation: UNTITLED Workfile: 2::2\ | □ || В | ^|
I VjewJ Proc Object Print Name || Freeze Estimate Forecast Stats Resids
Dependent Variable: X
Method: Least Squares Date: 07/15/15 Time: 03:23 Sample: 1 7 Included observations: 7
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
Y |
-0.356320 |
0.412345 |
-0.864131 |
0.4270 |
|
C |
74.88214 |
24.40169 |
3.068728 |
0.0278 |
|
R-squared |
0.129939 |
Mean dependentvar |
53.90000 |
|
Adjusted R-squared |
-0.044074 |
S.D. dependent var |
6.270832 |
|
S.E. of regression |
6.407531 |
Akaike info criterion |
6.787781 |
|
Sum squared resid |
205.2823 |
Schwarz criterion |
6.772327 |
|
Log likelihood |
-21.75723 |
Hannan-Quinn criter. |
6.596770 |
|
F-statistic |
0.746722 |
Durbin-Watson stat |
0.502517 |
|
Pro b(F-stati stic) |
0.427018 |
Рисунок 4 – Результат решения в EViews
На основе анализа данных, представленных на рис. 1-4, можно заметить, что полученные результаты практически одинаковы. Исследователь для построения линейной регрессионной модели вправе использовать любую доступную ему компьютерную среду: Gretl (свободно распространяемая), MS Excel (платная), SPSS (платная), EViews (платная).
Список литературы Исследование регрессионной модели в различных компьютерных средах
- Яковлева Л.А. Эконометрика. Комплексное учебное пособие для студентов экономических специальностей заочного дистанционного обучения. Кемерово: Кемеровский технологический институт пищевой промышленности, 2002. 35 с. URL: http://e-lib.kemtipp.ru/uploads/29/pmii087.pdf
- Эконометрика/Под ред. И.И.Елисеевой. М.: Финансы и статистика, 2004. 344 с.
- Петросян Г.В., Баженов Р.И. Нахождения зависимости прогиба сплошного льда от скорости движения нагрузки на основе регрессионного анализа//Исследования в области естественных наук. 2015. № 6 . URL: http://science.snauka.ru/2015/06/10167 (дата обращения: 16.06.2015).
- Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска//Экономика и менеджмент инновационных технологий. 2015. № 4-1 (43). С. 72-80.
- Лагунова А.А., Баженов Р.И. Разработка в среде gretl регрессионной модели рынка вторичного жилья г. Биробиджана//Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
- Широкова Н.А., Баженов Р.И. Применение корреляционного анализа для исследования данных спортивных показателей студентов в среде SPSS//Nauka-Rastudent.ru. 2015. № 6 (18). С. 25.
- Муллинов Д.О., Винокуров А.С., Баженов Р.И. Разработка в среде SPSS регрессионной модели рынка автомобилей//Nauka-Rastudent.ru. 2015. № 6 (18). С. 24.
- Лагунова А.А., Муллинов Д.О., Баженов Р.И. Применение программной среды SPSS для исследования данных психологических методик//Психология, социология и педагогика. 2015. № 6 . URL: http://psychology.snauka.ru/2015/06/5446 (дата обращения: 24.06.2015).
- Муллинов Д.О., Баженов Р.И. Разработка в среде eviews регрессионной модели рынка гаражных помещений г. Биробиджана//Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
- Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды eviews//Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.