Исследование режимов течения жидкостей в гидравлических системах трансмиссий транспортных машин

Для описания гидротрасс в гидравлических системах трансмиссий большое значение имеют выяснение физической картины течения, выявление режимных зон и областей их существования.

В реальных трансмиссиях жидкость подается во внутренние полости валов, а затем через сверления в них поступает к месту назначения. Гидравлические диаметры внутренних полостей валов обычно значительно больше, чем у дозирующих радиальных и осевых каналов. Учитывая это обстоятельство, в первом приближении сопротивлением полостей валов по сравнению с сопротивлениями дозирующих каналов можно пренебречь.

Решение задачи по определению пропускной способности каналов будем искать экспериментальным путем с применением теории подобия и метода анализа размерностей [3, 4].

Примем, что пропускная способность Q подводящих каналов является функцией всех переменных и размерных постоянных, которыми определяется течение рабочей жидкости.

Определительное уравнение для пропускной способности запишем в виде

Q=f( О , , P, F, l),                                       (1)

где р,    плотность и кинематическая вязкость рабочей жидкости; P перепад давления рабочей жидкости; F, l площадь сечения и длина канала.

В подводящих каналах жидкость полностью заполняет его объем, поэтому из уравнения исключено ускорение свободного падения.

Запишем определительное уравнение по методу Реллея [4] в степенном виде:

Q=A хр ab X. P^c XFXl^e.                           (2)

В качестве основных единиц измерения определяющих параметров примем следующие: М масса; Т время; L длина.

Размерности всех параметров уравнения (2) будут следующими:

[ Q ]= L³T^-1 ;

[ р ]= ML ^{- 3} ;

[ и ]= L²T^-1 ;

[ P ]= ML^-1T^-2 ;

[ d ]= L ;

[ l ]= L .

Учитывая равенство размерностей левой и правой части уравнения (2), напишем систему уравнений, составленную из показателей степеней при основных единицах измерения

L 3   3 a + 2 b c +d+e

M     0 a+c

T - 1 -b - 2c и, положив известными c и e, найдем a=-c; b=1-2c; d=1+2c-e. Группируя члены с одинако- выми показателями, получим

QA

Pd ² ; ^c

le d

.

Комплекс в левой части уравнения (3) представляет собой число Рейнольдса, определяемое расходной скоростью

Q  их L ²   их L

Re , dvXLv где ν скорость течения жидкости; L характерный линейный размер.

ΔPd2

Выражение       представляет собой соотношение сил давления, инерции, трения:

рv2

Pd2 F    F давл     ин

, р2, тр     тр где Fдавл  PXd2  сила давления жидкости; F ~ рd 2v2  сила инерции жидкости; F ~ирdv сила вязкостного трения.

FF

Причем:  ин = Re критерий Рейнольдса;  давл =k имеет физический смысл гидравли- тр                                        тр ческого коэффициента трения.

В уравнении (3) показатели степеней c и e и коэффициент A неизвестны и подлежат экспериментальному определению.

Логарифмируя выражение (3), получим линейное уравнение регрессии относительно неизвестных коэффициентов c, e, A lg Q lg A +cX lg d

Pd ²

l

+e X lg . d

Удельный вес рабочей жидкости определяется по формуле (5) / ⁼ /₀   k(t-t ₀ ),

где у 0 удельный вес рабочей жидкости при температуре t 0 ^сC; t текущее значение температуры.

Таблица

Значение коэффициента пропорциональности «k» в зависимости от величины у 0

Y0 кг/м3	700	750	800	850	900	950
k	0,9	0,83	0,77	0,69	0,63	0,57

Для определения кинематической вязкости жидкости при различных температурах используется номограмма Вальтера-Семенидо [2, 5], соответствующая уравнению:

lglg(v+0,6)=A +BxlgT, где T абсолютная температура масла; А, В постоянные для данного масла коэффициен- ты, определяемые опытным путем.

Номограммы строились опытным путем по двум значениям кинематической вязкости масла, определенных с помощью вискозиметров Пинкевича при температуре окружающего воздуха и при 100 С.

Методика проведения экспериментов обеспечивала минимизацию влияния на измеряемую величину случайных факторов, например параметров неустановившихся процессов, связанных с перестройкой потоков при ступенчатом изменении частоты вращения. В этом случае перед изменениями производилась выдержка по времени до 10 мин, чтобы исключить корреляцию смежных наблюдений.

Исследовались следующие уровни перепадов давления: (16;45;75);×104 Па, вязкостей (0,4:1,2:2,0;2,2)×10-4(м2/с).

Обработка экспериментальных данных проводилась методом наименьших квадратов в программной среде Microsoft Excel. Результаты обработки приведены на рисунке.

Испытания позволили установить, что при течении жидкости через подводящие каналы наблюдаются две ярко выраженные зоны с точкой перехода, соответствующей Pd²

lg       5,15. Из графика (рис.) видно, что экспериментальные точки, снятые при различ- ных вязкостях и перепадах давления в двух зонах, хорошо согласуются с видом полученной математической модели.

В результате статистической обработки экспериментальных данных получено уравнение регрессии для пропускной способности подводящих каналов для I зоны:

Q _A vd ¹

0,662

Pd2  ,

; A 1    28,73;

для ΙΙ зоны:

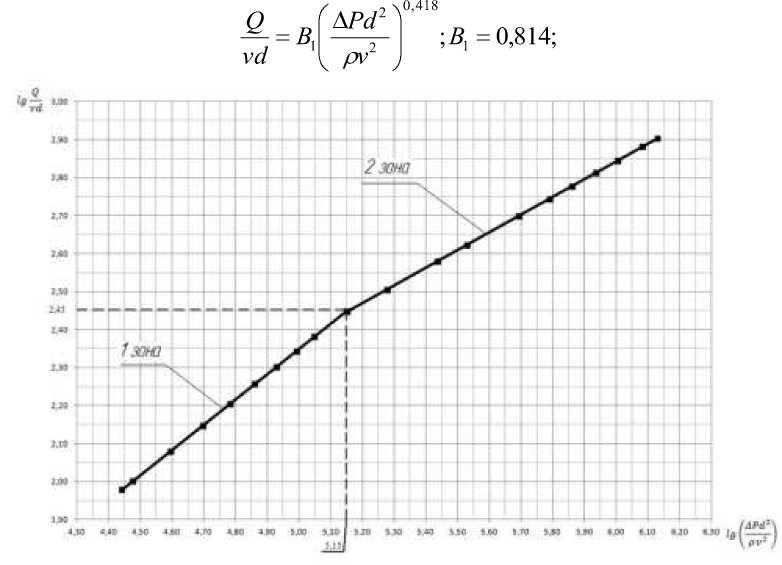
Рис. График зависимости комплекса расхода (  ) от комплекса давления (       )

vd                            v ²

Переход из Ι во ΙΙ зону осуществляется при lg      =5,15.

рv ²

Влияние симплекса на пропускную способность подводящих каналов не проявилось, т.е. коэффициент l оказался незначимым. Это свидетельствует о том, что сопротивлением трения можно пренебречь и расход жидкости определяется лишь местными сопротивлениями в диапазоне =1,0 … 10. d

Вторая зона представляет собой широко известную в гидравлике зону турбулентного течения жидкости, когда соблюдается квадратичная зависимость между перепадом давления и расходам. Вследствие возмущающего действия многочисленных поворотов, а также сужений и расширений критическим числом Рейнольдса, при котором наступает турбулентный режим течения для подводящих каналов, является Re=280, это значение Re хорошо согласуется с данными, полученными для золотниковых распределителей Т.М. Баштой [1]. Потери полного давления в любом сложном элементе гидротрассы с физической точки трения неразделимы. Однако для удобства расчета их часто в одном и том же элементе трассы условно разделяют на местные потери (ΔP м ) и потери трения (ΔP тр ). При этом считают, что местные потери (местное сопротивление) сосредоточены в одном сечении, хотя на самом деле они распространяются на сравнительно большую длину, за исключением, конечно, случая выхода потока из трассы.

В современных гидравлических расчетах обычно оперируют безразмерным коэффициентом гидравлического сопротивления, весьма удобным тем, что в динамически подобных потоках он имеет одно и то же значение независимо от рода жидкости, скорости потока и размеров рассчитываемых участков.