Исследование RQ-системы 1 с r-настойчивым вытеснением альтернативных заявок

Введение. Применение классических моделей теории массового обслуживания для повышения надежности прогнозирования и обработки информации телекоммуникационных, вычислительных и экономических систем не всегда дает адекватные результаты. Поэтому для анализа и исследования таких систем используют более адекватные модели с повторной очередью (Retrial Queueing System). Между повторами заявки (клиенты) находятся в источнике повторных вызовов (ИПВ). Обзор работ по этой тематике приведен в работах [1-3]. Также модели с повторными вызовами широко применяются для проектирования и оптимизации информационно-коммуникационных систем различного уровня, цифровых сетей связи, управляемых протоколами случайного множественного доступа, в call-центрах, для оптимизации работы транспортных систем и во многих других областях.

В данной работе рассматривается RQ-система с двумя входящими потоками и приоритетом заявок. Такая система массового обслуживания служит моделью протокола случайного множественного доступа космической сети связи с двумя потоками конкурирующих сообщений. В работах [4-11] рассматриваются системы с повторными вызовами, в которых 2 типа входящих заявок, которым назначаются приоритеты. Для рассматриваемых систем найдены основные вероятностно-временные характеристики. S. R. Chakravarthy, A. Dudin [12] рассматривают систему, в которой 2 типа входящих потоков (заявки 1 и 2 типов) и при этом назначается приоритет заявкам 1 типа, которые в дальнейшем образуют очередь, а заявки 2 типа уходят в ИПВ. Заявки также приходят пачками. Для данной модели найдено совместное распределение числа заявок в очереди и в ИПВ. В вышеуказанных работах приоритет рассматривается в том смысле, что какому-то одному типу заявок разрешается обслуживание в порядке приоритета, в то время как другим приходится находиться в ИПВ, ожидая обслуживания всех приоритетных заявок. Системам с приоритетами заявок, в классическом понимании, посвящено немало работ. Основные результаты могут быть найдены в [13-17].

В предлагаемой работе изучена система, в которой можно назначать приоритеты через вероятности.

Постановка задачи. Рассмотрим RQ-систему с двумя входящими простейшими потоками (рис. 1), произвольным временем обслуживания и вытеснением альтернативных заявок.

На вход RQ-системы поступают два простейших потока заявок с параметрами X 1 и X ₂ соответственно. Если прибор свободен, то пришедшая заявка занимает прибор для обслуживания в течение случайного времени с функциями распределения B 1 ( x ) и B ₂ ( x ), соответственно.

Если в момент прихода заявка первого типа обнаруживает прибор занятым заявкой первого типа, то она уходит в ИПВ 1 (источник повторных вызовов для заявок первого типа), где осуществляет случайную задержку, распределенную по экспоненциальному закону с параметром O 1 . После случайной задержки заявка вновь обращается к прибору с повторной попыткой его захвата. Если же в момент прихода заявка первого типа обнаруживает прибор занятым заявкой второго типа, то пришедшая заявка с вероятностью r 1 вытесняет заявку второго типа, которая уходит в ИПВ2, а сама встает на обслуживание, иначе с вероятностью 1 - r 1 уходит в ИПВ1, где осуществляет случайную задержку.

Если в момент прихода заявка второго типа обнаруживает прибор занятым заявкой первого типа, то пришедшая заявка с вероятностью r ₂ вытесняет заявку первого типа, которая уходит в ИПВ1, а сама встает на обслуживание, иначе с вероятностью 1 - r ₂ уходит в ИПВ2 (источник повторных вызовов для заявок второго типа), где осуществляет случайную задержку, распределенную по экспоненциальному закону с параметром о ₂. После случайной задержки заявка вновь обращается к прибору с повторной попыткой его захвата.

ИПВ1

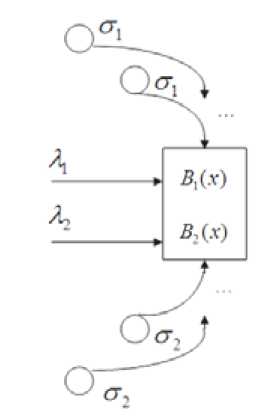
ИПВ2

Рис. 1. RQ-система M ⁽²⁾ | B ( x )⁽²⁾ | 1

Таким образом, происходит r -настойчивое вытеснение ( r -persistent exclusion) альтернативных заявок. При обращении заявок из ИПВ1 и ИПВ2 r -настойчивое вытеснение происходит аналогичным образом.

Обозначим zKt) - число заявок в ИПВ1, i2(t) - число заявок в ИПВ2, k(t) определяет состояние прибора следующим образом:

0, если прибор свободен, k (t) = '

• 1,    есди прибор занят заявкой первого типа,

• 2,    если прибор занят заявкой второго типа.

Ставится задача нахождения среднего числа заявок в ИПВ1, ИПВ2 и распределения вероятностей состояний прибора.

Система уравнений Колмогорова. Так как процесс { k ( t ), i 1 ( t ), i ₂( t ) } не является марковским, то рассмотрим процесс с переменным числом компонент.

Если k ( t ) = 0 , то рассматриваем процесс { k ( t ), i 1 ( t ), i ₂ ( t ) } . Если k ( t ) = n , n = 1, 2, то рассматриваем процесс { k ( t ), i 1 ( t ), i ₂( t ), z ( t ) } , где z ( t ) - остаточное время от момента t до момента окончания обслуживания.

Обозначим P { k ( t ) = 0, i₁ ( t ) = i 1 , i ₂ ( t ) = i ₂ } = P₀ ( i 1 , i ₂, t ) вероятность того, что прибор в момент времени t находится в состоянии 0 , в ИПВ1 находится i 1 заявок, в ИПВ2 находится i ₂ заявок; P { k(t ) = n , i 1 ( t ) = i 1 , i ₂( t ) = i ₂, z ( t ) <  z } = P_n ( i₁, i ₂, z , t ), n = 1, 2, вероятность того, что прибор в момент времени t находится в состоянии n , в ИПВ1 находится i 1 заявок, в ИПВ2 находится i ₂ заявок, остаточное время обслуживания меньше z .

Для распределения вероятностей {P0(i1, i 2, t), P(ivi2,z,t),P2(i1,i2,z,t)}, применяя формулу полной вероятности, запишем равенства:

P 0 ( i 1 , i 2 , t + A t ) = P 0 ( 4 , i 2 )(1 - X A t )(1 - X 2 A t ) X x (1 - i ₁ o ₁ A t )(1 - i₂ o ₂ A t ) + P 1 ( i 1 , i ₂, A t , t ) + + P ₂ ( i 1 , i ₂, A t , t ) + o ( A t ),

P 1 ( i 1 , i ₂, z - A t , t + A t ) = P ₀( i 1 , i ₂, t ) X 1 A tB 1 ( z ) + + P 0 ( i 1 + 1, i 2 , t )( i 1 + 1) 0 1 A tB ( z ) + + [ P 1 ( i 1 , i 2 , z , t ) - P 1 ( i 1 , i 2 , A t , t ) ] x x (1 - X 1 A t )(1 - X 2 A t )(1 - i 2 O 2 A t ) + + P ₂ ( i 1 + 1, i ₂ - 1, » , t )( i 1 + 1) o 1 A tB 1 ( z ) r 1 + + P 2 ( i 1 , i 2 - 1, ” , t ) X 1 A tB 1 ( z ) r_x + + P 1 ( i 1 - 1, i ₂, z , t ) X 1 A t + P 1 (i 1 , i ₂ - 1, z , t ) X ₂ A t (1 - r ₂) + + P ⁽ 1 1 , ^z 2 , z , t ) ^z 2 ° 2 ^a t ^{(1 - r} 2 ) + ^{o ( A} t ),

P ₂ ( i 1 , i ₂, z - A t , t + A t ) = P ₀ ( i 1 , i ₂, t ) X ₂ A tB ₂ ( z ) +

+ P 0 ^{( z}1 , ^z 2 + 1, t ^{)( z} 2 + ^{1) o} 2 ^{A tB} 2 ^{( z} ) +

+ [ P > ( i 1 , i 2 , z , t ) - P₂ ( i 1 , i 2 , A t , t ) ] (1 - X 1 A t ) x

x (1 - X ₂ A t )(1 - i ₁ o ₁ A t ) + P 1 ( i 1 - 1, i ₂ + 1, ” , t ) x

^{x ( z} 2 + ^{1) o} 2 ^{A tB} 2^{( z} ) ^r 2 + ^P 1^{( Z} 1 ^- 1, ^Z 2 , ” , t ^{) X} 2 ^{A tB} 2^{( z} ) ^r 2 ⁺ + P₂ ( i 1 , i ₂ - 1, z , t ) X ₂ A t + P ₂ ( i 1 - 1, i ₂, z , t ) X 1 A t (1 - r 1 ) +

+ P ₂ ( i 1 , i ₂, z , t ) i ₁ o ₁ A t (1 - r 1 ) + o ( A t ).

Откуда прямая система дифференциальных уравнений Колмогорова имеет вид

^{- ( X} 1 +^X 2 ^{+ Z} 1 ^G 1 ^{+ Z} 2 ^О 2 ) ^P 0^{( i} 1^{, Z} 2 , t ) ⁺

₊ a P 1 (i_x, i 2 ,0, t ) ₊ a P 2 (i 1 , i 2 ,0, t ) = a P 0 ( i 1 , i 2 , t )

az              az              at     '

X 1 B 1 ( z ) P 0 ( i 1 , i 2 , t ) + ( i_x + 1) 0 1 B_x ( z ) P 0 ( i_x + 1, i 2 , t ) -

^{- ( X} 1 + ^X 2 ^{+ Z}2 ° 2 ) ^P 1 ^{( Z} 1 , ^Z 2 , ^z , t ) ⁺

+ ( i '1 + 1) 0 1 r.B 1 ( z ) P 2 ( i_x + 1, i 2 - 1, ” , t ) +

+X 1 Г 1 B_x ( z ) P₂ ( i ₁, i 2 - 1, ” , t ) + X 1 P 1 ( i_x - 1, i 2 , z , t ) +

+(1 - Г2 )X2P1 (i1, i2 -1, z, t) + (1 - Г2)i2^2P1 (i1, i2, z, t) + aP1(i1,i2,0,t) aP1(i1,i2,z,t)! az1,z2,z,t)

a z            a z             a t

1 2 B 2 ( z ) P_o ( i 1 , i 2 , t ) + ( i 2 + 1) 0 2 B 2 ( z ) P o ( i 1 , i 2 + 1, t ) " ^{- ( 1} 1 ^{+ 1} 2 ⁺ i 1 ⁰ 1 ) P 2⁽ i 1 , i 2 , z , t ) ⁺

^{+ (} i 2 ^{+ 1) o} 2 r 2^B 2 ⁽ z ) ^P1 ⁽ i 1 ^{- 1} i 2 ^{+ 1} ” , t ) ⁺ +1 2 Г 2 B 2 ( Z ) P ( i 1 - 1, i 2 , ” , t ) + X 2 P 2 ( i 1 , i 2 - 1, Z , t ) + + ^{(1 - r} 1 ^{) 1} 1 ^P 2 ⁽ i 1 ^- 1, i 2 , z , t ) ^{+ (1 - r} 1 ) i 1 ⁰ 1 ^P 2 ⁽ i 1 , i 2 , z , t ) ⁺ = a P 2 ( i 1 , i 2 ,0, t ) _- a P 2 ( i 1 , i 2 , z , t ) ₊ a P 2 ( 4, i 2 , z , t ) a z               a z                a t      "

Пусть в системе (1)

¹ im ” ^P o⁽ i 1 , i 2 , t ) = ^P o⁽ i 1 , i 2 ), lim P n ( i 1 , i 2 , z , t ) = P n ( i 1 , i 2 ), n = 1,2. t ^”

Тогда систему запишем в стационарном режиме следующим образом:

^{- ( 1} 1 ^{+ 1} 2 ⁺ i 1 ⁰ 1 ⁺ i 2⁰2 ) ^P 0 ⁽ i 1 , i 2 ) ⁺

, a p ( i 1 ,i 2 ,0) ₊ a P 2 ( i 1 , i 2 ,0) = ₀ a z             a z         ’

1 1 B ( z ) P 0 ( i 1 , i 2 ) + ( i 1 + 1) 0 1 B ( z ) P 0 ( i 1 + 1, i 2 ) -- ( 1 1 + 1 2 + i 2 0 2 ) P 1 (i 1 , i 2 , z ) +

^{+ (} i 1 ^{+ 1) o} 1 ^r 1 ^B 1 ^{( z} ) ^P 2 ⁽ i 1 ⁺ 1, i 2 ^- 1, ” ) ⁺ +1 1 rB ( z ) P 2 ( i 1 , i 2 - 1, ” ) +1 1 P 1 ( i 1 - 1, i 2 , z ) + + ^{(1 - r} 2 ) ^ 2 ^P 1 ⁽ i 1 , i 2 ^- 1, ^z ) ^{+ (1 - r} 2 ) i 2 ° 2^P1 ⁽ i 1 , i 2 , ^z ) ⁺

_ a P ( i 1 , i 2 ,0) a P 1 (i 1 ,i 2 , z )                  ₍₂₎

a z             a z     ’

1 2 B 2 ( z ) P 0 ( i 1 , i 2 ) + ( i 2 + 1) 0 2 B 2 ( z ) P 0 ( i 1 , i 2 + 1) -^{- ( 1} 1 ⁺¹ 2 ^{+ i} 1 ° 1^{) P} 2⁽ i 1 , i 2 , ^z ) ⁺

^{+ (} i 2 ^{+ 1) o} 2 ^r 2 ^B 2 ^{( z} ) ^P 1 ⁽ i 1 ^- 1, i 2 ⁺ 1, ” ) ⁺ +1 2 Г 2 B 2 ( z ) P ( i 1 - 1, i 2 , ” ) + 1 2 P 2 ( i 1 , i 2 - 1, z ) + ^{+ (1 - r} 1 ^{) 1} 1 ^P 2 ⁽ i 1 ^- 1, i 2 , ^z ) ^{+ (1 - r} 1 ) i 1 ° 1 ^P 2 ⁽ i 1 , i 2 , ^z ) ⁺ _ a P 2 ( i 1 , i 2 ,0) a P 2 ( i 1 , i 2 , z ) a z              a z     '

Уравнения для частичных характеристических функций. В силу системы (2) запишем систему уравнений для частичных характеристических функций следующего вида:

H 0 ( U 1 , и 2 ) = jr jr j ¹ e^{ju 2}i² P 0 ( i 1 , i 2 ), i "1 ⁼0 i 2 = 0

aH0( и1, и 2) aH1( и1, и 2,0)^ aH2( и1, и 2,0) n + j 03            +              +              — 0, a и 2            az             az aH(и,и2, z)

• ^{- ( 1} 1 ^{+ 1} 2 ) ^H 1 ^{( и} 1 , ^и 2 , ^z ) ⁺ j ⁰ 2 ^r 2-----

• a и 2

• - j 0 1 e ^j B 1 ( z ) ^a H ^{0( и} 1 , ^{и 2)} + a и 1

^{+ (1 - r} 2^{) 1} 2 e j ^{2 H} 1^{( и} 1 , ^и 2 , ^z ) ⁺               (3)

+1 1 B 1 ( z ) H ₀ ( и 1 , и ₂) +1 1 e j"¹ H 1 ( и 1 , и ₂, z ) +

⁺ r 1 ¹ 1 e^{J j 2} B 1^{( z} ) H 2 ⁽ " 1 , " 2 ) ^{- j} r 1 ⁰ 1 B 1^{( z} ) e^{j ( и 2 - и} 1 ) x a h ₂ ( и 1 , и ₂) a h 1 ( и 1 , и ₂,0) a h 1 ( и 1 , и ₂, z)

a " 1      =      a z              a z      ’

T2 , mj Т        л ,       ^{a H} 2⁽ " 1 , " 2 , ^z )

• ^{- ( 1} 1 ⁺¹ 2 ) ^H 2⁽ " 1 , " 2 , ^z ) ^{+ j 0} 1 ^r1

a " 1

• ^{- j 0} 2 ^B 2 ^{( z} ) e ^- j" ^{2 a H} °д " 1 , " ^{2 ) + (1 - r} 1 ^{) 1} 1 e j" ^{1 H} 2 ⁽ " 1 , " 2 , ^z ) ^{+ a} "  2

⁺¹ 2 ^B 2 ^{( z} ) ^H 0 ⁽ " 1 , " 2 ) ^{+ 1} 2 e j ^{2 H} 2 ⁽ " 1 , " 2 , ^z ) ⁺

+r212 B2(z ) ej"1 H1( "1, " 2) - jr202B2(z ) ej ( "1-" 2) x ah1("1,и2) ah2("1,и2,0) ah2("1,и2,z)

a и ₂     ~       a z               a z      ’

Аналитически данную систему решить затруднительно. Будем решать ее методом асимптотического анализа [18] в условии большой задержки ( 0^ 0), полагая, что 0 1 = 0у 1 , 0 2 = 0у ₂ .

Асимптотическое решение системы (3). В системе (3) сделаем замены:

⁰ m =⁰Y m ; ⁰ = е ; " m =S w m , m = 1, ² ;

H 0 ( " 1 , "  2 ) = F n ( W 1 , W 2 , s ),

” ”

H n ( U 1 , и 2 , z ) = X S e ju ¹⁴ e j 2 ' 2 P 0 ( 4 , i 2 ,z ), n = 0, 1, 2,

1 = 0 i 2 = 0

H n ( " 1 , "  2 , z ) = F n ( W 1 , W 2 , z , s ), n = 1, 2.

Система (3) перепишется следующим образом:

Л X Z         х        a F ₀ ( W , , w ₂, s )

-(11 + 12 )F0 ( W1, W2, s) + jY1-----Z a w1

aF0(w1,w2,s) af(w,w2,0,s) +j У2 —z----+----- a "w2

af,(w1,w2,0,s) n +       az

где j = V-1 — мнимая единица.

Обозначим

H n ( U 1 , и 2 , ” ) = H n ( U 1 , и 2 ), n = 1, 2,

^{- ( 1} 1 ^{+ 1} 2 ) ^F 1 ^{( W} 1 , w 2 , ^z , ^{s ) + j} У 2 ^r 2

a F 1 ( w 1 , w ₂, z , s )

^{a w} 2

—

^{- j} У 1 ^B 1^{( z} ) ^e

, - j s w ^{a F} 0^{( w}1 , ^w 2 , ^{s )} ₊

a w 1

a H n ( U 1 , и 2 ,0) = a H n ( U 1 , и 2 , z ) a z              a z

Запишем систему для частичных характеристических функций:

• ^{- ( 1} 1 ⁺¹ 2 ) ^H 0^{( и} 1 , ^и 2 ) ^{+ j О} 1---⁰^ 1 , 2^ ⁺

a и1

^{+ (1 - r} 2 ^{) 1} 2 e j ^s w ^{2 F} 1 ^{( W}1 , ^W 2 , ^z , ^{s ) + 1} 1 ^B 1 ^{( z} ) ^F 0 ^{( W}1 , w 2 , ^{s ) +} (₄) +1 1 e^{J s w} F 1 ( w 1 , w 2 , z , s ) + Г 1 1 1 B 1 ( z ) e ^s w ² F , ( w 1 , w 2 , s ) -

• - Jr ₁ y ₁ B 1 ( z ) e*' 2 - * ^a F 2 < w l2 w M> = a w 1

= a F 1 (' 1 ,w ₂,0, s ) a F 1 ( ' 1 ,' 2 ,z , s ) a z                 a z       ’

• ^{- ( k} 1 + ^k 2 ) F 2 ( ^W1 ^- w 2 ,z, ^{s ) +} j У 1 ^r 1    ² 1--

• 0 W1

• - j у 2 B 2 (z) e j ■ ⁰ F « ⁽ W ^1- w ²' ^{S )} + ^{0 w}2

+ ^{(1 - r}1 ^{) k} 1 e j ^S w F 2^{( w} 1^{- w} 2^- z ^{- S )} + ^k 2 B 2 ^(z) F 0 ^{( W} 1^{- W} 2^{- S ) +} +k ₂ e j ^{S w 2} F ₂ ( w ₁, w ₂,z, s ) + r ^k^ B ₂ (z) e j ^S w ¹ F ( w ₁, w ₂, s ) -

- jr 2 у 2 B 2 (z) e^{j s(} w ^{1 -} w ^{2) 0 F1 (}W ^1- w ^{2- S )} _

^{0 w} 2

_ 0 F , ( W 1 - W 2 -0- S ) 0 F 2 ( W 1 - W 2 -z- s ) 0 z                 0 z        ■

Обозначим x m , m _ 1-2 - асимптотическое среднее значение числа заявок в m -м источнике повторных вызовов, R k , k _ 0- 1- 2, - распределение вероятностей состояний прибора. Ниже будет показано- что R k - k _ 0- 1- 2- определяется значениями x m - m = 1- 2-поэтому будем применять обозначение R k ( x ₁- x ₂)- k _ 0- 1- 2.

Сформулируем следующее утверждение.

Теорема . Предельное (при s ^ 0 - z ^ го ) значение { F 0⁽ w 1^- w 2^{)- F} 1^{( w} 1^{- w} 2^{)- F} 2^{( W} 1^{- W} 2⁾ } р ^ешения { F 0^{( w} 1^{- w} 2^{- S )-} F 1 ( w ₁- w ₂- z - s )- F ₂( w ₁- w ₂- z - s ) } системы уравнений (4) имеет вид

^F 0 ^{( W} 1^{- w} 2 ) ^_ R 0 ^{( x} 1^{- x} 2 ) ^eX P ^{{ jW} 1 ^x 1 ^{+ jW} 2 ^x 2 ^{} -}

^F 1 ^{( W} 1^{- w} 2 ) ^_ R 1 ^{( x} 1^{- x} 2 ) ^eX P ^{{ jW} 1 ^x 1 ^{+ jW} 2 ^x 2 ^{} -}

^F 2^{( W} 1^{- w} 2 ) ^_ R 2 ^{( x} 1^{- x} 2 ) ^eX P ^{{ jW} 1 ^x 1 ^{+ jW} 2 ^x 2 ^{} -} где x - x ₂ являются решением системы уравнений

• ^-у 1 x 1 R 0⁽ x 1 - x 2 ) + ^{( k} 1 + r ^k^ + ^r 2 ^у 2 x 2 ) R 1⁽ x 1 - x 2 ) +

+ ^{( - Г} 1 У 1 ^x 1 + ^{(1 - r} 1 ^{) k} 1 ) R 2 ^{( x} 1^- x 2 ) ^{_ 0-}

• ^-y 2 ^x 2 R 0 ^{( x} 1^{- x}2 ) + ^{( - r} 2 У 2 ^x 2 + ^{(1 - r} 2^{) k} 2 ) R 1 ^{( x} 1^{- x} 2 ) + (5) + ^{( k} 2 + ^r 1 ^k 1 + ^Г 1 У 1 x 1 ) R 2 ^{( x} 1^- x 2 ) ^{_ 0-}

• а Rk (x1- x2) - k _ 0- 1- 2- определяются равенствами

r 1 _.       1 -B1*(r2(k2 +У2x2))_

R0(x1-x2) _ 1 k1*

^r 2^{( k} 2 +У 2 x 2 ) B 1 ^{( r} 2^{( k} 2 +У 2 x 2 ))

,        ^{1 -} B 2*^{( r} 1^{( k} 1 +У 1 ^x 1 ))

k 2                    *

^r 1^{( k} 1 +У 1 ^x 1 ) B 2^{( r} 1^{( k} 1 +У 1 ^x1⁾⁾

t,,..        ,       ^{1 -} B 1*^{( r} 2^{( k} 2 +У 2 x 2 ))

R , ( x x 2 ) .2 ,      ^{1 -} B =^{( r} 1 ⁽ k 1 ^+у 1 x 1 ⁾⁾     -    (6)

^r 1^{( k} 1 +У 1 ^x 1 ) B 2^{( r} 1^{( k} 1 +У 1 ^x 1 ))

R 0 ( x 1 - x 2 ) + R 1 ( x 1 - x 2 ) + R 2 ( x 1 - x 2 ) _ 1 .

X

B 1* ( r 2 ( k 2 +у 2 x 2 )) _ J e ^{- r 2(k2 +У2} x ²⁾ z dB 1 ( z )- 0

X

B 2* ( г , ( k 1 + У 1 x 1 )) _ J e ^{- r 1 (k1 +У1} x ¹) ^zdB 2 ( z ) - 0

преобразования Лапласа-Стилтьесса от функций распределений B ₁( x ) и B ₂( x ) в точках r ₂( k ₂ +у ₂ x ₂) и r ₁( k ₁ +у ₁ x ₁) соответственно.

Численная реализация. Были рассмотрены примеры численного решения системы (5) и численной реализации формул (6) для различных функций распределений B ₁ ( x ) - B ₂ ( x ) и различных значений параметров k ₁ - k ₂ и о ₁ - о ₂ .

В частности- рассмотрены взвешенные суммы гамма- и экспоненциальных распределений

B 1* ( x ) _ 9 1 (1 + - x Г¹ + (1 - 9 1 )(1 + - ) ^-1 -

Р 1                      Р 1

B 2* ( x ) _ 9 2 (1 + 1" Г² + (1 - q 2 )(1 + — ) ^-1 - ₽ 2                    Р 2

в которых заданы положительные параметры 0- 1 - ^ 2 - Р 1 - р 2 - Р 1 - Р 2 и 0 <  9 1 <  1-0 <  q 2 <  1.

Рассмотрим пример со следующими значениями параметров:

« 1 _ 2 - « 2 _ 4 - Р 1 _ 5- Р 2 _ 3-

Р 1 ^{_ 2 -} Р 2 ^{_ 5-} У 1 ^{_ 2 -} У 2 ^_ 3.

Значения вероятностей положим равными q ₁ = 0-5- q 2 _ 0-7- Г 1 _ 1- Г 2 _ 0-5.

Таблица 1

Значения асимптотических средних числа заявок в источниках повторных вызовов

к1	к2
	0-2		0-4		0-6		0-8
	x 1	x 2	x 1	x 2	x 1	x 2	x 1	x 2
0-4	0-069	0-085	0-657	1-461	0-594	2-483
0-6	0-947	0-643	0-367	0-699	2-796	5-879
0-8	0-367	0-244	1-047	1-447
1-0	0-732	0-397	3-151	2-825
1-2	1-467	0-641
1-4	3-378	1-122
1-6

Таблица 2

Распределение вероятностей состояний прибора

Х 1	^ 2
	0,2			0,4			0,6			0,8
	R 0	R 1	R 2	R 0	R 1	R 2	R 0	R 1	R 2	R 0	R 1	R 2
0,4	0,60	0,19	0,21	0,37	0,19	0,44	0,10	0,21	0,69
0,6	0,50	0,27	0,23	0,26	0,28	0,46	0,05	0,36	0,59
0,8	0,40	0,37	0,23	0,16	0,40	0,44
1,0	0,31	0,46	0,23	0,08	0,53	0,39
1,2	0,22	0,56	0,22
1,4	0,14	0,68	0,18
1,6

В табл. 1 приведены значения асимптотических средних при различных значениях интенсивностей входящих потоков, в табл. 2 - распределение вероятностей состояний прибора. Незаполненные ячейки таблицы показывают те значения интенсивностей входящего потока, при которых стационарного режима в рассматриваемой системе не существует. Представляет интерес решение проблемы нахождения условий существования стационарного режима в рассматриваемой RQ-системе.

Заключение. В данной работе была исследована RQ-система с двумя входящими простейшими потоками, произвольным распределением времени обслуживания и вытеснением альтернативных заявок методом асимптотического анализа в предельном условии большой задержки. Для нее получены уравнения для нахождения среднего числа заявок в первом и втором источниках повторных вызовов, стационарного распределения состояний прибора. В качестве примера времени обслуживания были рассмотрены взвешенные суммы гамма- и экспоненциальных распределений. Для конкретных значений параметров системы получены среднее число заявок в первом и втором источниках повторных вызовов и распределение вероятностей состояний прибора. Модифицирован метод асимптотического анализа для исследования RQ-систем с двумя входящими потоками и вытеснением заявок.

Результаты выполненных исследований позволяют принимать управленческие решения для оптимизации функционирования космических сетей связи с целью предоставления более высокого приоритета для передачи важной или срочной информации.

Считаем целесообразным исследовать RQ-системы с неэкспоненциальной задержкой заявок в ИПВ, что является принципиальным, так как в научной литературе по системам с повторной очередью такие модели не рассматриваются в силу того, что используемые там методы не позволяют выполнить такие исследования. Применение в данной работе модификации метода асимптотического анализа позволяет надеяться на положительный результат.

Acknowledgments. The reported study was financially supported by RFBR according to the research project No. 16-31-00292 мол_а.