Исследование с помощью компьютерного моделирования влияния параметров кинетической характеристики трения на износ колес и рельсов

Введение. Износ колес и рельсов представляет собой очень важную и актуальную проблему, от которой во многом зависит эффективность работы железнодорожного транспорта. Ежегодные потери в масштабе железных дорог

Механика

России исчисляются миллиардами рублей [1]. Основным практическим методом борьбы с износом является лубрика-ция, направленная на снижение трения в системе «колесо — рельс». Однако таким образом решается лишь часть проблемы и далеко не всегда достигаются желаемые результаты. Большое значение имеет возможность прогнозирования износа и его изменений при осуществлении различных мероприятий. Такую возможность дает компьютерное моделирование взаимодействия железнодорожного экипажа и пути. Одним из хорошо известных и многократно проверенных инструментов такого моделирования является программный комплекс «Универсальный механизм» (далее «УМ»), разработанный в Брянском государственном техническом университете коллективом под руководством профессора Д. Ю. Погорелова. Описание возможностей УМ представлено в [2-5]. Комплекс, в частности, позволяет моделировать движение экипажа на прямых и кривых участках пути, вычислять различные величины, связанные с износом колес и рельсов.

Износ колес и рельсов сильно зависит от трения, на которое, в свою очередь, существенно влияют разнообразные количественные и качественные факторы. Большое значение имеет зависимость силы трения от скорости скольжения, поскольку качение колеса по рельсу часто сопровождается проскальзыванием. Исследование этой зависимости проводилось много лет. Еще в XIX веке на основе экспериментальных данных были получены эмпирические формулы, связывающие коэффициент трения и скорость скольжения. Такие исследования проводились и в ХХ веке, продолжаются они и в настоящее время. Различные формулы представлены в работах [6-8]. Между тем до сих пор нет ясности, насколько хорошо предлагаемые зависимости отражают реальные случаи, и как следует задавать различные их параметры в разных ситуациях с учетом многообразия действующих реальных факторов. В программном комплексе УМ используется формула, которая, как будет показано ниже, по сути является частным случаем известной формулы И. В. Крагельского — С. В. Щедрова [6]. В описании комплекса УМ [5] приводятся некоторые рекомендации по выбору параметров в зависимости от типа локомотива, влажности, наличия лубрикации. Представляет интерес изучение уровня чувствительности результатов компьютерного моделирования по износу к задаваемым параметрам. Кроме того, важно установить, каким образом изменение этих параметров в более широких пределах влияет на рассматриваемые процессы. На наш взгляд, такое исследование может, с одной стороны, помочь оценить точность компьютерного моделирования износа колес и рельсов, а с другой стороны — расширить понимание влияния различных факторов зависимости трения от скорости скольжения в целом. Последняя проблема имеет в трибологии большое значение, поскольку, как было установлено в многочисленных теоретических и экспериментальных исследованиях, такая зависимость является ключевой для возникновения фрикционных автоколебаний, которые играют значительную роль в различных областях техники [7]. Как показано в работах [8, 9], на эту зависимость большое влияние оказывают многочисленные взаимосвязанные количественные и качественные факторы. Попытка оценки этого влияния методами планирования эксперимента была сделана в [10]. В работах [11-13] были рассмотрены особенности трибологической информации и выработаны специальные методы ее анализа. Ниже представлена практическая реализация одного из предложенных там подходов для изучения кинетической характеристики трения в задачах, связанных с износом колес и рельсов. Результаты сопоставлялись как с уже упомянутыми отечественными работами [9, 10], так и с зарубежными исследованиями [14, 15], что позволило обосновать приводимые ниже выводы.

Анализ математических функций, выражающих кинетическую характеристику трения . Предварительное изучение функций, выражающих кинетическую характеристику трения, выполнялось простейшими методами математического анализа с применением программы MATHCAD.

Наиболее универсальной формулой кинетической характеристики трения является формула Крагельского [7]:

f ( v ) = ( a + bv ) e ^{- cv} + d                                                (1)

Здесь v — скорость скольжения, a , b , c , d — параметры кинетической характеристики. Физический смысл этих параметров связан сложными многофакторными зависимостями со свойствами материалов, поверхностей, конструкции узла трения, нагруженности и внешних условий. Качественный анализ этих зависимостей представлен в [6]. Количественное определение a , b , c , d из теоретических соображений пока не представляется возможным. В работе [7] кратко описана методика их экспериментального определения. Подробно различные подходы проанализированы в [8].

В программном комплексе УМ заложена более простая по сравнению с (1) формула:

g ( v ) = f > ( ( 1 - A ) e ^- B^v + A )                                                  (2)

Очевидно, что формула (2) является частным случаем формулы (1), т. е. функция f ( v ) переходит в g ( v ), если: d = f 0 A ; с = В ; a = f 0 ( 1 - A ) ; b =0.

Качественный физический смысл параметров A и B наглядно проявляется при поочередном приравнивании их к некоторым характерным значениям. Если A = 0, то получаем:

g ( v ) = f ) e ^- Bv .                                                          (2а)

Формула (2а) выражает монотонно убывающую функцию, и параметр B определяет скорость убывания. Величина B существенно зависит от температуры и давления.

Если А = 1, то g (v ) = f),                                                        (2b)

т. е. кинетическая характеристика вырождается в константу — коэффициент трения покоя.

Если B = 0, то при любом A приходим к случаю (2b), т. е. при равенстве параметра В нулю функция g ( v ) также вырождается в константу, являющуюся коэффициентом трения покоя. Если B находится в интервале ( -« ;)), то функция g ( v ) является возрастающей. Если параметр B находится в интервале (0; +^ ), то функция является убывающей.

Найдем первую и вторую производные функции g ( v ) по v . После преобразований получим:

g ' ( v ) = f ) ( A - 1 ) Be ^- B^v ,                                                  (3)

g ^v ) = f ) ( 1 - A ) B ² e ^{- Bv} .                                                  (4)

Согласно [7], в трибологических задачах (в частности, для взаимодействия колеса и рельса), как правило, 0 <  A < 1 и B > 0. Анализ формул (2)-(4) показывает, что такая ситуация соответствует монотонно убывающей функции g ( v ), и ее график является вогнутым.

Рассмотрим теперь функцию f тр ( A , B ), т. е. ту же кинетическую характеристику трения, задаваемую функцией g ( v ) по формуле (2), но при неизменной скорости и переменных параметрах А и В . С целью упрощения значение коэффициента трения f тр = g , получаемое по формуле (2), делится на константу f 0 (обозначим частное как f _ф2 :

f v2 = ^ = ( 1 - A ) --* + A.                                      (5)

J 0

При B = const :

- т²- = ( e ^{- Bv} - Ae ^{- Bv} + A ) ‘ = A (1 - e ^{- Bv} ),                                        (6)

аа mp2 > 0 при B > 0 и A > 0.

а а

При A = const :

^{d fmp2}- = ( e -^Bv ) '- A ( e -^Bv ) ‘ = - Be - ^Bv + ABe - ^Bv = Be - ^Bv ( A - 1),                             (7)

ab mp 2 > 0 при B > 0 и A > 1.

а в

5f mp 2

При А < 1, —— <  0, т. е. с ростом B f_mp2 уменьшается. а в

Методы, инструменты и результаты компьютерного моделирования. В качестве инструмента для проведения компьютерного моделирования использовался программный комплекс УМ — в частности, его модуль UM Loco, позволяющий моделировать движение железнодорожных экипажей. Был выбран компонент «колесная пара с 6 степенями свободы». Рассматривалось движение на прямых и кривых участках, причем брались правые кривые и соответственно вычислялся износ левых колес в колесной паре (по умолчанию в UM Loco рассматриваются правые кривые, поэтому износ обычно определяется на левых (набегающих) колесах). В данной работе использовалась упрощенная расчетная схема: одиночная колесная пара, катящаяся по рельсовому пути. В результате моделирования определялись количественные характеристики, непосредственно связанные с износом: мощность силы трения ( M_wear ), работа силы трения ( A wear ), удельная работа силы трения ( S wear ). Мощность силы трения при двухточечном контакте определяется как скалярное произведение силы крипа (трения) на гребне и скорости колес относительно рельса в точке контакта и рассчитывается по формуле:

Mwear =-F2хУ2x - F2уУ2у (Вт),(8)

Механика

Awear = 1 Mweardr (Дж),(9)

Swear = AwSear- (Дж/м),(10)

где S — пройденный путь.

Некоторые задававшиеся параметры моделирования представлены на рис. 1.

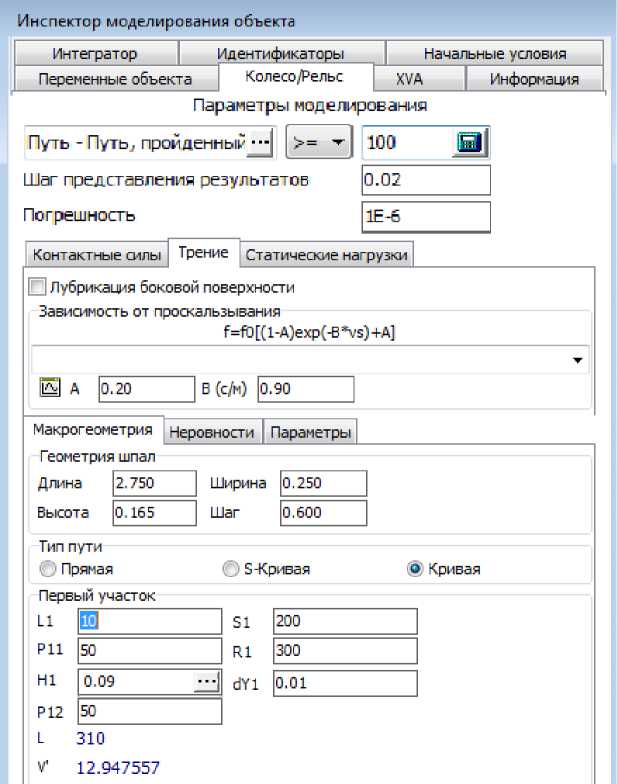
Рис. 1. Параметры моделирования изнашивания элементов системы «колесо — рельс»

Во вкладке программы «Колесо/Рельс — Трение» (рис. 1) задаются коэффициенты A и B , входящие в исследуемую зависимость силы трения от скорости скольжения. Здесь же приведена формула (2), используемая в программе.

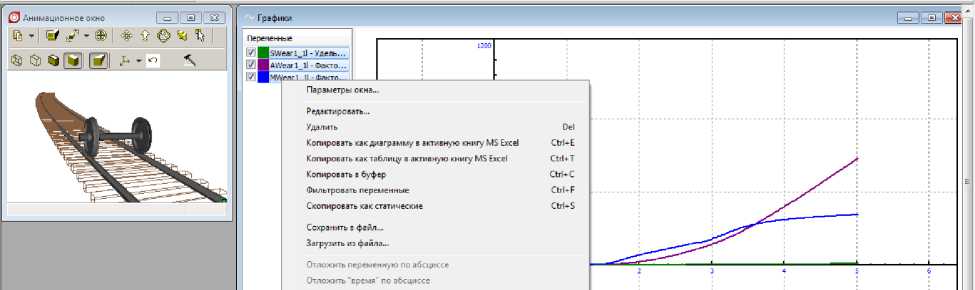
Рис. 2. Задание параметров зависимости трения от скорости

Результаты моделирования — значения S _wear , A _wear и M_wear , вычисленные по формулам (8)–(10) по найденным для данных моментов времени силовым и кинематическим переменным, можно перенести в MS Excel (фрагмент представлен на рис. 3). Столбец «Абсцисса» содержит модельное время в секундах, в других столбцах содержатся значения параметров в указанный момент времени.

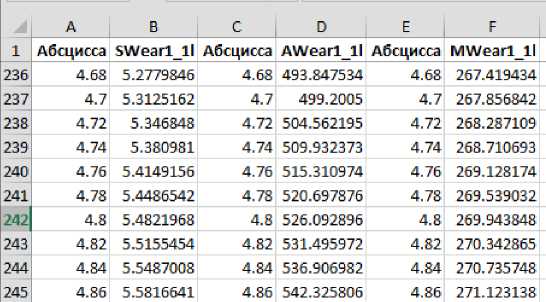
Рис. 3. Фрагмент результатов в окне MS Excel

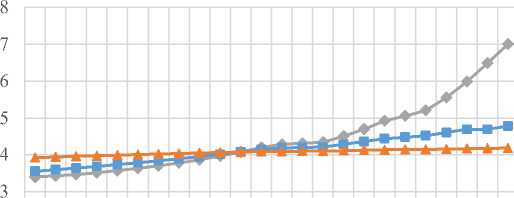
Компьютерное моделирование производилось многократно с различными значениями параметров A и B . На рис. 4 представлены графики, построенные на основании полученных результатов. По оси абсцисс указаны значения параметра B в диапазоне от –1 до 1, а по оси ординат — значения, связанные с износом исследуемых величин при указанных выбранных значениях параметра A .

S

A 0,1

A 0,5

A 0,9

–1 –0,8 –0,6 –0,4 –0,2 0 0,16 0,2 0,4 0,55 0,7 0,9 B

a)

A

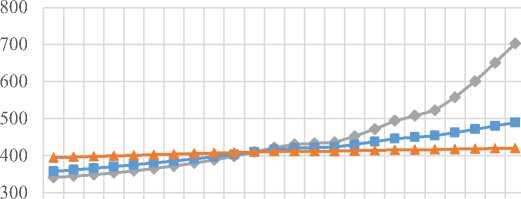
A 0,1

A 0,5

A 0,9

–1 –0,8 –0,6 –0,4 –0,2 0 0,16 0,2 0,4 0,55 0,7 0,9 B

б)

Механика

M

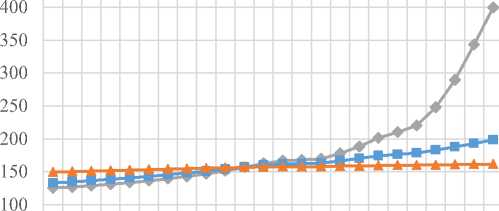
A 0,1

A 0,5

A 0,9

–1 –0,8 –0,6 –0,4 –0,2 0 0,16 0,2 0,4 0,55 0,7 0,9 B

в)

Рис. 4. Графики характеристик износа при некоторых значениях А

На рис. 5 представлены графики изменения тех же связанных с износом величин при некоторых различных значениях B . По оси абсцисс здесь отложены значения параметра A .

S

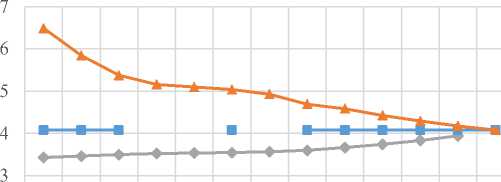
B –0,9

B 0

2                                                                        B 0,9

0,1 0,2 0,3 0,36 0,38 0,4 0,44 0,5 0,6 0,7 0,8 0,9   1

A

а)

A

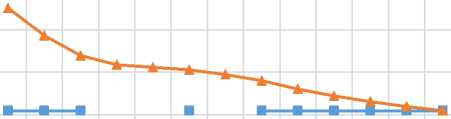
B –0,9

B 0

B 0,9

0,1 0,2 0,3 0,360,38 0,4 0,44 0,5 0,6 0,7 0,8 0,9 1

A

M

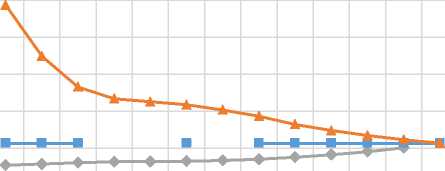
B –0,9

B 0

B 0,9

0,1 0,2 0,3 0,360,38 0,4 0,44 0,5 0,6 0,7 0,8 0,9 1

A

в)

Рис. 5. Графики характеристик износа при некоторых значениях В

Шаг и диапазоны изменения по параметрам А и В выбирались, исходя из намерений изучить чувствительность результатов к их изменению. Надо особо отметить, что ряд расчетов выполнялся с отрицательными значениями В в соответствии с возрастающей кинетической характеристикой трения. В реальном взаимодействии колеса и рельса такие случаи встречаются относительно редко, но они возможны при некоторых условиях смазывания и, кроме того, представляют теоретический интерес.

В табл. 1 представлены данные, полученные в результате анализа рис. 4, 5 и характеризующие разброс исследуемых параметров износа.

Таблица 1

Сводные показатели износа

	min	max	рост, %
wear	3,38	7,85	132,45
д wear	338,90	787,90	132,46
м wear	124,40	485,90	290,62

Как видно из табл. 1, разброс (разница между наименьшим и наибольшим значением) значительный по всем трем характеристикам, особенно чувствительной оказалась величина M _wear .

В табл. 2 содержатся значения коэффициентов А и В , приведенные непосредственно в программном комплексе УМ в качестве предлагаемых при компьютерном моделировании для некоторых типов локомотивов и при различном состоянии рельсов (влажные или сухие).

Таблица 2

Рекомендуемые в УМ значения коэффициентов А и В

Наименование	A	B
Локомотив, сухой рельс	0,4	0,6
Локомотив, влажный рельс	0,4	0,2
Локомотив SD45X, сухой рельс	0,44	0,6
Локомотив DB127, сухой рельс	0,38	0,7
Локомотив S252, сухой рельс	0,36	0,55
Локомотив SBB460, влажный рельс	0,5	0,16
Локомотив 12X, влажный рельс	0,4	0,4
Локомотив SD45X, влажный рельс	0,38	0,18

Механика

Анализ разброса результатов, собранных в табл. 3, относящихся к предлагаемым в УМ значениям А и В , показывает, что в этой области разница между наибольшим и наименьшим значениями характеристик износа не превышает 22 %. Надо отметить, что сама область является весьма узкой, и многие факторы, влияющие на кинетическую характеристику трения (температура окружающей среды, наличие и тип смазки, загрязнения и др.) здесь не учтены. Эти вопросы требуют дополнительного всестороннего исследования.

Таблица 3

Сводные показатели по предустановленным в программе параметрам

	min	max	рост, %
wear	4,14	4,80	16
А wear	415,07	481,94	16
M wear	159,40	194,18	22

По результатам компьютерного моделирования можно сделать также следующие выводы:

— при увеличении значения параметра B увеличиваются значения исследуемых характеристик износа S _wear , A _wear , M wear ;

— при увеличении значения коэффициента A уменьшаются значения исследуемых характеристик износа S _wear , A _wear , M wear , кроме случая при B = 0, когда эти характеристики не изменяются.

Отметим, что сопоставление последнего вывода со значениями найденных выше первых частных производных (при B > 0 и 0 < A < 1  тр2 > 0 и   тр2 < 0), говорит о том, что увеличение коэффициента трения может дА       дB сопровождаться уменьшением работы силы трения и износа.

Выводы. Результаты проведенного исследования позволяют сделать следующие выводы.

• 1.    В области значений параметров кинетической характеристики трения, соответствующих реальным ситуациям взаимодействия колеса и рельса, влияние их изменений на износ в общем случае является существенным, т. е. при компьютерном моделировании взаимодействия колеса и рельса надо учитывать зависимость коэффициента трения от скорости, если в задачу входит оценка износа.

• 2.    Как показывает компьютерное моделирование движения колесной пары по рельсовому пути, при падающей кинетической характеристике трения уменьшение коэффициента трения может сопровождаться увеличением характеристик износа.

• 3.    В трибодинамических системах значение коэффициента трения является функцией мгновенной скорости скольжения, которая изменяется во времени. Поэтому для компьютерного моделирования движения железнодорожных экипажей желательно использовать не кинетическую, а динамическую характеристику трения, которая может от нее существенно отличаться. Это требует проведения дополнительных теоретических и экспериментальных исследований.