Исследование самоорганизующихся процессов при формоизменении тонкостенных деталей импульсным магнитным полем

Самарский государственный аэрокосмический университет

Проведен анализ методов математического моделирования технологических процессов высокоскоростного деформирования материалов, характерных для магнитно-импульсной обработки. В зависимости от вида постановки смешанной задачи математической физики, описывающей процесс, рассмотрены численные методы решения и их сравнительная эффективность.

В современных условиях производства изделий авиационно-космической техники наиболее значимыми становятся задачи обеспечения показателей надежности при снижении весовых характеристик деталей и узлов и повышении экономической эффективности их изготовления. Одним из эффективных методов изготовления деталей является магнитно-импульсная штамповка.

В существующих технологиях изготовления деталей давлением импульсного магнитного поля (импульсного магнитного поля) одновременно присутствуют несколько факторов, обуславливающих оптимальные параметры протекания процесса пластической деформации металла, изменения микроструктуры материала детали и распределения деформаций по объему заготовки. В начальный момент нагружения заготовки давлением импульсного магнитного поля возникают электромеханические силы, характер которых определяется параметрами разрядной цепи “оборудование – инструмент – заготовка. Воздействие индуцированного высокочастотного тока на материал заготовки вызывает в поверхностном слое термоупругие напряжения, характер изменения которых представлен на рис. 1 [1].

Тепловая волна, распространяющаяся по объему деформируемого материала, одновременно повышает пластические характеристики металла и активное сопротивление разрядного контура. Последнее приводит к уменьшению коэффициента полезного действия процесса и сокращению времени деформацион- ного воздействия импульсного магнитного поля на заготовку. Электромагнитная волна, проникая через материал, в определенном диапазоне воздействия, приводит к уменьшению дефектов структуры и также к повышению пластичности.

Соударение заготовки с жесткой формообразующей оснасткой, вызывает появление на границе раздела в обоих материалах, упругих и пластических волн сжатия. Пластические волны вызывают пластическое деформирование материала заготовки и появления остаточных напряжений, на что расходуется большая часть ее кинетической энергии. Упругая волна сжатия в заготовке проходит до ее свободной поверхности и отражается упругой волной растяжения. Поскольку скорость движения пластической волны значительно ниже, упругая волна в материале накладывается на пластическую и снижает напряжения в ней, прекращая дальнейшее пластическое деформирование заготовки.

Рис. 1. Термоупругие напряжения в материале заготовки в зависимости от времени t, в периодах тока разряда Т

Повышение эффективности процессов магнитно-импульсной штамповки и улучшение эксплуатационных характеристик получаемых деталей возможно за счет управления и оптимизации параметров воздействующих факторов на заготовку. При выполнении поставленной задачи были проведены исследования практически одновременно протекающих процессов, сопутствующих деформационному, и проведен анализ их взаимного влияния на точностные и эксплуатационные характеристики заготовки.

В процессе деформирования заготовки определены следующие условно выделенные этапы:

• -    стадия интенсивного нагружения заготовки давлением импульсного магнитного поля и возникновения максимальных термоупругих напряжений на поверхности заготовки от индуцированного тока;

• -    стадия движения заготовки под действием кинетической энергии и прохождение тепловых и электромагнитных волн по объему материала заготовки;

• -    стадия удара заготовки о технологическую оснастку с наложением волновых эффектов при соударении;

• -    стадия разгрузки и формирования остаточных напряжений в объеме заготовки;

• -    стадия отскока заготовки от матрицы описываемая уравнением колебательного затухающего движения.

Расчет распределения токов и магнитного давления на поверхности заготовки для первой стадии проводится несколькими методами, например, с помощью векторного потенциала [2]. Однако, с учетом магнитной проницаемости материала заготовки полное решение интегродиффренциальных уравнений в частных производных является сложным даже численными методами. В предположении, что заготовка неподвижна, плотность электромагнитных сил, при определении полной силы, можно найти из выражения [2]

1 ² 5 L_u  5 M

2 5 x   5 x

где I – ток разряда, х – зазор между индуктором и заготовкой, L – индуктивность рабоче- го инструмента, М – взаимоиндуктивность индуктора и заготовки.

При расчете нагрева заготовки импульсом вихревого тока, вследствие его кратковременности, процесс можно считать адиабатическим. Количество тепла, выделенного в скин-слое (эффективном сечении) заготовки за время dt будет определяться следующей зависимостью:

^dQ = ^рГ- • ^{12 dt} ,             (2)

Sэф где ρ - удельное электросопротивление материала заготовки, Sэф – эффективное сечение, l – длина токового слоя заготовки, t – время воздействия.

На второй стадии с учетом движен(и3я) заготовки и электромагнитной волны в материале, определяющие уравнения могут быть представлены в следующем виде [3]

( X + 2 ц )	E	ρ E	—
	9 x	9 r 2	2 ц 9 x
(X + 2 ц )	9 2 U E	9 2 UF	9 T
		ρ E	— (3 ц + 2 ц ) a —-
	9x2	9 r 2	9 x
e 2 т	9 T	1 (	9 B ^ 2
X Я 2 9x	ρc v   1 d t	1 с гц 0 V	9 x J

(X + 2 ц) ’U - p 'U — (3ц + 2 ц)а ^ оx       о rox

9 ² T₂ χ ²

9x

-

TU pcv    - (3ц + 2 ц Wо

9t9x 9x

= (3 ц + 2 Ц)аТ₀

9 2UB 9 UT 9x 9x 9x 9t

где U_B – перемещение в электромагнитной волне, λ, µ – упругие постоянные Ламе, U_Т – перемещение в термоупругой волне, ρ – плотность, х – координата, t – время, С_v – удельная теплоемкость, Т – температура, α – коэффициент линейного расширения.

Выражение (3) описывает движение электромагнитной волны по объему заготовки. Выражение (4) описывает несвязанную тепловую волну Т₁, обусловленную Джоулевым нагревом, где U_T - перемещение в термоупругой волне.

В уравнение (5) вошли поправки физического процесса, связанные с действием одновременного возмущения от тепловой волны и электромагнитной, в начальный момент времени.

Решение для магнитной индукции дает исходную информацию для определения температуры.

В общем случае температурное поле должно удовлетворять условиям конвекции. Однако в качестве допущений принимаем, что конвекция на поверхности заготовки принята равной нулю.

Решение неоднородного уравнения, описывающего распределение температуры можно найти в следующем виде:

T ( x , t )

1 exp —- h α         4 αt

---------V I-------- /^П , (6) n (1 - 2ay² 2 a n (1 - ПУ2

где a - безразмерный параметр a =

σµ ₀ χ

PC v ’^X

- теплопроводность, о - удельная электрическая проводимость, п - безразмерный па-

2st (1 - 2 a ) раметр ^п =     /

τ ²

Температура на поверхности заготовки х=0 принимается постоянной, не зависящей от времени

Т

S

a 1 + + (1 - 2 a )> 2

--------7 ^n ---------7. (7) п (1 - 2 a /²   1 - (1 - 2 a /²

Выражение (7) позволяет пересчитать значение температуры в зависимости от величины магнитной индукции. Так например для алюминия ТS = 0,62 К при В0 = 1Вб/м2, для меди ТS = 0,40 К при В0 = 1Вб/м2.

Это приближение позволяет считать, что температура мгновенно повышается до значения Т_S , при воздействии ИМП, а затем поддерживается равной Т = Т₅ за счет тепла вызываемого рассеивающимся магнитным полем. Данное предположение подтверждается проведенными экспериментами.

Температурные волны, возбуждаемые Джоулевым нагревом вызывает ожидаемый скачек напряжения, связанный со скачком температуры на границе. Однако, в случае резкого повышения температуры на границе этот скачок при учете потерь на конвекцию превращается в плавный переходный процесс. В начале термические напряжения являются сжимающими, после отражения от границы появляются растягивающие напряжения.

Теоретическое исследование связанное с изучением эффекта пластичности можно разделить на два типа работ основанных на принципиально различных физических механизмах: “электронного ветра” и “электростимуляции” В них увеличение пластичности определяется импульсом электромагнитного поля, а определяющим параметром является вектор J . При этом амплитуда вектора плотности электрического тока велика | J r | <  10 9 A/м , а время мало (т ~ 10 -4 сек}.

В работах второго типа определяющим параметром является скаляр j² и его распределение в зоне деформации, время при этом не существенно. При этом плотность электрического тока | J ^ |< 10 9 A/м².

Феноменологический закон деформирования заготовки под действием эффекта пластичности от воздействия высокоэнергетического импульсного магнитного поля можно сформулировать с использованием следующих гипотез [3]:

dσ = (dε0 + α0θ )E - dσ, σ > σ0 dσ > 0, do = (d£0 + a06)E-E о> o0 do> 0.

Здесь ε₀ - упругая деформация; α, E, σ₀ – соответственно коэффициент линейного термического расширения, модуль упругости и предел текучести; θ - температура суммарного нагрева.

Приращение пластической составляющей напряжений определяется в следующем виде:

dσ_Р = Р(к)dW. (9)

Здесь к - параметр структурного состояния материала, для которого записано кинетическое уравнение dk = f(Wpq)dWp + f2(Wpq)dq, k > 0, (10) где dWp = σ dε, и функции P0, f1, f2 – задают- ся параметрами технологического процесса.

Уравнения (9) и (10) можно использовать как для одновременного, так и раздельного действия механического эффекта и энергетического воздействия.

В случае раздельного действия уравнения принимают следующий вид:

dсо Р = P(k)dW p , X o = X o (W⁰, q ); x ^ 0,

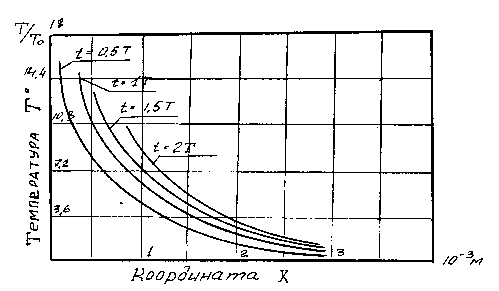
Рис. 2. Зависимость величины индукции магнитного поля от глубины проникновения в металл

где индекс 0 определяет состояние матери- ала перед повторным нагружением

β 2⁰

w p - w;

q ⁰

W⁰_p и W^-_p - работа пластической деформации к моменту повторного нагружения и работа пластической деформации без воздействия ИМП. Для материалов с упрочнением близким к линейному функционал определяется как

R (x) =

2m

° 0, ¹ +

2 m

σ ₀ χ ₀

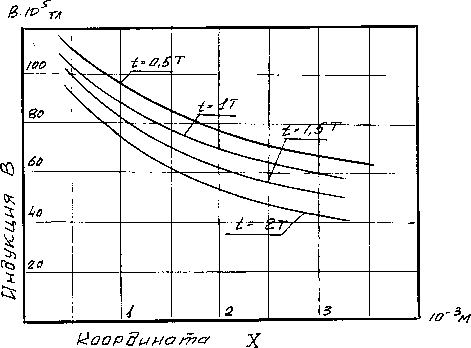
Рис. 3. Зависимость проникновения температурной волны в материал заготовки для различных моментов времени

Тогда закон деформирования (9) принимает следующий вид:

° p = ° 0

2 m

, ¹ + — ( X o ^{+ w} p ); ° >  ° 0 . (14) σ ₀

В случае одновременного действия соотношение для cc можно представить в виде dχ = dWp - β2dq,       (15)

где константа β₂ может определяться следующим образом:

_w ⁽ k ) - _w ⁽ н )

в2 = —---- q

Wp(k) и Wp(н) – работа пластической дефор- мации, соответствующая началу и концу процесса.

С учетом сказанного уравнение (14) примет вид:

° p = ° 0

2 m

1 + — (W p - в 2 q ), σ ₀

где m - параметр упрочнения материала при пластической деформации.

Результаты численного моделирования процессов теплового и электромагнитного воздействий на материал заготовки приведены на рис. 2 и 3, где показано проникновение магнитного поля и температурного поля в металл заготовки в одинаковые промежутки времени τ . Результаты расчета сделаны для алюминиевых сплавов.

На графиках рис. 2 и 3 время приведено

τ в безразмерных величинах т =   , где Т -

τ ₀          0

полупериод тока разряда в системе индуктор-заготовка.

Зависимости волн упругих напряжений, вызванных давлением вихревого тока, при проникновении магнитного поля в материал заготовки, приведены на рис. 4.

Волны, обусловленные произведением векторов тока _I и индукции магнитного поля

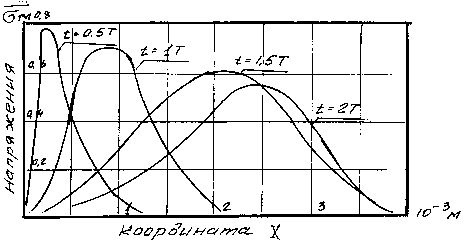
Рис. 4. Зависимость волны упругих напряжений от различных моментов времени

_B , дают объемную силу _I × _B , проник а ющую в металл со скоростью С. Напряжения ограничиваются величиной B ₀² / 2 µ ₀ . Волны, обусловленные _I × _B являются волнами сжатия.

Анализ результатов численных исследований показывает, что повышение температуры на поверхности заготовки от вихревого тока может вызвать напряжения больше, чем от магнитного давления – B ₀ ² I 2 µ . Однако они затухают при проникновении термоупругой волны в материал заготовки. Волны, вызванные магнитным давлением, распространяются в твердых телах с малым затуханием.

Волновые эффекты, возникающие при ударе заготовки о технологическую оснастку приводят к напряжениям, которые определяются отношением динамических жесткостей материалов заготовки и матрицы и скоростью их соударения [4].

Для описания протекающих в деформируемых трубчатых заготовках механических процессов использован вариационный принцип Гамильтона-Остроградского, который в общем виде может быть описан следующим соотношением [1]:

δW_K = δW_n + δA_y + δA_S, (17) где δW _к , δW _n , δA_y , δA_S – вариации К-го состояния кинетической, потенциальной энергии, работы объёмных и поверхностных сил соответственно.

При решении нелинейной задачи механики деформируемой среды используем итерационный метод. Вариационное уравнение последовательно преобразуется в метрике К_i

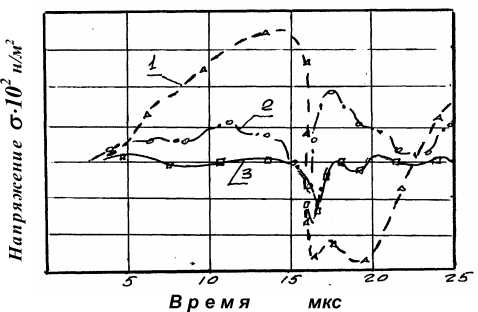
Рис. 5. Распределение текущих напряжений в начальныймомент деформирования: 1 – радиальные, 2 – меридиальные, 3 – тангенциальные состояния соответствующего положению среды на произвольной Кi итерации. Для этого используем соотношения между векторами различной ковариантности и правило преобразования оператора Гамильтона.

При численной реализации вариационного уравнения Гамильтона-Остроградс-кого граничные условия задаются для фиксированного момента времени. Для записи граничных условий рассмотрены все стадии деформирования.

Для численных исследований используется метод конечных элементов.

При определении параметров напряжённо-деформированного состояния расчётной модели на временном шаге dt для каждого конечного элемента всех блокфрагментов последовательно вычисляются все характеристики деформируемой среды.

Метрические характеристики конечных элементов (КЭ) пересчитываются на каждом шаге, что в целом позволяет учесть геометрическую нелинейность задачи. Учет физической нелинейности производится путем корректировки на каждом шаге девиаторной части полных напряжений.

Решение в аналитическом виде приведенных задач влияния факторов импульсного магнитного поля на материал деформируемой заготовки является весьма сложным. Для достижения поставленной цели по разработке методов проектирования технологических процессов на формирование напряженно-деформированного состояния материала заготовки каждое воздействие моделировалось неза- висимо от других. Интегральная характеристика получена наложением картин текущих и остаточных напряжений времени рис. 5.

Математическое моделирование технологий изготовления деталей давлением импульсного магнитного поля позволило выбрать оптимальные параметры технологических процессов и прогнозировать свойства изготовляемых деталей и обосновать новые технические решения по дальнейшему расширению возможностей метода.