Исследование сценария перехода к хаосу в динамической системе с особой окружностью на фазовой плоскости

Астахова. В [6] впервые предложена автономная точечная модель, описывающая бифуркацию удвоения тора в двухмодовом лазере с насыщающимся фильтром.

В настоящей работе исследованы бифуркации и сценарий перехода к хаосу через удвоение тора в моделирующей генерацию лазера с отстройкой частоты динамической системе, имеющей стационарное состояние в виде особой кривой.

Рассмотрим систему уравнений Максвелла - Блоха с адиабатически исключенной поляризацией и отстройкой частоты:

дЕ д 2 E v ( N iI dt    дх2   2 V1+ А2о

- 1 1 ( Е - iE А о ) ,

d.

un d t

-

( А

N 1 +----г

1 + л 2

V    ^{1 + А} о 7

.

Предполагается также, что генерация происходит на одной продольной моде резонатора Фабри-Перо. Здесь E – медленно меняющаяся амплитуда поля в широкоапертурном лазере в одномерном (планарном) приближении, обез-размеренная на величину Es , Es — амплитуда поля насыщения в активной среде, N — g I gt ;g, gt – коэффициенты усиления активной среды на центральной частоте лазерного перехода и потери, усредненные по длине резонатора ; безразмерное время t и координата x связаны с размерными величинами td и xd, как t — td I Tt , x — xd (2 k I Tc )112 , k – волновое число; c – скорость света; Ti – время релаксации населенности уровней активной среды; v — cTigt -коэффициент, определяющий отношение времени релаксации населенности активной среды ко времени жизни фотонов в резонаторе ; А0 — (^o — ю)TP — отстройка частоты генерации от центра линии усиления АС, обезразмеренная на полуширину линии усиления ; Tp – время релаксации поляризации; J = |E2, Nun = gun Igt, gun – ненасыщенный коэффициент усиления на частоте too.

Запишем исходную систему уравнений в автомодельной системе координат ( § = t — в x , где w = 1I в - скорость волны, распространяющейся в поперечном к оси резонатора направлении) и получим систему обыкновенных дифференциальных уравнений:

dE 1 = y d§     ’ dE 2 _

Z , d§

При в = вы f на фазовой плоскости ( J , N ) происходит бифуркация Андронова-Хопфа и рождение предельного цикла бесконечно малой амплитуды. В результате этой бифуркации рождается семейство периодических волн интенсивности малой амплитуды J ( § ) , бегущих поперёк апертуры со скоростью w_cr . В точке бифуркации значение частоты модуляции интенсивности и коэффициента усиления соответствует

® bif

Nun 2

+ A oVIst IA ol

dN — N d §

un

^^^^^^e

N

1 + E ² + E 2

1 + A o²

,

dY d^

в ²

" f

² 1 1 + A o²

— 1 ( E 2

^— A o ^E 1 ^{) —} Z

dZ 1

d § = в ²

v f N

2 l T +A^

— 1 ( E 1 7

+ A o E 2 ) — Y

Нетривиальный стационарный режим генерации с интенсивностью J st соответствует осо бой окружности ( E s_t + E 2 st = ^Js, = N _un ^— 1 ^—^ , N _st = 1 + A _o ² , Y_st = o , Z _st = o ) в фазовом объеме. Отметим, что подобная особая окружность на фазой плоскости всегда возникает при описании стационарной генерации. В [7] показано, что стационарное состояние ( J_st , N_st ) становится неустойчивым при

в > вbif =

( 1 + 1, ) A o

( 1 + 1 „ ) ² +A o ² v I„

Ist

Jst

В пространстве ( E 1 , E ₂, N ) точке бифуркации соответствует структурно неустойчивый тор, бесконечно малого сечения. При в >  в 1^ тор “разбухает”, подобно надуваемой шине. При этом фазовая точка движется с частотой ® ~ ® bif вокруг особой кривой и с частотой Q <<<  to bif вдоль особой кривой (рис.1а). Такой динамический режим соответствует квазипери-одическим волнам оптического поля E 1 ( § ), E ₂ ( § ) . Ранее была известна и широко описана в литературе бифуркация периодического режима частоты Ю | в квазипериодический с несоизмеримыми частотами ® 1 , to 2 , причём to 2 < to 1. В фазовом пространстве при этом предельный цикл сменяется устойчивым двумерным тором. Фазовые траектории раскручиваются в направлении прежнего предельного цикла и медленно накручиваются на тор (рис. 1б).

Система (2) описывает бифуркацию нового типа : непростое стационарное состояние в виде особой замкнутой кривой “структурно неустойчивый трёхмерный тор – устойчивый двумерный тор”. Как показано на рис. 2а, сигнатура спектра Ляпуновских характеристических показателей X i меняется при этой бифуркации (точка А) как

o----^ ooo — ^ oo---

1+ A

—, A _o <  o . o

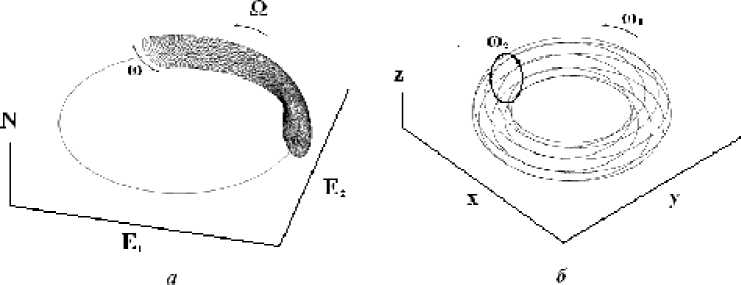
Рис. 1. Бифуркация рождения двумерного тора: а – из особой кривой; б – из предельного цикла.

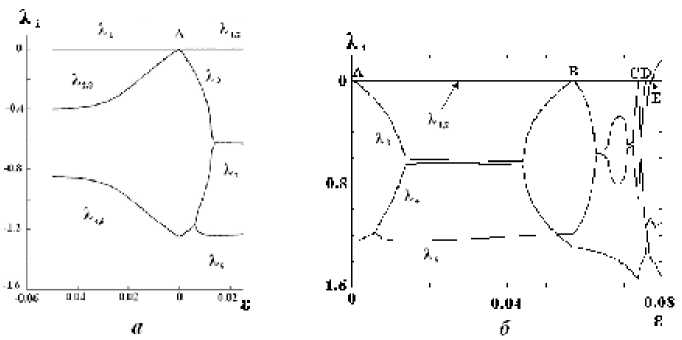
Рис. 2. Спектр Ляпуновских характеристических показателей

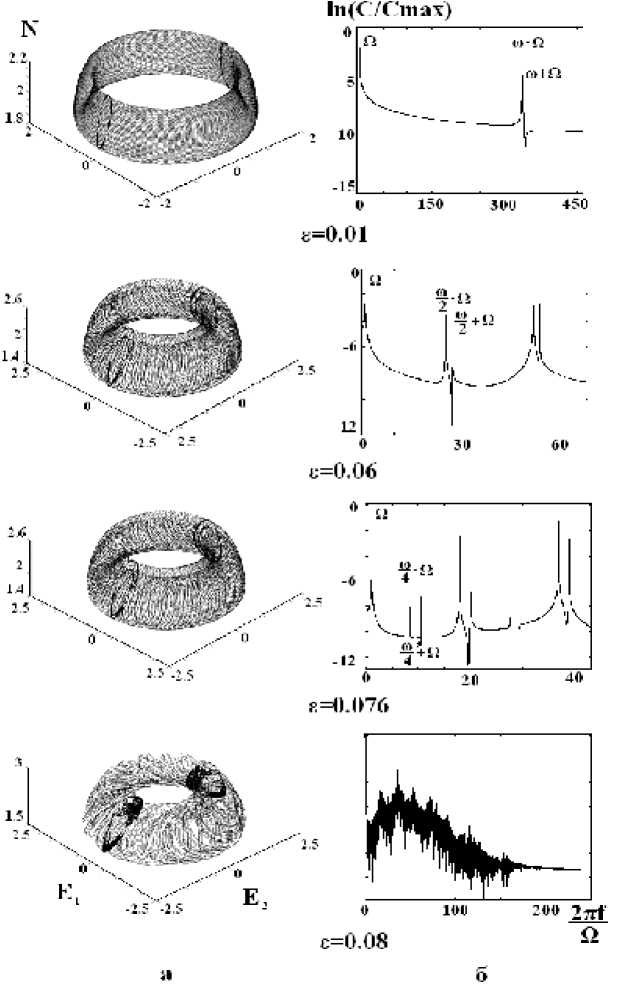
Рис. 3. Последовательность бифуркаций удвоения тора при изменении параметра ε в пространстве ( E1, E2 , N ):

а – фазовый объём, б – спектр колебаний E ₁ ;

C – мощность спектра, C _max – максимальное значение мощности, f – линейная частота

Направление фазовых траекторий на торе тоже другое (рис. 1a.)

На рис. 3, 4 показаны последующие бифуркации тора при изменении управляющего параметра Б = ^{( e} - P bif ) / P bif .

Для наглядности использовались проекции исходного пятимерного пространства в два разных трёхмерные фазовые подпространства. Анализ полученных фазовых портретов и спектров, а также построенных отображений Пуанкаре, позволяет утверждать, что при увеличении управляющего параметра происходит каскад бифуркаций удвоения периода тора, приводящий к хаотическому режиму. О наступлении хаотического режима свидетельствует сплошной спектр, плотное заполне- ние “бабочки” в сечении Пуанкаре, а также карта характеристических Ляпуновских показателей (рис.2). Из. рис. 2 следует, что в точках бифуркаций А, В, С и D рождается структурно неустойчивый трехмерный тор, который, разрушаясь, порождает устойчивый удвоенный двумерный тор. В точке Е старший показатель Ляпунова становится положительным, а сумма показателей Ляпунова по - прежнему отрицательной. Это как раз свидетельствует о возникновении странного аттрактора и реализации режима динамического хаоса.

Таким образом, показано, что в динамической системе с замкнутой особой кривой возможно образование двумерного тора и переход к хаосу через каскад бифуркаций удвоения периода тора.

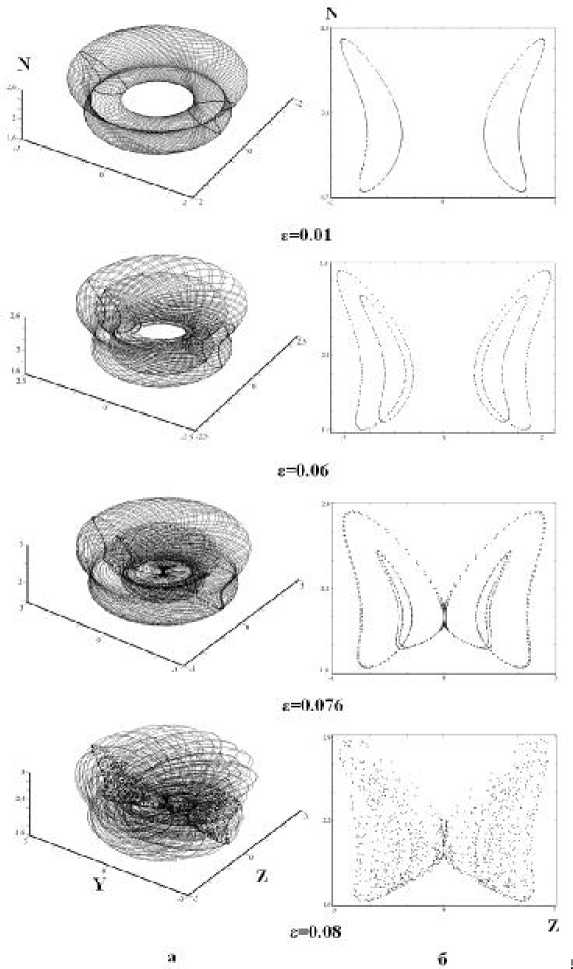
Рис. 4. Последовательность бифуркаций удвоения тора при изменении параметра б в пространстве ( Y , Z , N ): а – фазовый объём, б – сечение Пуанкаре

Работа поддержана Федеральной целевой программой “Научные и научно-педагогические кадры инновационной России” на 2009 – 2013 годы, НК-387 (23), аналитической целевой программой “Развитие научного потенциала высшей школы” (2009 – 2010 гг.), проект 2.1.1/309, НОЦ 14.