Исследование систем молниезащит объектов в виде ветроэнергетических установок на основе математического моделирования

моделирования. Один из обзоров этих методов и эмпирических подходов с учётом их недостатков приведен в [7].

Цель работы: представление особенностей метода математического моделирования для исследования электроэнергетических объектов c СМЗ, находящихся между грозовым облаком и поверхностью земли, на основе расчёта потока напряжённости электростатического поля (силовых линий электростатического поля в виде семейства уравнений µ i = const с равным шагом) и учёта соотношений размеров исследуемого объекта с СМЗ стержневого типа.

Численные расчёты с распределенными молниеприемниками в виде башен с цилиндрическими стержнями относительно стартовой площадки, рассматривались в [8, 9]. За основу схемы моделирования принята типовая схема в виде некоторого прямоугольника, по углам которого установлены молниеприёмники. В центральной части схемы находятся технологическая мачта с ракетой-носителем, как представлено в обзоре [10]. Расчётная область расположена в плоскости, проходящей по диагонали исследуемой схемы от одного молниеприемника к другому через мачту с ракетой-носителем. В расчётах определяются атмосферные электростатические поля СМЗ стартовой площадки. Внешняя краевая задача сведена к внутренней.

В [2] на примере расчёта трёхмерной задачи показано, что внешнюю краевую задачу с минимальными погрешностями можно свести к внутренней в отличие от существующих подходов [11].

В [12] решается внутренняя краевая задача, и исследуются молниеприёмники, находящиеся в центральной части ограниченной трёхмерной области, например, в виде куба. При этом считается, что верхняя горизонтальная плоскость этой области является облаком, а нижняя - поверхностью земли. Сравнительный анализ результатов решения внешней краевой задачи [2] с данными [12] показывает об имеющейся дополнительной возможности сведения внешней краевой задачи к внутренней с относительно минимальными погрешностями, что также применяется в работе.

Постановка задачи. Определяются электростатические поля ветроэнергетической установки (ВЭУ) с учётом данных [13, 14]. За основу принята схема моделирования ВЭУ с лопастями ротора длиной L ₀=60 м [14]. Однако для исследуемой области С ( x , у ) в отличие от расчёта трёхмерной задачи в [14], выбрана двумерная задача, причем одна из лопастей находится по оси в нижней части башни, а остальные две - в верхней части области С ( x , у ). Схема моделирования С ( x , у ) с ВЭУ, показана на рис. 1. В схеме моделирования учитывается подход [8, 9] с возможностью сведения внешней краевой задачи к внутренней путём расположения электроэнергетического объекта между верхней и нижней границами С ( x , у ), а на боковых границах С ( x , у ) задаётся условие вида Е_п =0 ( Е_п - напряжённость электростатического поля по нормали к этим границам) [2]. Считается, что границы С ( x , у ) следующие: G ₁ - поверхность земли; G ₅ - башня ВЭУ; G ₆ - лопасть ротора; G 3 - некоторая эквипотенциальная поверхность у i = const, которая вводится в расчётную область вместо границы облака на основе [8, 9]). Согласно данным [8, 9] для замены границы облака некоторой эквипо-тенциалью у _i =const достаточно, чтобы у _i =const находилась на уровне порядка 3-х высот башни ВЭУ. Тогда боковые границы G ₂ и G ₆ искусственно ограничивают С ( x , у ) и находятся на равных расстояниях от башни ВЭУ. С учётом симметрии электроэнергетического объекта, вместо G ₆ в водится граница G ₄, являющаяся также осью симметрии области С ( x , у ).

Распределение электрической функции потока ц определяется из уравнения Лапласа, представленного относительно ц в виде:

• □    д ц /д x ² + д 'ц /д у ²=0; ( x , у ) е С ( x , у ), (1)

т.е. (1) - уравнение эллиптического типа относительно µ. На основе расчёта поля µ определяется семейство силовых линий с заданным шагом. Граничные условия задачи c учётом рис. 1 следующие (для ВЭУ без СМЗ):

• -    на границах G ₁, G ₃ области С ( x , у ):

дц/дn=0, (x,у) е G 1, G3;(2)

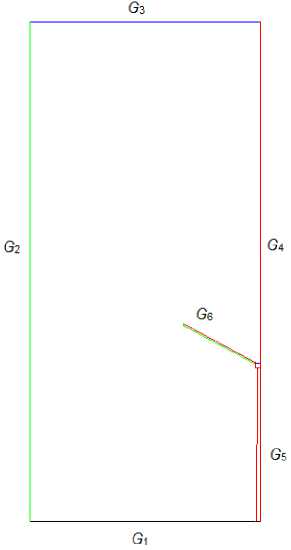
Рис. 1. Схема моделирования области С ( x , у ) с ВЭУ

- на границах ВЭУ G 5 и G 6 :

дц/дn = 0, (x,у) е G5, G6;(3)

• -    на границе G ₂ области С ( x , у ):

ц(x,у)=ц0, (x,у) е G2;(4)

• -    на границе G ₄ области С ( x , у ):

ц(x,у) = 0, (x,у) е G4;(5)

где С ( x , у ) - исследуемая область, ограниченная G 1 - G ₆; ц₀ = const.

К граничным условиям задачи для ВЭУ с СМЗ стержневого типа (стержень устанавливается на гондоле по G ₄) вместо уравнения (5) добавляются следующие:

• -    на одной части G ₄ с СМЗ (при изменении длины стержня), т.е. на границе G ₄₁:

дц/д n = 0, ( x , у ) е G ₄₁;                  (6)

• -    на оставшейся части границы G 4 выше СМЗ, т.е. на границе G 42 :

ц( x , у ) = 0, ( x , у ) е G 42 .                   (7)

Следовательно, для ВЭУ без СМЗ применяются уравнение (1) с граничными условиями (2) - (5), а для ВЭУ с СМЗ стержневого типа соответственно уравнение (1) с граничными условиями (2) - (4) и (6), (7).

Результаты численных расчётов. В [14] представлены инновационные технические решения и их исследования для ВЭУ с различными типами СМЗ. Для качественного сравнения данных [14] с результатами расчётов по предлагаемому методу математического моделирования выбираем ВЭУ с СМЗ стержневого типа длиной L i=100 м, что существенно превышает применяемые стержни на гондоле ВЭУ, а также длину лопастей ротора ВЭУ. При численных расчётах поля функции потока ц используется разностная сетка для уравнения (1) (сетка является регулярной прямоугольной (Ax=Ay=A)) [15]. При численных расчетах задачи не учитываются размеры в сечениях лопастей ротора ВЭУ (см. рис. 1) и в сечениях СЗМ стержневого типа, так как они пренебрежимо малы по сравнению с шагом A сетки по x, у (например, только длина лопастей в роторе ВЭУ 60 м).

Для дискретных областей С/x , у ) при решениях задач для ВЭУ c СМЗ и без СМЗ во внутренних узлах сетки выполняется условие сходимости итерационного метода Гаусса-Зейделя. В узлах области С_d ( x , у ) функция потока ц ij• рассчитывается с помощью численного метода, например, ускоренного метода Либмана [16] (в отечественной литературе также называется методом верхней релаксации) на основе уравнения Лапласа в конечно-разностных аппроксимациях по аналогии, как в задачах [8, 9, 17, 18]. На границах G i дискретной С^x , у ) рассчитываются функции потока ц в узлах ( i,j ) с учетом конечно-разностных аппроксимаций для соответствующих условий: (2) - (5) или (2) - (4) и (6), (7) с учётом решаемой задачи.

Постановка задачи в дискретной области С^x , у ) для ВЭУ без СМЗ . Для этой краевой задачи с учётом уравнения Лапласа и граничных условий (2)-(5) требуемые уравнения в операторной форме для определения функции потока ц в узлах ( i,j ) дискретной области C d ( x , у ) следующие:

W xx Ц ij + W yy Ц ij = 0,⁽ X , У, ) ^е C d ^{( x}, У );

W n ц j = 0, ( X i , y j ) е G 1 , G 3 , G 5 , G 6 ;

Ц j =Ц о , ⁽ X , y j ) ^е G 2 ;

^ц j = 0, ( X i , У J ) е G 4 .

Здесь W xx =d /д x ², W yy =0² /д у ², W_zz=d 2 /д z ², W „ =d /д n - производные функции ц, которые представляются конечно-разностными аппроксимациями. Область C d ( x , у ) является дискретной с регулярной прямоугольной сеткой. Для аппроксимации различного вида границ применяется известный алгоритм Брезенхэма.

Результаты расчёта атмосферного электростатического поля в области С ( x , у ) с ВЭУ в виде силовых линий µ i =const с равным их шагом Δµ

W h V ⁽ h ) ^^

без применения СМЗ показаны на рис. 2 а ; с применения СМЗ стержневого типа показаны на рис. 2 б.

Рис. 2. Результаты численных расчётов атмосферного электростатического поля в С ( x , у ): а -при отсутствии СМЗ; б - с СМЗ стержневого типа

На основе полученных результатов рассмотрим особенности исследования ВЭУ с СМЗ при их нахождении между поверхностью земли и некоторой эквипотенциалью у i =const, введённой в расчётную область вместо облака [8, 9, 17, 18]. Для этого определим плотность распределения х■ силовых линий атмосферного электростатического поля в исследуемой области С ( x , у ) с ВЭУ для задач:

• -    без применения СМЗ относительно: 1) ВЭУ; 2) поверхности земли (ПЗ);

• -    с применением СМЗ стержневого типа относительно: 1) ВЭУ; 2) ПЗ; 3) СМЗ.

Результаты численных расчётов для этих задач сведены в табл. 1.

Таблица 1. Плотность распределения линий ц i =const в С ( x,y ), т.е. с учётом их количества ( n i ), приходящихся на исследуемые элементы С ( x,y )

Элементы С ( x -У )	ВЭУ без СМЗ		ВЭУ c СМЗ
	n i	X i (%)	n i	X i (%)
ВЭУ	28,5	71,25	3,5	8,75
ПЗ	11,5	28,75	3,5	8,75
СМЗ	-	-	33	82,5

Сравнительный анализ данных на рис 2 и в табл. 1 показывает, что в условиях применения СМЗ стержневого типа для ВЭУ плотность распределения χ i уменьшается на электроэнергетическом объекте приблизительно на 60% по сравнению с ВЭУ без СМЗ. Полученные результаты качественно совпадают с данными [14]. Для выявления оптимальной высоты стержня необходимо проводить дальнейшие исследования. Например, если стержень будет равен 30 м (т.е. 0,5 лопасти), то плотность распределения линий µ i =const уменьшится в пределах 45% по сравнению с ВЭУ без СМЗ. В отличие от [14] также установлено, что на поверхности земли вблизи ВЭУ наблюдается изменение плотности распределения χ i по сравнению с ВЭУ без СМЗ.

Аналогичные результаты получены при расчётах атмосферных электростатических полей СМЗ стартовой площадки с учётом топологии СМЗ относительно объекта защиты [8, 9]. Они показали, что при уменьшении дистанции L i между СМЗ и объектом защиты плотность распределения χ i существенно уменьшается на объекте защиты, но при этом увеличивается на СМЗ. Это подтверждается данными [19] о СМЗ стержневого типа для ракеты-носителя типа « Антарес » . До момента старта « Антарес » стержневые молниеприёмники на стартовой площадке находятся на минимальной дистанции от объекта защиты [19]. Однако при старте ракеты-носителя стержневые молниеприёмники перемещаются на некоторое расстояние для исключения воздействия высокоскоростных и высокотемпературных газовых потоков на элементы СМЗ. В этом случае топология СМЗ относительно объекта защиты соответствует типовой схеме [10].

В [8, 9] также установлено изменение плотности распределения χ i на поверхности земли при изменении дистанции L i между СМЗ и объектом защиты. Полученные результаты теоретических исследований этой работы и [8, 9] дают возможность объяснять известные данные [20] относительно удара молнии в нижнюю часть стартовой площадки с шаттлом, а не в СМЗ с высотой существенно превышающей объект защиты.

На основе полученных результатов установлено, что имеется возможность исследовать особенности применения стержневого молние-приёмника, устанавливаемого на гондоле ВЭУ, т.е. по границе G4. С инженерной точки зрения изготовление такого стержня затруднительно, как отмечено в [14]. Однако проблема может быть решена с применением новых технологий и материалов для этого типа молниеприёмника. В этом случае также упрощается задача заземления этого стержня.

Выводы:

• 1.    Установлена возможность применения для ВЭУ с СМЗ или без этой системы защиты метода математического моделирования на основе расчёта силовых линий электростатического поля в виде уравнений µ i const с равным шагом. Это позволяет исследовать как особенности технологий молниезащиты, так и определять рациональные параметры этих схем.

• 2.    Анализ технических решений основан на расчёте плотности распределения силовых линий µ i =const в исследуемой области, т.е. на определении их количества, приходящихся на элементы в этой области.

• 3.    Предлагаемый метод позволяет анализировать, как особенности атмосферного электростатического поля вблизи остроконечных вершин, так и исследовать эти поля на поверхности земли относительно объектов защиты. С теоретической точки зрения это позволяет объяснять существующие данные об ударах молний не в верхние части СМЗ.