Исследование систем поллинга с использованием имитационного моделирования

Система, поллинга. - это система, массового обслуживания, которая имеет общий сервер (или несколько серверов) для всех очередей, сервер по определенному правилу обходит очереди и обслуживает заявки, которые поступают в систему и накапливаются в ее очередях. Такие системы находят применение в широкополосных беспроводных сетях с централизованным управлением, PCF (Point Coordination Function) под управлением протоколов IEEE 802.11 или 802.16.

Правило посещения сервером каждой очереди называется порядком поллинга (или порядком опроса). Предполагаем, что система поллинга имеет п очередей, очереди занумерованы от 1 до п. Будем обозначать через Qi очередь с номером г. Опишем некоторые виды порядка, опроса:

• 1.    Циклический поллинг: сервер посещает все очереди в порядке

• 2.    Адаптивный динамический поллинг: в первом цикле сервер опрашивает очереди от 1 до п, в следующем цикле он пропускает (не посещает) те очереди, которые были пусты в момент их опроса в первом цикле. Пропущенные очереди далее будут опрашиваться сервером в следующем цикле, и процедура опроса повторяется таким образом, что пустые на момент их опроса очереди не участвуют в следующем цикле опроса. Если же все очереди в цикле опрашивались и оказались пусты, сервер может брать некоторое время на отдых и далее начать опрос всех очередей по циклу как описано выше.

• 3.    Упорядоченный адаптивный динамический поллинг: в первом цикле всем очередям присваивается ранг т = 0, г = 1 .. .п. Если при опросе очереди г она пуста, то ее ранг уменьшается на 1, т.е. Тг = —1. В противном случае ранг этой очереди увеличивается на 1, т.е. тг = 1. В следующем цикле сервер опрашивает очереди по порядку убывания их рангов. Если несколько очередей имеют одинаковый ранг, то сервер опрашивает эти очереди в порядке возрастания их номеров. Минимальное значение ранга равно — 1, и если ранг очереди достиг этого значения, то в следующем цикле сервер пропускает эту очередь и увеличивает ранг на 1.

Q 1 ,Q 2 ,...,Q h ,Q 1 ,Q 2 ,...,Qn,...

(с) Буй Д. Т., Семёнова О. В., 2018

Дисциплиной обслуживания очереди называется число заявок, которое обслуживает сервер за одно посещение очереди. В данной работе рассмотренны две популярные дисциплины:

• 1.    Исчерпывающая дисциплина: сервер обслуживает заявки до тех пор, пока очередь не опустеет.

• 2.    Шлюзовая дисциплина: сервер обслуживает лишь те заявки, которые находились в очереди в момент ее опроса.

2.    Имитационное моделирование системы поллинга

Для моделирования систем поллинга с адаптивным опросом используем OMNeT++ Discrete Event Simulator. В данной работе рассмотрена система с одним сервером и п = 6 очередями типа M/M/1 (см рис. 1). Время обслуживания заявок не зависит от номера очереди и распределено экспоненциально с парамером 10 000. Предполагаем, что потоки заявок в очереди простейшие. Интенсивности потоков заявок в первые три очереди эквивалентны и равны 1000, а интенсивность поступления заявок в три следующие очереди (с номерами 4-6) изменяется от 1 до 1500. Время переключения сервера между очередями распределено экспоненциально с параметром 1000.

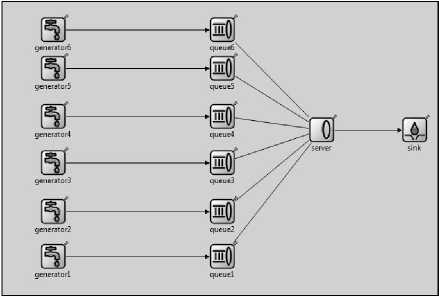
Рис. 1. Модель поллинга. для шести очередей

Результаты имитационного моделирования показывают, что время пребывания заявок в системе при исчерпывающей дисциплине меньше чем время пребывания при шлюзовой дисциплине для всех трёх видов порядка, опроса, (см рис. 2, 3 и 4). Когда, интенсивность входного потока, меняется от 1 до 1500, доля пропущенных циклов в системе с адаптивным динамическим поллингом и с упорядоченным адаптивным динамическим поллингом меняется от 0,49 до 0.

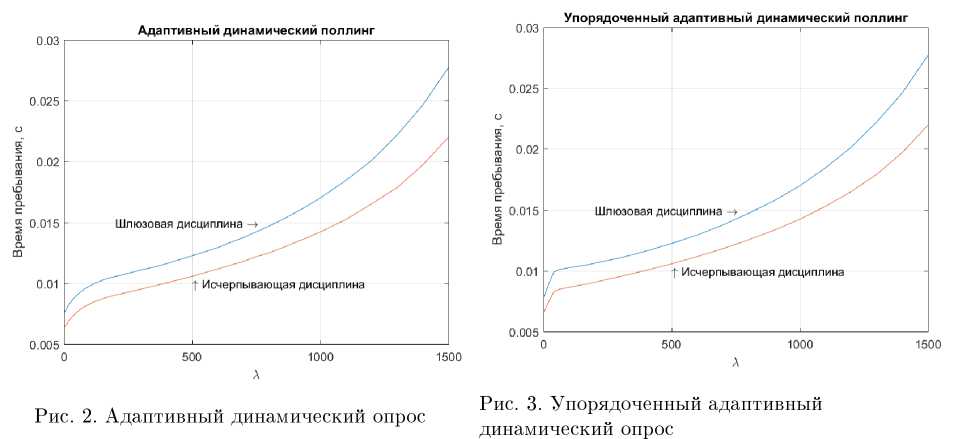
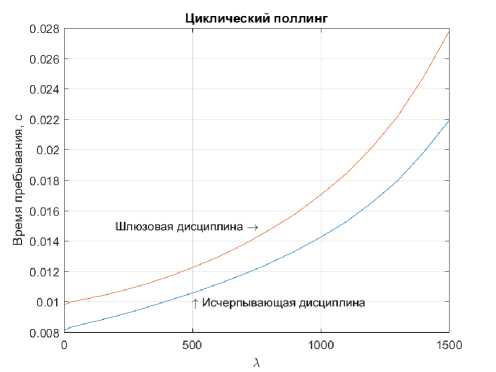
Рис. 4. Циклический опрос

Когда интенсивность входного потока в последних трех очередях меняется от 1 до 1500, загрузка всей системы меняется от 0.3 до 0.75, при этом доля пропущенных циклов для каждой из очередей меняется от 0.49 до нуля при адаптивном динамическом и упорядоченном адаптивном динамическом опросе. При загрузке системы больше 0.75 программа имитационного моделирования не позволяет получить результаты расчетов за разумное время, при этом заметим, что при интенсивности входных потоков у последних трех очередей больше 300, среднее время пребывания для всех видов опроса практически совпадает. Этот результат прямо следует из определения адаптивного динамического опроса.

Для системы с шлюзовой дисциплиной обслуживания заявок преимущество среднего времени пребывания при адаптивном опросе составляет 29,3% (27,8%, соотвественно, при исчерпывающем обслуживании очередей) по сравнению с обычным циклическим опросом, если в системе есть очереди с очень малой загрузкой. Для рассматриваемой системы упорядоченный адаптивный опрос дает преимущество в 2,8% по сравнению с адаптивным опросом (3,9% при исчерпывающем обслуживании очередей). А упорядоченный адаптивный опрос в свою очередь снижает среднее время пребывания в системе на

25,8% по сравнению с циклическим опросом (см. рис. 5) и на 22,9% при исчерпывающем обслуживании (см. рис. 6).

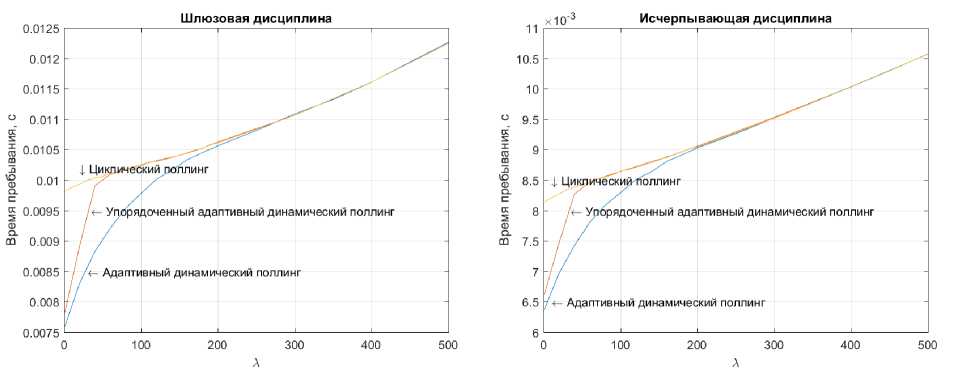
Рис. 5. Шлюзовая дисциплина.

Рис. 6. Исчерпывающая дисциплина.

3.    Заключение

В работе представлены некоторые результаты имитационного моделирования системы поллинга с циклическим порядком опроса, очередй и двумя адаптивными его разновидностями. Показано, что в некоторых случаях адаптивные механизмы опроса, очередей могут дать существенное снижение среднего времени пребывания заявки в системе в случае, если некоторые из очередей имеют относительно низкую загрузку, и не имеют смысла, в системах, все очереди которых имеют большую загрузку. Таким образом, адаптивные политики опроса могут быть более оптимальными с точки зрения средних времен пребывания в системе.