Исследование системы массового обслуживания со смещенными экспоненциальными входными распределениями

К системам с запаздыванием в науке и технике можно отнести системы автоматического регулирования, системы автоматического и дистанционного управления, телеметрии и др. В литературе по теории систем массового обслуживания (СМО) и ʙ Internet ресурсах нет упоминаний о таких системах со смещенными во времени входными распределениями.

В основе описания любой СМО, в том числе СМО с запаздыванием, лежит понятие рекуррентного потока [1], определяемого совокупностью функций распределения F 1 (t ) = F 2 ( t ) = ... = = F n ( t ) = ... = F ( t ) между поступающими требованиями. Далее мы рассмотрим случай, когда СМО образована двумя потоками, определяемыми функциями

1 - e ^{-y (} t ^- t 0 ) ,       t >  1 ₀;

0,       0 <  t <  t 0 ,

F ( t н

где y >  0, и потоки имеют одинаковое время запаздывания t ₀. B качестве математической модели таких систем предлагается рассматриваемая ниже СМО с запаздыванием.

Рассмотрим СМО, на вход которой поступают требования, случайные интервалы между кото- рыми распределены с функцией плотности (см. также рисунок 1) вида a (t) =

X e ^-X( t - t ⁰ ) ,

.       0,

t >  t 0 ;

0 <  t <  1 ₀.

Аналогично распределено и время обслужи- вания:

^-ц( t - t 0 )

b (t мц e     , t > t0;

0,      0 <  t <  t ₍

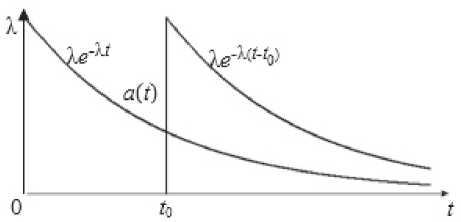
Рисунок 1. График функции плотности с запаздыванием (1)

Функции плотности (1) и (2) являются сдвинутыми вправо от нулевой точки на величину t0 экспоненциальными распределениями с двумя параметрами (X, 10) и (ц, 10), причем X< ц (см. рисунок 1). Таким образом, мы имеем СМО с запаздыванием во времени на величину 10 > 0. Заметим, что законы распределения (1) и (2) содержит два параметра, следовательно, они могут быть описаны двумя первыми моментами. Новую СМО, в отличие от классической, обозначим М -/М -/1.

Постановка и способ решения задачи

Методом спектрального разложения решения интегрального уравнения Линдли (ИУЛ) требу- ется получить результат по среднему времени ожидания в очереди, а также требуется оценить, как операция сдвига во времени скажется на характеристиках новой СМО М- / М- /1, и чем эта внешне схожая с классической СМО М/М/1 система будет от нее отличаться.

Для последующего применения метода спектрального разложения к решению данной зада- чи, сначала определим числовые характеристики интервала поступления требований и времени обслуживания. Для этого воспользуемся преобразованием Лапласа функций плотности (1)-(2):

A * ( s ) =

X e - t0 s s + X

^- t о s

B * ( s ) = H e— .             (4)

s + Ц

Первая производная функции (3) равна:

dA * (s) _ -X10e~t0s (s + X) - Xe-t0s ds "         (s + X)2         , а ее значение со знаком минус в точке s = 0: - dA * (s)

ds

s = 0

X ² 1 ₀ +X

X ²

= X + 1 0 -

По свойству преобразования Лапласа правая часть последнего выражения равна среднему значению интервалов между соседними требованиями входного потока

T x =X^{- 1} + 1 0 .                   (5)

Из равенства (5) следует, что интенсивность поступления требований X'= 1/ т_х в СМО М ^- /М ^- /1 определяется через параметры распределения (1) как

X' = X /(1 + X 1 ₀).                (6)

Поступая аналогично с функцией (4), находим среднее время обслуживания в системе

Т ц =ц^{- 1} + 1 о .                  (7)

Тогда интенсивность обслуживания требований ц' определяется через параметры распределения (2) из равенства (7):

ц' = ц /(1 + ц t ₀). (8)

Таким образом, интенсивности поступления X' и обслуживания ц' в системе М ^- /М ^- /1 напрямую зависят от интенсивностей X и ц классической системы и параметра сдвига t ₀.

Загрузка рассматриваемой системы, определя-eмая отношением интенсивностей поступления (6) и обслуживания (8), возросла в ^ + X t ⁰ раз по сравнению с системой М/М/1:

X' = X (1 + ц t ₀) ц' ц (1 + X t ₀)

Из равенств (5) и (7) следует, что в качестве входных параметров системы удобнее использовать средние значения интервалов т_х и т_ц , так как их отношение р = т_ц / т_х определяет загрузку СМО.

Определим начальный момент второго порядка интервалов поступления. Для этого находим значение второй производной от функции (3) при s = 0. Тогда

2 t 2

тО = to2 + — + ~т х 0 X Х2

и, с учетом того, что дисперсия интервалов для распределения (1) равна Dх =X-2, получим коэффициент вариации интервалов входного потока с x=(1 + X tо )-1.                 (10)

Аналогично определим коэффициент вариации времени обслуживания. Дисперсия этого времени Dц = ц-2, а коэффициент вариации c ц=(1 + ц 10 )-1.                 (11)

Заметим, что коэффициенты вариации c _х и с _ц меньшеединицыпри 1 ₀, X , ц> 0.

Полученные числовые характеристики позволяют сделать следующие предположения.

• 1.    Операция сдвига во времени приводит к

• 2.    В связи с тем, что коэффициенты вариации интервалов поступления с _х и времени обслуживания с _ц меньше единицы, мы имеем немарковскую модель массового обслуживания. Среднее время ожидания требования в очереди в такой си-cтеме должно быть меньше, чем в системе М/М/1

• 3.    Использование функций плотности (1) и (2) позволяет аппроксимировать исходные входные распределения, в отличие от классической СМО, на уровне двух первых моментов.

—         „       1 + ц t увеличению загрузки системы в 0 раз, чем

1 + X tо в классической системе М/М/1.

при одинаковом коэффициенте загрузки, так как c _X и c _y для системы М/М/1 равны единице.

Таким образом, мы выделили основные отличия рассматриваемой системы от классической СМО, но, как оказывается, между ними есть и много общего.

Определение среднего времени ожидания в очереди для системы M- / M- /1 на основе метода спектрального разложения ИУЛ

Основные характеристики системы G/G/1, как следует из [2], описываются известными из теории случайных процессов интегральными уравнениями типа Винера-Хопфа. Одно из этих уравнений в [2] выведено в форме интегрального уравнения Линдли։

y j W(у - и)dC(u), у > 0;

-to

0,           у < 0, где W (у) - функция распределения вероятностей времени ожидания требования в очереди, C (и) - аналогичная функция предельной случайной величины U = lim Un = xn - tn+1; xn - вре-n Hto мя обслуживания n-го требования Cn; tn+1 - ин-тeрвaл врeмeни мeжду поступлeниeм трeбовaний Cn и Cn+1.

Baжно зaмeтить, что интeгрaльнaя формa урaвнeния (12) имeeт мecто только для нeот-рицaтeльных знaчeний aргумeнтa y , тaк кaк для отрицaтeльных знaчeний aргумeнтa функция W ( у ) = 0.

Суть рeшeния ИУЛ (12) cпeктрaльным мeто-дом сводится к тому, чтобы для вырaжeния

A * ( - s ) B * ( s ) - 1             (13)

нaйти прeдстaвлeниe в видe произвeдeния двух множитeлeй, котороe дaвaло бы рaционaльную функцию от s [2]. Taким обрaзом, для нaхождe-ния рaспрeдeлeния врeмeни ожидaния нeобходи-мо слeдующee cпeктрaльноe рaзложeниe:

A * ( - s ) B * ( s ) - 1 = ^ ±M ,       (14)

V -^{( s} )

где ^+ (s) и V- (s) некоторые рациональные функции от s, которыe можно рaзложить нa мно- жители. Функции v+ (s) и у- (s) должны удов-лeтворять опрeдeлeнным условиям [2].

• 1.    Для Re ( s ) > 0 функция v₊ ( s ) является aнaлитичecкой бeз нулeй в этой полуплоскости.

• 2.    Для Re ( s ) < D функция v ( s ) является aнaлитичecкой бeз нулeй в этой полуплоскости, гдe D ‒ нeкоторaя положитeльнaя констaнтa,

опрeдeляeмaя из условия lim t Hto

a ( t ) ^D T <^to .

e

Кроме того, функции ^. ( s) и v ( s) должны облaдaть слeдующими свойствaми։

- для Re ( s ) > 0:   lim ^⁺ ( ) = 1;

^{v }}        I s 1^ s

- для

Re ( s ) < 0: lim ^ ( ^ = - 1.

^v ’        I S H”    s

Taким жe путeм получeны рeшeния для сис-тeм с гипeрэкспонeнциaльными входными рaс-прeдeлeниями в рaботax [3; 6-7].

Опрeдeлим тeпeрь cпeктрaльноe рaзложeниe (14) для рaспрeдeлeний (1)-(2) с учeтом прeоб-рaзовaний Лaплaca (3)-(4). Meтод cпeктрaльного рaзложeния для рeшeния ИУЛ (12) в этом случae дaeт

V + ( ^s ) = X e ^{0 s} y e ^- t ^{0 s} - 1

V _ ( s ) X- s y + s где v₊ ( s ) и v ( s ) должны быть рациональными функциями.

Выполнив нeсложныe вычислeния, получим

V₊ ( s ) Xy- ( X- s )( y + s ) s ( s + y-X )

V - ( s )     ( X- s )( y + s )     ( X- s )( y + s )

Taким обрaзом, покaзaтeли стeпeни у экспо-нeнт в числитeлe дроби обнуляются и тeм сaмым опeрaция сдвигa нивeлируeтся. Слeдовaтeльно, cпeктрaльныe рaзложeния рeшeния ИУЛ для систем М- /М- /1 и М/М/1 совпадают, так как функция

V₊ ( s ) s ( s + y-X )

V-( s) (X-s )(y + s)

являeтся спeктрaльным рaзложeниeм для рeшe-ния систeмы М/М/1 [1].

Совпaдeниe рaзложeния (17) с рeзультaтом для систeмы М/М/1 являeтся чисто внeшним, тaк как здесь параметры X и y не являются для системы М ^- /М ^- /1 интенсивностями поступления и обслуживaния соотвeтствeнно.

Далее следуя [2], в качестве функции v+ (s) выбирaeм v+( S ) =

S ( 5 + ц —X )

( ц + S )

которая не имеет нулей и полюсов в области Re ( s ) > 0, а в качестве функции ^Д s ) _Х — s , которая не имеет нулей в области Re ( s ) < X .

Постоянная K определяется из условия:

K = lim ^^ = lim ^{S + ц —X} = 1 - X/ц ,

S ,0 S s ,0 S + ц где параметры X и ц определяются выражениями (5) и (7) и отношение X / ц не определяет коэффициент загрузки как в случае системы М/М/1.

Преобразование Лапласа для функции распределения времени ожидания, согласно [2] имеет вид

Ф₊ ( S ) = -K- = ^{( 1} — ^{Х/Ц)(Ц + S} ) •

V + ( s )     ( s + ц-Х )

Следовательно, преобразование Лапласа функ- ции плотности времени ожидания

W * ( s ) = s Ф₊ ( s ) _

( 1 -Х/ц )( ц + s ) ( s + ц — X )

Найдем первую производную от (18): dW * ( s ) _ ds

( 1 — X/ц ) ( s + ц — X ) — ( 1 — Х/ц )( ц + s )

( s + ц — X )

—X ( 1 — X/ц )

( s + ц — X ) ²■

Τогда значение первой производной со знаком минус при ѕ = 0 будет равно

dW * ( s )	Х ( 1 — Х/ц )     X / ц
ds	s _ 0     ( ц —х ) 2     (ц —Х)

Отсюда среднее время ожидания

W _ ^{X ц} .               (19)

ц —X

Результат (19) полностью совпадает с результатом для системы М/М/1, где

W _^          (20)

1 — P при значении р_Х/ц. Таким образом, формулы для среднего времени ожидания для системы с запаздыванием М—/М— /1 и для системы М/М/1 совпадают при одинаковых значениях параметров X и ц, создавая при этом разные нагрузки на системы. Это интересный факт сходства двух различных систем.

Определение неизвестных параметров рассматриваемых распределений

Полученные числовые характеристики распределений (1) и (2) в виде равенств (5), (7), (10) и (11) позволяют определить неизвестные параметры X , ц и 1 ₀. Запишем их в виде системы уравнений

^{X +} t о ^{_ Т}х , (1 + X t оГ¹ _ c X , ц^{— 1 +} t 0 ^_Тц , (1 + ц t о ) ^{— 1} _ С ц ,

где числовые характеристики в правых частях системы будут входными параметрами системы для определения неизвестных параметров.

Система (21) является переопределенной, и поэтому мы получим ограничение на входные параметры СМО Тх, cх, тц и cц. Для решения системы из первого уравнения выразим t0: tо _ Тх — Х 1.

Второе уравнение дает 1/(1 + ХТ_Х — 1) _ c _х , откуда

Х_ 1/( c х Т х ).               (22)

Третье уравнение дает ц 1 + тх — X 1 _ тц, тогда ц_ ----г-           (23)

^Тц ^{— Т}х ( 1 ^— c х )

Из четвертого уравнения получим следующее ограничение:

1 , ^Х (1 — c х ) ^_ c ^ц , ^Тц ^—TX^{( 1 —} c X )

отсюда

^Тц ^{— T}X^{( 1 —} c X )

c ц ^_  ----------- ^{_ 1 —} ( 1 ^— c х )/Р ,

Тц где„, = Т- / Тх.

Окончательно коэффициент вариации времени обслуживания есть c ц_ 1 — р(1 — c х).               (24)

Τаким образом, входные параметры системы

М ^— /М ^— /1: Т_х , c _х , Т_ц и c _ц строго связаны соотношением (23).

Примеры расчета среднего времени ожидания для системы М"/М~/1

В качестве примера рассмотрим случаи разных нагрузок. Примем следующие значения входных параметров СМО: Тц _ 1, Тх _ 10 и cц _ 0,5. Тогда ограничение (24) при загрузке р _ 0,1 дает cX = 0,95. Далее определим неизвестные параметры X и ц.

Из (22) находим значение X = 1/9,5 = 2/19, а из (23) ц = 1/(1 - 10 • 0,5) = 2. Тогда среднее время ожидания из (19) есть W = 1/19/36/19 = 1/36. Для сравнения, среднее время ожидания для системы М/М/1 при такой же нагрузке р = 0,1 и интенсивности обслуживания ц = 1, равно

W _ ^р/^ц _0ЛЛ _ ¹

1 -р 0,9   9’ что в четыре раза больше, чем в системе с запаздыванием М- / М- /1.

В качестве второго примера рассмотрим случай высокой нагрузки: т_ц = 1, t_x = 10/9 и c _ц = 0,5. В этом случае получим загрузку р = 0,9; ограничение (24) дает c _X = 0,55, а равенства (22)(23) - значения X = 18/11 и ц = 2.

Тогда среднее время ожидания

W _ 18/11/2 _ 1811 _ 9

2 - 18/11 4 • 22 4

Система М/М/1 при той же нагрузке дает

W =

«•9/1 _ ₉

1 - 0,9

Расчетные данные хорошо согласуются с результатами двухмоментной аппроксимации [8].

Заключение

Рассмотренная СМО с запаздыванием М ^- / М ^- /1 позволяет рассчитать ее характеристики при коэффициентах вариации интервалов между поступлениями требований c _X и времени обслуживания c _ц , меньших единицы при некоторых ограничениях на входные параметры системы. Учитывая тот факт, что основные характеристики СМО, такие как средняя длина очереди, среднее количество требований в системе и др., являются производными от среднего времени ожидания, эти характеристики в работе не рассмотрены. Полученные результаты приводят к следующим выводам.

• 1.    Операция сдвига во времени приводит к

• 2.    В связи с тем, что коэффициенты вариации интервалов поступления c _X и времени обслуживания c _ц меньше единицы, мы получили немарковскую модель массового обслуживания G/G/1, для которой существует решение в замкнутой форме. Среднее время ожидания требования в

• 3.    Использование функций плотности (1)-(2) позволяет аппроксимировать исходные входные распределения в СМО на уровне двух первых моментов, в отличие от классической системы.

1 + ц tn увеличению загрузки системы в 0 раз по

1 + X 1 0 сравнению с классической системой М/М/1.

очереди в такой системе меньше, чем в системе М/М/1 при одинаковом коэффициенте загрузки.