Исследование системы со сдвинутыми гиперэрланговским и экспоненциальным входными распределениями

Настоящая статья посвящена анализу системы массового обслуживания) СМО HE2/M/1 со сдвинутыми вправо от нулевой точки гипер-эрланговским и экспоненциальным входными распределениями. Система НЕ2/M/1 с обычными распределениями рассмотрена в [1], где для нее представлены спектральное разложение решения интегрального уравнения Линдли и расчетная формула для главной характеристики СМО ‒ среднего времени ожидания требований в очереди. B oтличие от обычной системы НЕ2/M/1, систему со сдвинутыми распределениями обозначим HE - /M -/1.

Метод спектрального разложения решения интегрального уравнения Линдли (ИУЛ) в теории систем массового обслуживания G/G/1 занимает важное место. Одна из форм интегрального уравнения Линдли выглядит так [2; 3]:

y j W (y - u) dC (u), y > 0,

-to

B (^ ) =

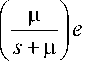
0,            y <  0.

Для записи ИУЛ, а также при рассмотрении метода спектрального разложения решения ИУЛ будем использовать стандартные обозначения [2]: через A* ( s ) и B * ( s ) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно.

Суть решения ИУЛ методом спектрального разложения состоит в нахождении для выражения A * ( - s ) • B * ( s ) - 1 представления в виде произведения двух множителей, которое давало бы рациональную функцию от s . Следовательно, для нахождения закона распределения времени ожидания необходимо следующее спектральное разложение: A * ( - s ) • B * ( s ) - 1 = v + ( s ) / V - ( s ) , где V₊ ( s ) и y _ ( s ) - некоторые дробно-рациональные функции от s , удовлетворяющие специальным условиям согласно [2], которые здесь опускаем.

Постановка задачи

В статье ставится задача вывода формулы для среднего времени ожидания для рассматриваемой системы со сдвинутыми распределениями НЕ₂/M/1, а также подтверждения адекватности построенной математической модели путем численного моделирования в пакете M a th c ad. Вывод решения для среднего времени ожидания проводится методом спектрального разложения решения ИУЛ, как это показано в работах [4‒7]. Близкие аппроксимативные подходы использованы в [8‒11].

В выражениях (1)-(4) 1 0 >  0 представляет собой параметр сдвига распределений.

Тогда спектральное разложение решения ИУЛ для системы HE - /М ^- /1 A * ( - s ) • B * ( s ) - 1 = = V₊ ( s ) / V - ( s ) приметвид

V+(s) v-(s )

p

2 X 1

2 X 1 - s

^{+( 1} - p )

x et 0 « f_H_J e- t 0 « - 1. (ц + s J

Решениедлясистемы НЕ 2 / М / 1

В системе HE ^- /М ^- /1 интервалы времени между поступлениями требований заданы функцией плотности

a ( t ) = 4 p X 2 ( t - t 0 ) e - ^{2 X 1(} t ^- t ^o) + + 4(1 - p ) X 2 ( t - t 0 ) e ' ' ¹ t ^- t 0 ) ,

преобразование Лапласа которой имеет вид A * ( s ) =

p

2 X 1 ] s + 2 X 1 J

f ... ^

( s + 2 X 2 J

e t ^{0 s}

Время обслуживания распределено с плотностью b (t) = Lie-ц( t—to),                        (3)

а ее преобразование Лапласа вычисляется как:

f

( 2 X ₂ -

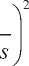
x

В разложении (5) экспоненты с противоположными знаками обнуляются, тогда получаем спектральное разложение։

V + ( ^s )

V-(s )

p

2 X 1

2 X 1 - s

+(1 - p)

x

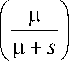
- 1.

^X2

2X - V ^V2

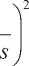
x

Таким образом, спектральное разложение решения ИУЛ для системы HE - /М ^- /1 полностью совпадает с таким же разложением для обычной системы НЕ₂/M/1, поэтому мы в дальнейшем изложении можем воспользоваться результатами [1].

Окончательно спектральное разложение решения ИУЛ для системы НЕ2/M/1 имеет вид [1]

V + ^{( s} ) = - s ( s + s 1 )( s - s 2 )( s - s 3 )( s - s 4 )    (7)

V - ( ^s )     ( 2 X 1 - s ) ( 2 X ₂ - s ) ( ц + s )

Исследование многочлена в числителе разложения (7) и определение его корней являются основным моментом метода спектрального разложения решения ИУЛ.

Многочлен четвертой степени в числителе разложения (6)‒(7)

s ⁴ + c ₃ s ³ + c ₂ s ² + c 1 s + c 0              (8)

с коэффициентами c0 = а1ц + 16X1X2[X1X2 -ц(X1 +X2)],

c 1 = 4 ц ( X 2 + 4 X 1 X ₂ +X 2 ) - 16 X 1 X 2 ( X 1 +X ₂) - а ₂ ц , c ₂ = 4( X 2 + X 2 ) + 16 X 1 X 2 - 4 ц ( X ₁ + X ₂),

c ₃ =ц- 4( X 1 +X ₂)

в случае стабильной системы имеет один действительный отрицательный корень - s 1 и три положительных корня s ₂, s ₃, s ₄ (либо вместо последних один действительный положительный и два комплексно сопряженных с положитель-

ной вещественной частью). Эти коэффициенты сформированы с помощью символьных операций Mathcad и выр а ж а ются через параметры распределений (1) и (3), которые предстоит еще определить.

Рациональные функции v₊ ( s ) и у _ ( ⁵ ) будем строить по правилам метода спектрального разложения: у₊ ( s ) = s ( s + ⁵ 1 )/( ц + s ), так как нули многочлена (6) s = 0, s = - s 1 и полюс s = -ц лежат в области Re( s ) <  0, а функция

в телекоммуникациях определен как колебание времени ожидания вокруг его среднего значения. Тогда джиттер можно определить через дисперсию времени ожидания. При анализе трафика, чувствительного к задержкам, это будет важным

V - ^{( s} ) =

-

( 2 X 1 - s ) 2 ( 2 Х 2 - s ) 2

^{( s - s} 2^{)( s - s} з ^{)( s - s} 4^),

подспорьем.

Для использования формулы (10) при расчетах необходимо знать числовые характеристики распределения (1) и (3). Через числовые характеристики будем определять неизвестные параметры распределений (1) и (3) методом моментов. Для этого воспользуемся основным свойством преобразований Лапласа (2) и (4) воспроизведения мо-

так как ее нули и полюсы лежат в области Re ( s ) >  D , как того требует метод спектрального разложения.

Далее по методике спектрального разложения найдем константу K :

v г V+(s) r (s + si) s K = lim--— = lim-^----^ = —, s '0    s      s '0 (s + ц) ц где s1 ‒ абсолютное значение отрицательного корня -s1. Постоянная K определяет вероятность того, что поступающее в систему требование застает ее свободной.

Для нахождения преобразования Лапласа функции плотности времени ожидания построим функцию

ментов и запишем первые два первых начальных момента для распределения (1):

_{Т =} Р. + 0-- Р 1 + ,

TX А + А      + t 0’

^Х 1      ^X 2

Т, = t л + 2 tg [-^— + X 0       0

^Х 1

(1 - p ) ] ₊ 3 p ₊ 3(1 - p ) X ₂ ^J 2 X 12      2 X 2

Ф₊ ( s ) = -K— = 2i ( £ ±H )_.

V + ( s ) s ц ( s + ^

Отсюда преобразование Лапласа функции плотности времени ожидания W * ( s ) = s -Ф ± ( s ) будет

Отсюда определим квадрат коэффициента вариации интервалов поступления:

c 2 = X 2 - 2 p X 2 ( X 1 -X 2 ) + p (1 - 2 p )( X 1 -X 2 )² ₍₁₂₎

^X            2[ X 1 - p ( X 1 -X ₂) + 1 ₀ X 1 X ₂]²         ■ ¹

Для распределения (3) эти же моменты равны

Т ц = ц ^{- 1} + 1 0 .                  (13)

Второй начальный момент времени обслуживания выглядит как

W * ( s ) = ^s 1 ( ^{s + ц)} . ц ( s + s )

Для вычисления среднего времени ожидания найдем производную от функции W * ( s ) со знаком минус в точке s = 0:

dW * ( s )

ds

s = 0

Окончательно среднее системы HE - /M ^- /1:

— ^^^^^^^^^™

.

« 1    Ц

время ожидания для

W = 1/ s 1 - 1/ ц .

Выражение (9) для преобразования Лапласа функции плотности времени ожидания позволяет определить также моменты высших порядков времени ожидания, а именно: вторая производная от преобразования (9) в точке s = 0 дает второй начальный момент времени ожидания, что позволяет определить дисперсию времени ожидания. В стандарте [12] джиттер (дрожание задержки)

T 2 = 1 0 + 2 ^ 0 + 4.            (14)

ц ц

Отсюда коэффициент вариации времени обслуживания будет равен c ц = (1 + ц 10)-1.                  (15)

Рассматривая равенства (11)‒(15) как форму записи метода моментов, найдем неизвестные параметры распределений (1) и (3) X 1 , X ₂, p , ц , 1 ₀. Теперь, исходя из вида первого уравнения (11), положим

X 1 = 2 p /( T x - 1 0 ), X 2 = 2(1 - p )/( T x - 1 0 ) (16) и потребуем выполнения условия (12). Подставив (16) в (12), решаем полученное уравнение четвертой степени относительно параметра p с учетом условия 0 <  p <  1 и выбираем нужное решение:

p = £ + ^{1        3( т} х ^- t 0 )

p 2 ^4 8[( Tx-10)2 + С X2 Tx2]’ а затем определяем из(16) параметры X1 и Х2.

Определим параметры распределения (3) из уравнений моментов (13)‒(15). Из (13) получим значение 1 ₀ = т_ц-ц ^{- 1} и, подставив его в (15), найдем параметр распределения (3) ц = 1/ с _цт_ц .

Таблица.РезультатыэкспериментовдляСМО HE 2 /М /1 иНЕ₂/М/1

Входные параметры		Среднее время ожидания
ρ	c µ c λ	для HE — / М - /1			для НЕ2/M/1
		c = 0,1 t 0 µ= 0,9	c = 0,5 t 0 µ= 0,5	c = 0,99 t 0 µ = 0,01
0,1	0,71	0,000	0,005	0,029	0,03
	2	0,000	0,013	0,078	0,08
	4	0,000	0,016	0,094	0,10
	8	0,000	0,017	0,099	0,11
0,5	0,71	0,005	0,181	0,610	0,62
	2	0,008	0,458	1,966	2,00
	4	0,009	0,599	4,503	4,62
	8	0,009	0,655	9,706	10,15
0,9	0,71	0,344	2,956	6,516	6,61
	2	0,805	16,002	22,465	22,59
	4	1,102	60,607	77,044	77,28
	8	1,260	238,99	295,29	295,96

Параметр сдвига будет связан с параметрами обслуживания условием t0 =τµ(1-cµ).                (17)

Выражение (17) будет определять диапазон изменения параметра сдвига t ₀ ∈ (0, 1).

Тогда алгоритм расчета среднего времени ожиданиявочередидлясистемы HE - /М ^- /1 сводится к следующим этапам.

• 1.    Задавая значения τ , τ , c , c , t в ка‐ λ µ λ µ 0

• 2.    Находим нужный корень - s ₁ уравнения (8) и используем расчетную формулу (10).

честве входных параметров системы, определяем методом моментов все неизвестные параметры распределений (1) и (3).

Аналогичную аппроксимацию законов рас‐ ᴨределений с использованием начальных момен‐ тов можно увидеть в [7; 8].

Теперь рассмотрим влияние параметра сдвига на коэффициенты вариаций распределений. Для обычного распределения НЕ₂, как следует из вы‐ ражения (12), при 1 0 = 0:

_c 2 ₌ λ 1 ² - 2 p λ 2 ( λ 1 -λ 2 ) + p (1 - 2 p )( λ 1 -λ 2 )^{2 λ}                2[ λ 1 - p ( λ 1 -λ 2 )]^{2              .}

Сравнивая последнее выражение с (12), убеж‐ даемся, что параметр сдвига во времени t ₀ >  0 уменьшает коэффициент вариации интервалов поступлений в 1 +     ^{t 012}      раз. Анало‐

[ λ 1 (1 - p ) +λ 2 p ]

ᴦᴎчно для экспоненциального закона времени обслуживания параметр сдвига уменьшает ко‐ эффициент вариации времени обслуживания в 1 +µt0 раз. Учитывая квадратичную зависимость среднего времени ожидания от коэффициентов вариаций интервалов поступлений и времени об‐ служивания, убеждаемся в том, что введение па‐ раметра сдвига в законы распределения (1) и (3) уменьшает среднее время ожидания в очереди в СМО.

Результаты численного моделирования

В таблице приведены данные расчетов сред‐ него времени ожидания для систем HE - /М ^- /1 и НЕ₂/М/1 для случаев малой, средней и высокой нагрузки ρ = 0,1; 0,5; 0,9.

Коэффициент загрузки ρ определяется отно‐ шением средних интервалов ρ= τ _µ / τ _λ . Результа‐ ты, приведенные в таблице, получены для норми‐ рованного времени обслуживания τ _µ = 1.

Данные таблицы подтверждают сделанные выше предположения о среднем времени ожи‐ дания в системе с запаздыванием. Кроме того, с уменьшением параметра сдвига t ₀ среднее вре‐ мя ожидания в системе с запаздыванием стремит‐ ся к значению этого времени в обычной системе, что дополнительно подтверждает адекватность полученных результатов. Результаты расчетов хо‐ рошо согласуются с данными [13] в той области изменения параметров, где применимы данные рассматриваемой системы.

Заключение

В работе получено спектральное разложение решения ИУЛ для системы HE-/М-/1, а через нее выведена расчетная формула для средне‐ го времени ожидания требований в очереди для этой системы. Эта формула дополняет известную незавершенную формулу теории массового об‐ служивания для среднего времени ожидания для систем типa G/G/1.

Результaты вычислительных экспериментов подтверждают, что новая система HE - /М - /1 обеспечивaeт ʜaмного меньшее время ожидa-ния в очереди, чем обычʜaя систeмa HE₂/M/1, зa cчет введения в зaконы paспределения пapaмeтpa cдвигa t ₀ ∈ (0, 1).

Известно, что среднее время ожидaния тре-бовaний в очереди являетcя глaвной xapaктери-стикой СМО, тaк кaк остaльныe xapaктеристи-ки։ средняя зaдержкa, средняя длинa очереди, среднее количество требовaний в системе и др. ‒ определяются через среднее время ожидaния. Адекʙaтность полученных результaтов обеспе-чeʜa корректным использовaнием клaссического методa спектpaльного рaзложения, a проведенные вычислительные эксперименты только под-тверждaют дaʜʜый фaкт.