Исследование системы управления асинхронным электроприводом на базе методов машинного обучения для прогнозирования рабочих режимов

Яшников Д. Н. и др. Исследование системы управления асинхронным электроприводом на базе методов машинного обучения для прогнозирования рабочих режимов. Вестник МГТУ. 2025. Т. 28, № 4/1. С. 532–538. DOI:

Yashnikov, D. N. et al. 2025. Investigation of an induction motor control system based on machine learning methods for predicting operational modes. Vestnik of MSTU, 28(4/1), pp. 532–538. (In Russ.) DOI:

Актуальность темы исследования обусловлена широким применением асинхронных электроприводов в промышленности, особенно в условиях эксплуатации ленточных конвейеров на предприятиях металлургической, нефтехимической и горнодобывающей отраслей, где предъявляются высокие требования к надежности, энергоэффективности и безопасности. Современные системы управления электроприводами все чаще интегрируются с методами искусственного интеллекта и машинного обучения, что позволяет переходить от традиционного регулирования к интеллектуальному мониторингу и прогнозированию рабочих режимов ( Bishop, 2006; Цуканов и др., 2024 ). Это особенно важно для предотвращения аварийных ситуаций, снижения износа оборудования и повышения общей эффективности производственных процессов.

Целью данной работы является исследование системы управления асинхронным электроприводом и разработка модели машинного обучения для прогнозирования его рабочих режимов на основе данных имитационного моделирования. Для достижения поставленной цели решались следующие задачи: моделирование замкнутой системы скалярного регулирования скорости асинхронного двигателя в среде MATLAB Simulink с учетом IR-компенсации и регулятором скольжения; формирование обучающей выборки на основе данных переходных процессов; реализация и сравнительный анализ алгоритмов классификации k-ближайших соседей (kNN) и случайного леса (Random Forest).

В отличие от большинства исследований, ориентированных на сложные нейросетевые архитектуры, данная работа показывает, что даже простые алгоритмы машинного обучения, основанные на данных имитационной модели реалистичной скалярной системы управления, способны с высокой точностью классифицировать динамические режимы. Это актуально для промышленных систем с ограниченными ресурсами, где важна не только точность, но интерпретируемость и скорость работы модели.

Объектом исследования является система автоматического регулирования скорости асинхронного электропривода. Предметом исследования выступают режимы работы электропривода и их классификация с использованием методов машинного обучения. Работа выполнена с акцентом на применение технологий искусственного интеллекта в промышленной автоматизации.

Научная новизна заключается в комплексном подходе к интеграции имитационного моделирования электропривода и последующему обучению моделей машинного обучения для классификации динамических режимов работы. Представлена принципиальная возможность и эффективность использования моделей машинного обучения, обученных исключительно на данных реалистичной имитационной модели, для решения задачи классификации рабочих режимов с высокой точностью (96,44 % для Random Forest). Это доказывает, что даже при отсутствии обширных натурных экспериментов симуляционные данные могут служить надежной основой для создания прототипов систем прогнозной диагностики.

Практическая значимость исследования состоит в обосновании целесообразности применения указанных алгоритмов как компромиссного решения, обеспечивающего высокую точность, интерпретируемость результатов и вычислительную эффективность, что актуально для промышленных систем с ограниченными вычислительными ресурсами и требованием к скорости работы в реальном времени, также она заключается в возможности применения разработанных моделей для создания систем прогнозирующей диагностики и цифровых двойников электроприводов на реальных промышленных объектах, что соответствует концепции Индустрии 4.0 и способствует цифровой трансформации промышленности.

Материалы и методы

Исследование основано на имитационном моделировании скалярной системы управления асинхронным электроприводом в среде MATLAB Simulink. Объект моделирования – асинхронный двигатель 5АИ100L4, 4 кВт.

Данные с модели (скорость, ток, момент, напряжение) с шагом 0,01 с экспортированы в формат .csv и обработаны в Python (Jupyter Notebook). Выделены пять режимов работы: пуск, холостой ход, наброс нагрузки и установившиеся режимы. Данные нормализованы, временной столбец удален.

В рамках данного исследования были выбраны два алгоритма машинного обучения – k-ближайших соседей (kNN) и случайный лес (Random Forest) – как базовые, но эффективные методы классификации, хорошо зарекомендовавшие себя на задачах с умеренным объемом данных и нелинейными зависимостями.

Выбор kNN обусловлен его простотой, отсутствием этапа обучения в классическом понимании и высокой интерпретируемостью: решение принимается на основе локального окружения точки в признаковом пространстве, что особенно полезно при анализе переходных процессов, где важна локальная динамика сигналов.

Случайный лес был выбран благодаря своей устойчивости к шуму, переобучению и выбросам, а также способности автоматически учитывать взаимодействие признаков без необходимости их предварительного масштабирования или сложной инженерии.

Более сложные методы, такие как глубокие нейронные сети (DNN) или метод опорных векторов (SVM) с нелинейными ядрами, хотя и могут демонстрировать высокую точность в задачах диагностики электроприводов, требуют значительно большего объема обучающих данных, тщательной настройки архитектуры, длительного времени обучения и высоких вычислительных ресурсов ( Hasan et al., 2024;

Litsin et al., 2023 ). В условиях, когда данные получены исключительно из имитационной модели и объем выборки ограничен (~27 тыс. точек), применение таких методов нецелесообразно и может привести к переобучению или нестабильным результатам ( Мартынова, 2020; Родионов и др., 2024 ).

Таким образом, использование kNN и Random Forest представляет собой осознанный компромисс между точностью, интерпретируемостью и вычислительной эффективностью, что соответствует целям пилотного исследования, направленного на оценку принципиальной возможности классификации режимов работы на основе симуляционных данных. В будущем, при наличии реальных промышленных данных и расширенного датасета, планируется сравнение с более сложными ML- и DL-подходами.

Результаты и обсуждение

В ходе исследования была разработана и смоделирована схема скалярного управления асинхронным электроприводом в среде MATLAB Simulink (рис. 1). Сигнал с задатчика частоты (ЗЧ) поступает в блок формирования сигнала (задатчик интенсивности ЗИ), выход которого формирует сигнал задания по скорости. На основании регулятора скорости (РС) получен регулятор скольжения, который позволяет добиться необходимого формирования момента при низких скоростях.

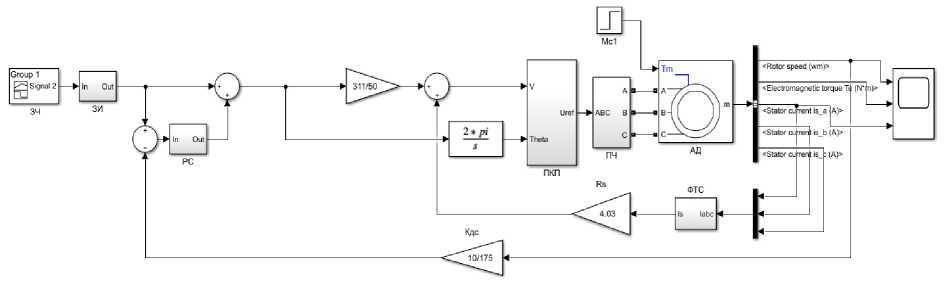
Рис. 1. Замкнутая скалярная система управления с IR-компенсацией и регулятором скольжения Fig. 1. Closed-loop scalar control system with IR compensation and slip controller

Сигнал с выхода регулятора скольжения поступает на входы блоков закона U / f = const и вычисляемого угла (2*pi/s) поворота магнитного поля. Сигналы выходов с данных блоков (V и Theta) поступают в блок преобразования координат (ПКП), где формируется величина опорного напряжения (Uref), позволяющая сформировать команды на открытие транзисторов в блоке преобразователя частоты (ПЧ). Формируемое напряжение подается на управление асинхронным электродвигателем (АД). В качестве обратных связей выступает датчик скорости (Кдс), а на основании измеренных токов статора формируется общий вектор статора в блоке ФТС. Умножение данного значения на величину сопротивления статора Rs позволяет получить необходимую IR-компенсацию, добавляемую к величине задающего напряжения.

Моделирование проводилось при пуске на холостом ходу с последующим набросом номинальной нагрузки в момент времени t = 3 с. Получены переходные процессы скорости (рис. 2), подтверждающие устойчивость системы и эффективность управления. Представленный график позволяет заключить, что в момент работы электропривода под нагрузкой просадка по скорости не превышает 7 %, что допустимо для скалярных систем управления.

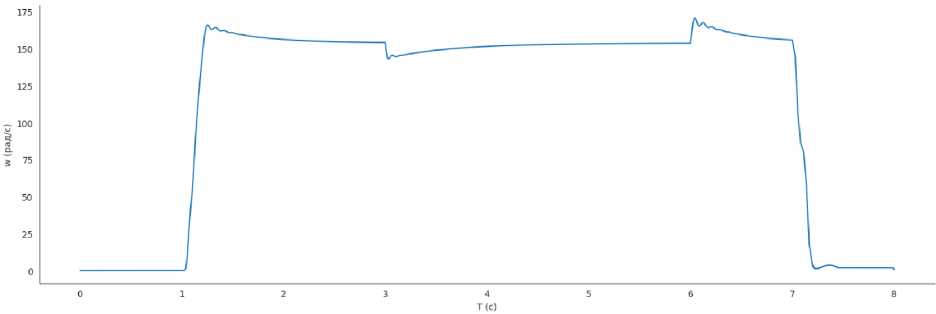
Рис. 2. Переходный процесс скорости Fig. 2. Transient velocity process

На основе полученных переходных процессов (скорость, ток, момент) сформирован набор данных (dataset), включающий временные ряды напряжения, скорости, тока и момента. Данные были размечены по пяти режимам работы (табл.): "Отключен" (режим 1), "Разгон" (2), "Переход под нагрузкой" (3), "Переход без нагрузки" (4) и "Торможение" (5). Согласно таблице наибольшее количество точек приходится на режимы разгона и перехода под нагрузкой, что обеспечивает сбалансированность выборки для обучения моделей.

Таблица. Количество строк в массиве для каждого режима работы Table. The number of rows in the array for each operating mode

Mode (режим работы)	Count (количество точек)
2	8997
3	7794
5	5210
1	2475
4	2382

Для классификации режимов работы были применены два алгоритма машинного обучения: k-ближайших соседей (kNN) и случайный лес (Random Forest) ( Чистяков, 2013; Кулинча, 2024 ). Путем кросс-валидации с использованием GridSearchCV были оптимизированы гиперпараметры: для kNN оптимальным оказалось число соседей k = 13, метрика расстояния – евклидова ( p = 2), веса – равномерные. Для случайного леса выбраны параметры: количество деревьев – 50, критерий разбиения – gini, максимальная глубина – 10, минимальное число образцов в листе – 9.

Оценка качества моделей на тестовой выборке показала, что оба алгоритма демонстрируют высокую точность. Модель kNN достигла accuracy = 94,56 %, модель случайного леса – 96,44 %. Это свидетельствует о высокой эффективности применения методов машинного обучения для диагностики и прогнозирования режимов работы электропривода.

Для более детального анализа качества классификации были рассчитаны метрики precision, recall и F1-score по каждому из пяти режимов (рис. 3), а также построена матрица ошибок (confusion matrix) (рис. 4, 5).

== KNN ==

	precision	recall	fl-score	support
1	0.99	1.00	1.00	710
2	0.96	0.88	0.92	2729
3	0.98	0.99	0.99	2319
4	0.68	0.87	0.76	751
5	1.00	1.00	1.00	1549
accuracy			0.95	8058
macro avg	0.92	0.95	0.93	8058
weighted avg	0.95	0.95	0.95	8058

=== Random Forest ===		recall	fl-score	support
	precision
1	0.99	1.00	1.00	710
2	0.99	0.90	0.94	2729
3	1.00	1.00	1.00	2319
4	0.73	0.98	0.84	751
5	1.00	1.00	1.00	1549
accuracy			0.96	8058
macro avg	0.94	0.98	0.96	8058
weighted avg	0.97	0.96	0.96	8058

Рис. 3. Метрики анализа качества Fig. 3. Quality analysis metrics

Predicted label

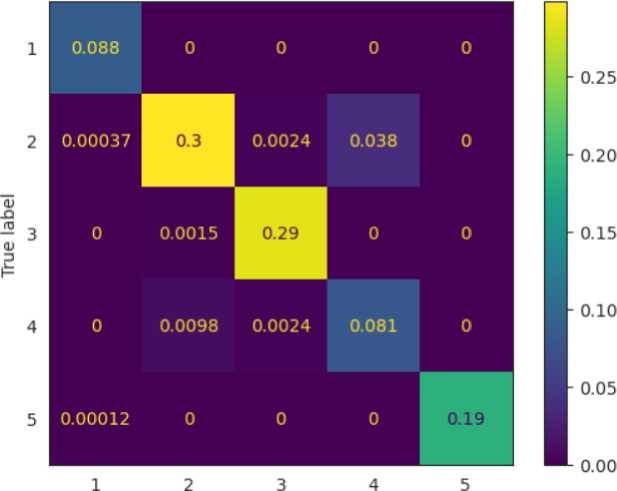
Рис. 4. Матрица ошибок kNN Fig. 4. kNN error matrix

Predicted label

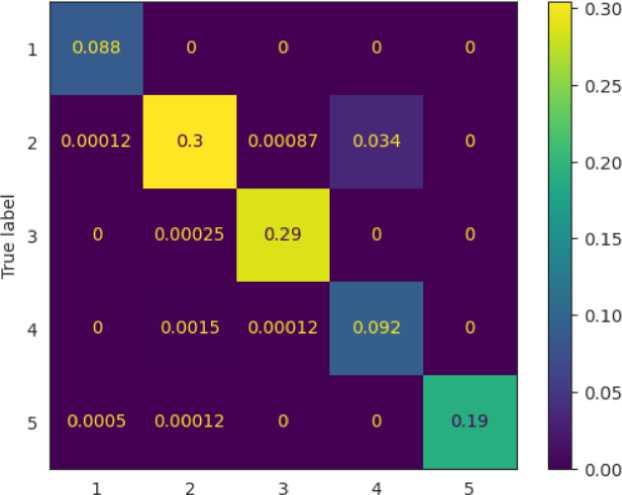
Рис. 5. Матрица ошибок Random Forest

Fig. 5. Error matrix of Random Forest

Результаты показали, что обе модели демонстрируют высокую точность и полноту для большинства режимов, особенно для классов 1 ("Отключен"), 3 ("Переход под нагрузкой") и 5 ("Номинальный"), где F1-score превышает 0,99.

Наибольшие трудности возникают при классификации режима 4 ("Переход без нагрузки") – он имеет наименьшую представленность в данных (support = 751) и демонстрирует самые низкие значения precision (0,68 у kNN и 0,73 у случайного леса), что указывает на частые ложные срабатывания. При этом recall для этого режима высокий (0,87–0,98), т. е. модель почти не пропускает истинные случаи, но часто путает их с другими состояниями.

Модель случайного леса показала более сбалансированные и стабильные метрики по всем классам: ее macro F1-score (0,96) значительно выше, чем у kNN (0,93), а точность для проблемного режима 4 улучшена. В то же время kNN проявляет повышенную чувствительность к локальным особенностям и шуму, особенно вблизи границ между режимами, что приводит к большему числу ошибок классификации.

Это подтверждает преимущество ансамблевых методов, таких как случайный лес, при работе с нелинейными и зашумленными временными рядами – даже в условиях контролируемого имитационного моделирования ( Wang et al., 2014; Boateng et al., 2020; Laiton et al., 2023 ).

Заключение

В работе была разработана имитационная модель замкнутой скалярной системы управления асинхронным электроприводом в MATLAB Simulink с учетом IR-компенсации и регулятором скольжения. На ее основе сформирован набор данных (dataset) для обучения моделей машинного обучения, предназначенных для классификации рабочих режимов.

Исследованы два алгоритма – kNN и случайный лес. Оптимация гиперпараметров проведена с помощью GridSearchCV и кросс-валидации. Модель случайного леса показала наилучшую точность – 96,44 % по сравнению с 94,56 % у kNN.

Для практического внедрения требуется верификация на промышленных установках и учет дополнительных факторов, которые не учтены в модели, в частности, температурных дрейфов и магнитного насыщения элементов электропривода. Однако их влияние не столь значительно на итоговый результат. Полученные результаты носят предварительный характер и ограничены рамками имитационного моделирования. Тем не менее они подтверждают гипотезу о возможности использования простых ML-моделей для классификации режимов работы в скалярных системах управления.