Метод гидравлического разрыва пласта является эффективным методом увеличения дебита скважин в низкопроницаемых коллекторах.

Кроме того, за счет созданных длинных трещин разрыва в зоне дренирования скважин изменяется направление фильтрационных потоков, инициируя увеличение дебитов окружающих скважин.

Механика породы при ГРП предполагает, что при глубинах больше 1000м в пласте образуется только вертикальная трещина, которая всегда имеет два кры- ла, симметричных геометрически, закреплена внутренне и не меняет свои размеры: длину и ширину [1,2].

Существует две основные модели, одна из которых предполагает «высокую проводимость», где падение давления внутри трещины незначительное и другая модель – «низкая проводимость», в которой считается, что давление вдоль трещины падает значительно.

Для обоснования режимов фильтрационных потоков из пласта в скважину, а также дебита и продуктивности после ГРП применяют следующие безразмерные параметры:

2 π⋅ ^kh ⋅∆ P

1. Безразмерная депрессия Pd =        µ     ; (1)

Q ⋅ b

2. Относительный дебит

η⋅ b ; (2)

0.532 ⋅ ^{kh µ}

• 3.    Безразмерное время t = χ ⋅ t ; (3) L TP

• 4.    Безразмерная к • W

  проводимость

  
  

  трещины

  
  
5. Параметр Пратса a

F = ^{kТ ⋅ W}; (4)

CД   k⋅L

π⋅k⋅L

TP

PR =2⋅k ⋅W

^π ; (5)

2 ⋅ FCД

• 6.    Коэффициент проникновения трещины

  
  
  

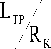
где kh – гидропроводность пласта, мкм2⋅см/(мПа⋅с); µ kT⋅W – проводимость трещины, мкм2⋅м;

η – коэффициент продуктивности скважины м3/(сут⋅МПа);

Q – дебит скважины, м3/сут;

Δ Р – депрессия, МПа;

• b – объемный коэффициент, б/р;

• χ – пьезопроводность пласта, м²/с;

• t – время, с;

• L_TP – полудлина трещины, м;

  k_T – проницаемость трещины, мкм²;

  k – проницаемость пласта, мкм²;

  R К – радиус дренирования, м.

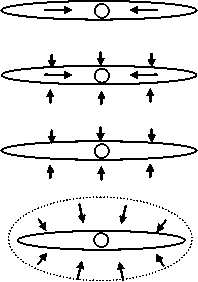
  В пластах, подвергнутых гидроразрыву, во время восстановления (или падения) давления могут наблюдаться четыре периода существования фильтрационного потока, отделенные друг от друга переходными периодами (рис. 1, 2):

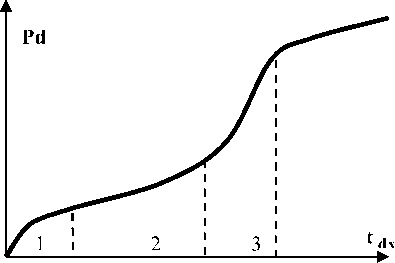
  • 1.    Линейный поток в трещине. Длительность такого периода может быть ничтожно мала и замаскирована влиянием притока в стволе скважины. В течение этого периода большая часть жидкости, поступающей в ствол скважины, образуется за счет расширения жидкости в трещине.

  • 2.    Билинейный поток, когда жидкость перетекает из пласта в трещину линейно, а эффекты в кончике трещины не влияют на поведение скважины.

  • 3.    Линейный поток из пласта имеет место только при высокой проводимости трещины.

  • 4.    Псевдорадиальный поток возникает при любых проводимостях трещины, чем выше проводимость, тем позднее возникает структура дренирования, которую можно считать в основном радиальной.

  
  

  При интерпретации КВД скважины после ГРП используются четыре основных метода:

  • 1.    Методы, основанные на анализе линейного или билинейного режима потока, если они имеют место;

  • 2.    Метод, предполагающий, что псевдорадиаль-

  
  

  ный режим потока достигнут;

  3. Использование типовых кривых или залежи путем анализа и сопоставления.

  Предположение о линейном притоке из совершенно справедливо при добыче

  
  

  высокопроводимую трещину с

  
  

  L TP вплоть до момента времени

  
  

  окончания периода притока скважины.

  
  

  модели

  
  

  пласта через

  
  

  полудлиной трещины

  t <       ^TP после

  X

  жидкости  в  ствол

  
  

  На логарифмическом графике lg A P - lgt линейный поток характеризуется прямой с наклоном ½.

  Процедура анализа КВД при линейном режиме такова:

  1. построить график КВД в координатах A P -

  
  
  
  
  

  Линейный поток в трещине

  Билинейный поток

  Линейный поток

  Псевдорадиальный поток

  
  

  T + 1

  t

  
  

  ;

  
  

  определить наклон i 2 линейного участка;

  по величине проницаемости k, упругоемкости

  
  

  Р * пласта определить полудлину трещины -_тр с

  
  

  _ A, - Q - Ь н ПТ TP      L - h          *

  помощью уравнения:         ²      «k ^e ; (6)

  На логарифмическом графике  lg A P

  
  

  _–

  
  

  lgt

  
  

  билинейный поток характеризуется прямой с наклоном ¼.

  Для определения параметров трещины строят график в координатах

  
  

  A P

  
  

  T + 1

  
  

  _–

  
  

  t

  
  

  и по уклону прямолинейного

  
  

  участка i₃ вычисляют проводимость трещины Кт - W по формуле:

  
  

  к_т - w = А₂ -

  
  

  Q^

  I ^{h -} i 3 J

  
  
  
  

  V^k-ц-Р

  
  

  ; (7)

  *

  
  

  Рис. 1. Схема фильтрационных потоков вокруг трещины ГРП во время восстановления или падения давления в пласте.

  
  
  

  где А 1 и А 2 , коэффициенты, зависящие от размерности времени t (сек, мин, час).

  
  

  Рис. 2. График типовой кривой восстановления (падения) давления скважины с ГРП в безразмерных координатах.

  
  

  При интерпретации КВД мы считаем, что поток псевдорадиальный, когда завершается трансформация площади дренирования от прямоугольной через эллиптическую (переходный поток) к почти радиальной. Тогда уравнения, выведенные для строго радиального потока, можно применять с малой погрешностью.

  Время, необходимое для достижения псевдоради-ального потока равно:

  t « 1 + 3 -TP при F_Cfl = 0,031 + 31

  Когда псевдорадиальный режим достигнут, для расчета гидропроводности kh/ ц , проницаемости k,

  
  

скин-фактора  St  пласта можно воспользоваться графиком КВД в полулогарифмических координатах

A P - _lg T±l t