Исследование сложной динамической системы ротор-опора-корпус газотурбинного двигателя с помощью многомассовых реологических моделей

Самарский государственный аэрокосмический университет

В работе приведены исследования динамики системы ротор ‒ опора - статор газотурбинного двигателя с помощью многомассовых реологических моделей. Получены амплитудно-частотные характеристики ротора, демпфера и корпуса, а также зависимости виброскорости и виброускорения в этих элементах двигателя.

Современные турбомашины, как правило, работают на рабочих оборотах, превышающих первую, а порой и вторую критические скорости. Динамическое состояние роторной машины, характеризуемое спектром собственных частот, уровнем вибрации статора, амплитудой колебаний ротора, а также усилиями и динамическими напряжениями, действующими на элементы машины, определяется жесткостью и демпфированием в опорах. Поэтому необходима оптимизация этих параметров с целью обеспечения тактико-технических требований, предъявляемых к изделию. Основная причина вибрации в газотурбинных двигателях (ГТД) ‒ несбалансированность масс ротора. Вращающийся ротор 1 (рис.1) генерирует центробежную возбуждающую силу, которую можно представить в виде F_в= ∆ω ²sin ω t , где t - время, ∆ -дисбаланс, а ω - частота вращения ротора. Возбуждающая гармоническая нагрузка F_в через подшипники 2, 3 и 4 опор ротора, трансформируясь до величины F_к , передается на корпус 5 опоры, что вызывает вибрацию статора 6. Уровень вибрации статора, замеряемый на корпусе с помощью датчиков виброскорости 7, зависит от возбуждающих нагрузок, обусловленных величиной и распределением дисбаланса ротора.

Динамическая балансировка ротора на собственных опорах улучшает вибрационное состояние двигателя, но не снимает полностью проблему повышенной вибрации, так как в процессе работы возникают дисбалансы: температурный, вызываемый тепловыми де- формациями ротора, и аэродинамический, обусловленный технологическим разбросом геометрических параметров лопаток.

В опорах роторов, у которых рабочие обороты близки или превышают собственную частоту, для ограничения амплитуды колебаний на околорезонансных и резонансных режимах при использовании подшипников качения необходимо дополнительное демпфирование. В настоящее время для снижения уровня вибрации широкое применение в ГТД нашли упругодемпферные опоры роторов с гидродинамическими демпферами (ГДД) [1, 2].

На подшипник качения 2 передней опо-

Рис.1. Схема свободной турбины изделия НК-12 СТ:

1 - ротор с диском турбины;

2 - роликовый подшипник передней опоры;

3 - роликовый подшипник задней опоры;

4 - шариковый подшипник задней опоры;

5 - корпус опоры; 6 - корпус статора;

7 - датчик замера вибрации на корпусе статора ры изделия НК-12СТ (рис.1) смонтирована (рис.2) втулка-вибратор 1, установленная во втулку статора 3 с зазором 5 величиной 8 = 0,13... 0,15 мм. Зазор заполняется маслом, поступающим затем через систему питающих каналов на смазку подшипника. От вращения втулка-вибратор 1 фиксируется штифтом 4, однако ей оставлена свобода прецессионного движения, т.е. зазор, заполненный жидкостью, выполняет роль ГДД. В этом случае динамическое поведение системы характеризуется еще одним параметром - амплитудой колебания в демпфере втулки-вибратора. При колебаниях втулки-вибратора 1 смазка выдавливаться из демпферного зазора и за счет сил вязкого трения происходит демпфирование колебаний ротора. Величина демпфирования и, следовательно, уровень вибрации на корпусе зависят от амплитуды колебаний в демпфере относительно корпуса (которую можно записать в виде хк - хд) и степени герметизации демпферного зазора. Герметизация демпферного зазора в рассматриваемой конструкции ГДД осуществляется с помощью упругих колец 6, которые с целью оптимизации упругих и уплотнительных свойств изготавливались из различных материалов: резины, материала МР и многожильного троса. Для оценки виброзащитных свойств упругодемпферной опоры, определяющих уровень вибрации корпуса, обычно используют коэффициент передачи амплитуды силы через опору на корпус ц с=Fk /Fe, где Fk - усилие, передаваемое на корпус [3]. Однако такой подход не позволяет идентифицировать результаты теоретического расчета с экспериментом на натурных изделиях, так как на корпусе двигателя в процессе эксплуатации замеряется уровень виброскорости [4], который зависит не только от виброзащитных свойств опоры, дисбаланса и массы ротора, но также от массы статорной части и жесткости ее подвески. В связи с этим при теоретическом исследовании динамики ГТД необходимо рассматривать как минимум двухмассовую модель системы ротор - корпус (рис.За), где тр- масса ротора, приходящаяся на опору, а mk- масса корпуса, отнесенная к опоре.

Описание упругодемпферной опоры ро-

1 2 3 4 5 6

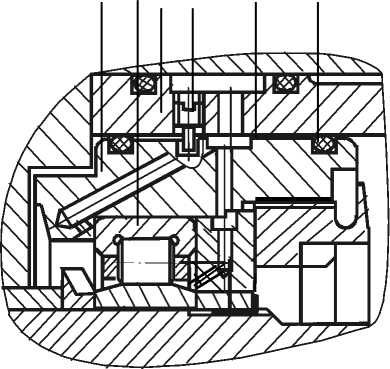
Рис.2. Конструкция передней опоры свободной турбины изделия НК-12СТ с гидродинамическим демпфером: 1 - втулка-вибратор;

2 - подшипник качения;

3 - втулка статора;

4 - штифт;

5 - радиальный зазор;

6 - упругие кольца - вторичные уплотнения тора моделью Зенера позволяет учесть податливость подшипника качения. При этом принимаем же сткость радиального подшипника линейной, с коэффициентом жесткости с2, суммарную жесткость и диссипацию демпфера с упругим элементом будем характеризовать коэффициентами же сткости с1 и демпфирования b 1. Использование ГДД в качестве демпфирующего устройства вносит суще ственную нелинейность же стко стных и демпфирующих характеристик в опору ротора при больших амплитудах колебаний. Для решения задачи динамики в линейной постановке введем ограничения по амплитуде колебаний в демпфере в виде (хд - хк)/8 < 0,4, так как в этой области жесткостные и демпфирующие характеристики в ГДД практически линейны [1]. Упругую подвеску корпуса двигателя, пренебрегая демпфированием в ней, представим в виде элемента Гука с коэффициентом жесткости с3.

Жесткость радиально-упорных подшипников нелинейно растет с увеличением отношения осевой и радиальной нагрузки [5], поэтому при эксплуатации она значительно превышает жесткость демпферов в опорах роторов ГТД. В этом случае упругий элемент с2 стремится по своим свойствам к жесткой стойке, и модель Зенера имеет предельный переход к модели Кельвина.

В случае представления опоры в виде модели Зенера систему ротор-корпус представим в виде двухмассовой с релаксационным демпфированием (рис.За). В данной модели можно получить АЧХ для ротора в опоре х р = f ( to ) втулки-вибратора демпфера х_д = f_d ( to ) и корпуса x k = f k ( to ). Для построения расчетных зависимостей необходимо составить уравнения колебаний системы релаксационного демпфирования (СРД) под воздействием возбуждающей силы F_a = A to ² sin tot :

• — m_px_p + K( ^ю )( x_p — x k ) = Ato ² sin tot ;

• - m k x k + c з x k = K ^{( to )(} x p - x k );

⁽ c + ib _x ^{to )(} x_a — x k ) = c 2 ⁽ x p - x a ),

а)

б)

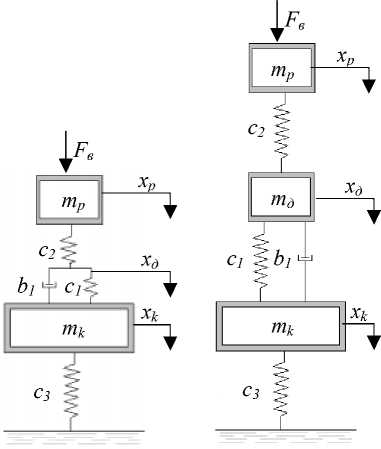
Рис.3. Схема УДО:

а - двухмассовая модель; б - трехмассовая модель

c2 (cx + ibx to)

где K(to) = ——1---1— - динамическая c 2 + c x + ibxto жесткость модели, i = V-Г.

Введем безразмерные параметры, обозначив k _x = c _x / c ₃; k ₂ = c ₂ / c ₃; M_a = m_a I m_k ;

M p = m p ¹ m k ; n = to I to k ; Q = ( c x / b x )/ to k ;

^to k = V ^c 3 / m k .

Применив метод комплексных амплитуд [6], получим уравнения колебаний СРД в следующем виде:

• -    m p n ² X p + K ( n )( X p - X k ) = k n 2 , (!)

• -    mn ² X k + c з X k = K ( n )( X p - X k ), (2)

⁽ C x ⁺ ib^ ⁾⁽ X a ^- O k ) = C 2 ⁽ X p ^- X a ), ⁽³⁾ где

K ( n ) = c 3 ^to k

k _x(x - k ₂)( k ₂ Q ² + n ²) + ik _x k ₂ ² Q n Q ²(x + k ) + n²

динамическая жесткость - функция безразмерной частоты n ;

Xp, Xg, Xk - комплексные амплитуды перемещений ротора, демпфера и корпуса, соответ- ственно.

Согласно этому методу запись перемещения в комплексном виде х = Х■ еto t, позво- ляет преобразовать исходные уравнения к системе линейных уравнений.

Решив уравнения (x) - (3), найдем амплитуды перемещений ротора, корпуса и демпфера как модули соответствующих комплексных амплитуд:

X p = —V [( C(n) + x - n ²)² + D ²( n )]/ B ( n ) ■ m_k

X k = ^{A n} V[ C ²( n ) + D ²( n )]/ B ( n );

mk

X-

ä

A n² /Q ² k ₂ ² + (x + k _x - n ² ) ² + k _x ² k₂n² m^T^    B (n)[ Q ²(x + k x )² + n ²]    ^;

x po = x p ^- x k\ = — ^x- n ²pV B C ^ ; m_k

X = X - x | = An_x -n2| ______Q_+n_______ ao a k mk * ^ *Ув(n)[Q2(i + kx)2 + n2]’ где

B( n ) = [ c ( n )(1 - n ² - M p n ²) + M p n ²(x - n ²) ] ² +

+ [ d ( n )(x - n ² - M p n ²) ^{] 2} ;

C ( n ) =

k x (x - k 2 )( k 2 Q ² + n ²) Q ²(x + k x ) + n²

D ( П ) =

k i k 2 Qn

Q ²(1 + k i ) + n² •

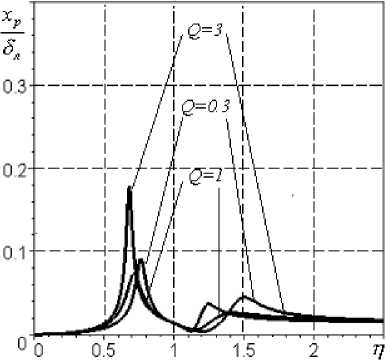
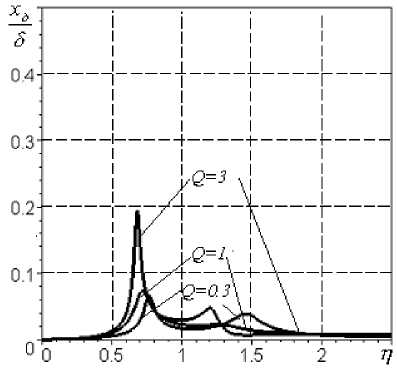
АЧХ перемещений корпуса представлены на рис.4а. Из графика рисунка видно, что абсолютные перемещения корпуса для рассматриваемой конструкции не превышают 12 мкм. Теоретические исследования желательно проводить с безразмерными параметрами, для чего представим перемещения корпуса, относительные перемещения ротора и демпфера в безразмерном виде (рис.4б, в, г, д, е). В реальных условиях сложно измерить амплитуду виброперемещения корпуса, поэтому используются лишь датчики виброскорости или виброускорения. Согласно техническим условиям виброскорость на корпусе изделия НК-12СТ при сдаточных испытаниях не должна превышать 20 мм/c. Эта величина принята за норму V_kh .

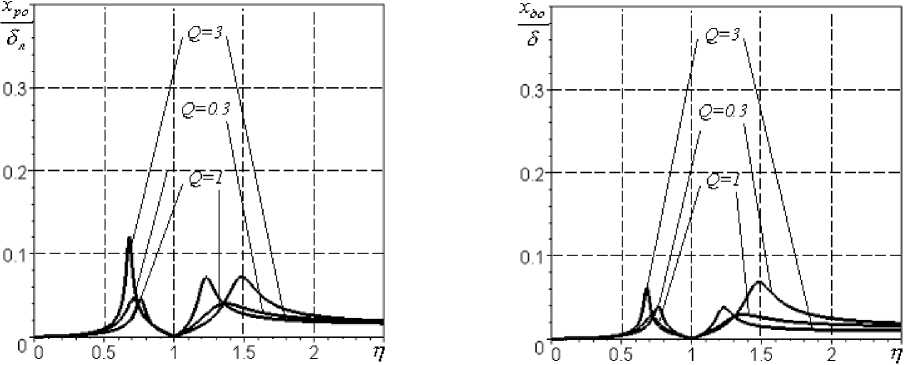
Однако, на практике ограничения накладываются на перемещения ротора относительно корпуса, что обусловлено малыми зазорами ( 8 л = 0,2...0,4 мм) в лабиринтных уплотнениях опор роторов. Кроме того, для расчета демпфирования в системе необходимо знать смещение демпфера относительно корпуса, что определяет величину параметра b ₁. На рис.4д и е показаны АЧХ перемещений ротора и втулки-вибратора демпфера относительно корпуса.

Из графиков рис.4 видно, что амплитуды колебаний ротора в опоре, демпфера и корпуса существенно отличаются при фиксированных частотах, что объясняется различием их амплитуд при собственных частотах элементов опоры.

Так как амплитуды виброускорения а , виброскорости V и виброперемещения x связаны между собой равенством a = V -p-w _k = x -n ² -w _k ², то при достижении максимума x по П в точке n ₀ для производной по частоте выполняется равенство x' ( n ₀) = 0; в то же время

V ( П 0 ) = ( x С П с ) -П 0 -^ k ) ‘ = x' ( П 0 ) -П 0 -® k +

⁺ x ⁽ П 0 ^{) -Ю} k = x ⁽ П 0 ^{) -Ю} k > ⁰ a' W =

= ( x ( П 0 > П 0 ² -® k ²) ‘ = x' ( П 0 ) -П 0 ² -® k ² +

+ 2 x ( П^По® k ² = 2 x ШПо® k ² > °.

Следовательно, максимумы x(n), V(n) и a(n) должны быть сдвинуты вправо относительно друг друга. Однако, величина таких сдвигов, как показало компьютерное моделирование, не велика.

Теперь легко получить зависимости для амплитуд виброскоростей и виброускорений ротора, корпуса и демпфера соответственно:

Vp = xpn^k, Vk = xkn^k, V = x.n^k,

ap = V'M, ak = Vkn^k, aa = VaW.

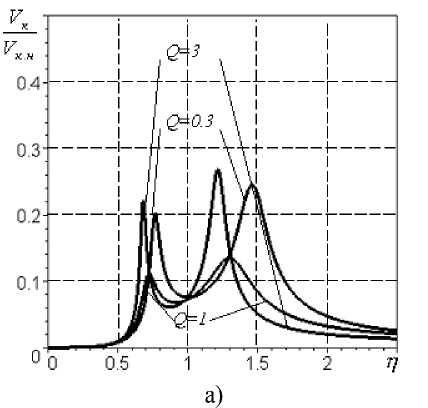
Графики АЧХ относительных перемещений, виброскорости и виброускорония ротора, демпфера и корпуса показаны на рис. 4,5.

Из анализа динамики двухмассовой системы можно сделать следующие выводы:

• 1)    на АЧХ элементов конструкции модели имеются 2 резонанса (рис.4, 5), положе -ние и величина которых определяется массово-инерционными и упругодемпфирую-щими характеристиками системы;

• 2)    увеличение жесткости демпфера c ₁ и (или) подшипника c ₂ способствует смещению резонансных частот вправо;

• 3)    увеличение удельной массы ротора M p уменьшает частотный диапазон между резонансами;

• 4)    увеличение демпфирования системы (уменьшение параметра Q ) в 10 раз для выбранных параметров снижает резонансную частоту на 15 . . 20 % (рис.4, 5);

• 5)    на АЧХ элементов конструкции модели имеются 3 инвариантные точки (рис.4), т.к. такая система является СРД (рис.3а);

• 6)    существует оптимальное значение параметра Q_onm , обеспечивающее минимальное значение амплитуд перемещений, скоростей и ускорений на резонансах;

• 7)    оптимальное значение параметра Q

опт не обеспечивает минимума амплитуд перемещений, скоростей и ускорений между резонансами;

• 8)    минимального уровня амплитуд динамических характеристик во всем частотном диапазоне можно добиться лишь путем регулирования демпфирования в системе, что позволяет настраивать систему на режим оптимального демпфирования.

Иногда масса подвижных элементов демпфера т_д (см. поз.2 на рис.2) достаточно

а)

б)

в)

г)

д)                                                        е)

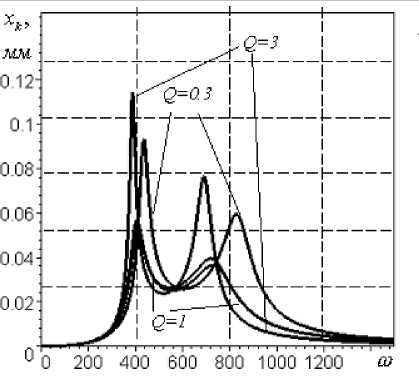
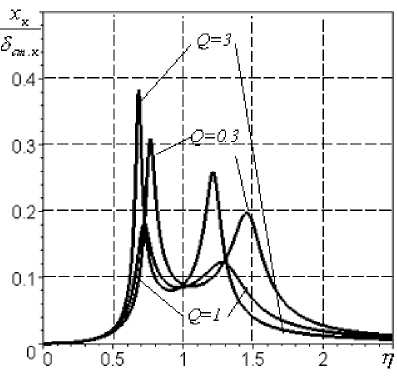
Рис.4. АЧХ перемещений при параметрах m k =400 кг; т р =150 кг; ® _k =570 c^-1; к 1 = к 2 =0,5; А =40 г - см;

8 = 0,15 мм; 8 л = 0,2 мм; 8 ст к = 30 мкм: а,б - корпуса, в - ротора, г - демпфера, д - ротора относительно корпуса, е ě демпфера относительно корпуса

б)

в)

г)

д)

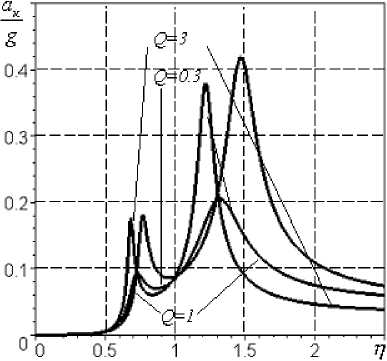
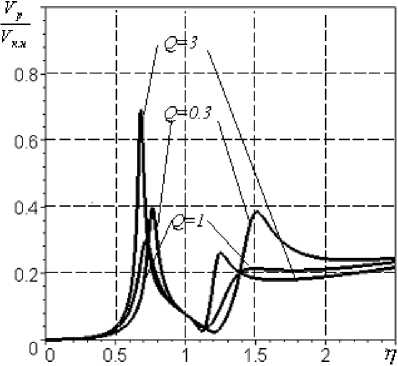
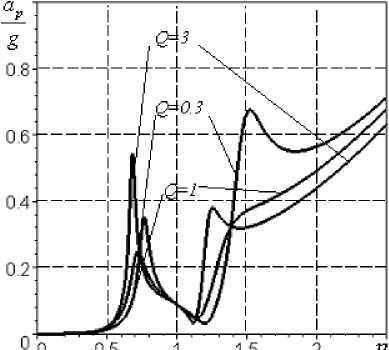
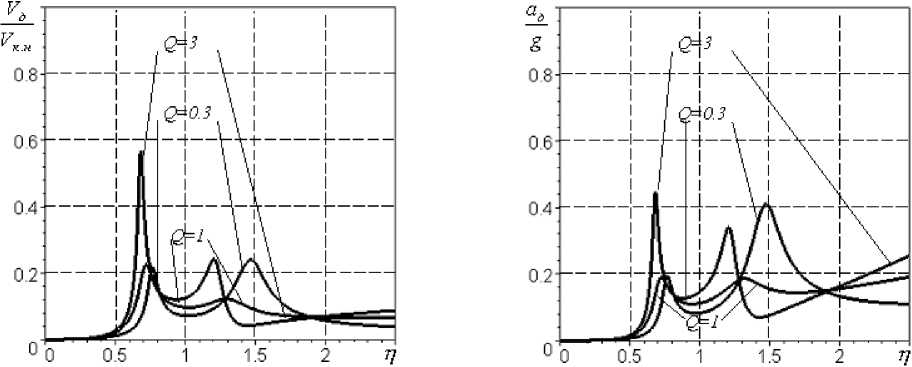
е)

Рис.5. АЧХ при параметрах mk=400 кг; тр =150 кг; wk=570 c-1; k 1=k2=0,5; A=40 г-см; Vkh= 20мм/с: а ě виброскорости корпуса, б ě виброскорости ротора, в ě виброскорости демпфера, г ě виброускорения корпуса, д ě виброускорения ротора, е ě виброускорения демпфера большая. Например, в рассматриваемой конструкции передней опоры свободной турбины тд = 17кг. В этом случае модель системы следует преобразовать в трехмассовую (рис.3б). Такая модель состоит из масс ротора mp, демпфера тд и корпуса mk, упругих элементов с жесткостями подшипника с2, слоя смазки рабочего тела демпфера с1 с коэффициентом сопротивления b 1 и корпуса c3. Уравнения движения трехмассовой системы можно представить в виде

- М р П ² X p + k ₂( X p - X_a ) = ( А / m k ) n ²; (4)

- M д П ² X д + к 1 (1 + in / Q )( X д — X k ) +

+ к 2 ( X д - X k ) = 0;                   (5)

- n ² X k + к 1 (1 + i n / Q )( X k - X_a ) + X k = 0 . (6)

Из уравнений (4) - (6) получим амплитудно-частотные характеристики перемещений аналогично тому, как это было сделано для решения уравнений (1) - (3):

x = A n² [ Q ²( ( k 2 - M д П ²)(1 + k 2 - П ²) + k 1 (1 - П ²) ) ² + p m k + + k²n² ( k 2 - M д П ² + 1 - П ² ) ²]/ G( П )          ;

x_a = — V [ Q² k 2 ²(1 + k 1 - n ²)² + k 2 k 2 n ²]/ G ( n ); m_k

X k = — V [ k 1 ² k 2 ²( Q ² + n ^!)]/ G(n) ;

mk x„ = X -Xkl = — k2Q21 -n2|/VG5); mk xpo = xp - xk| =

A n² _Q 2 1 - ₂| { k 1 + k 2 - M n ²(1 + k 1 /(1 - n ²))]² + m k         ⁷¹ F [ k 1 n /[ Q (1 - n ²)](1 - M д П ²)]²}/ G ( n )

где

' k 1 ( ^k 2 ^- M p n ² )(1 ^- n ² ) ⁺ (1 ^{+ k} 1 ^- n ² ) x) ²

G( n ) =

x ( M_d M p n ⁴ - k 2 M n ² - k 2 M p n ² )

' ⁽ k 2 ^- M p n ² )^{(1 -} n ² ) ⁺           '

+ MM n ⁴ - kM n ² - kM n ² д p ■          2 д ■          2 p ■

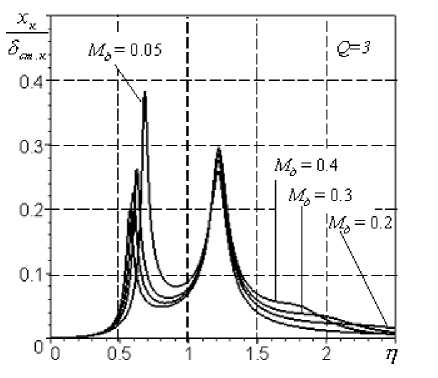
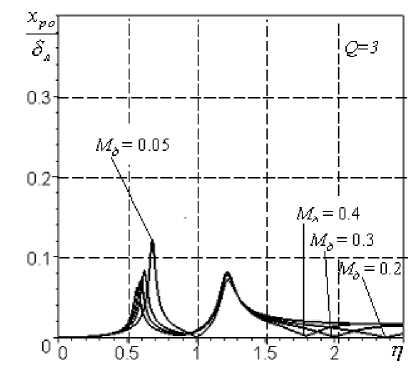
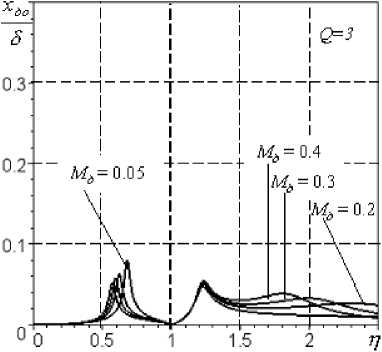
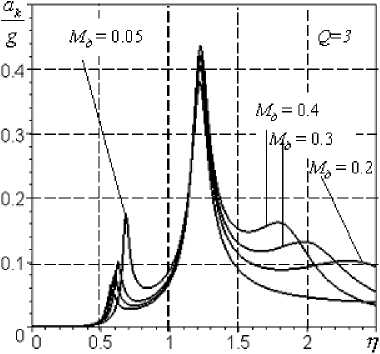
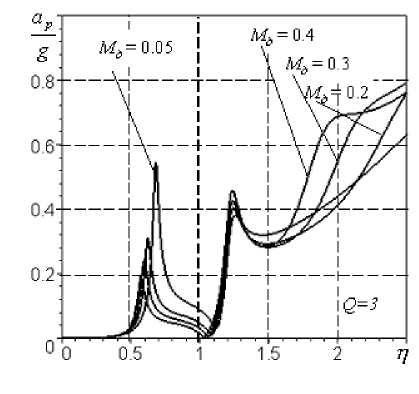
На основании этих зависимостей построены графики (рис.6), характеризующие динамику трехмассовой СРД.

Из анализа динамики трехмассовой системы можно сделать следующие выводы:

• 1)    на АЧХ виброперемещений ротора, демпфера и корпуса существуют три резонанса (рис.6а, б, в);

• 2)    наличие, величина и положение третьего резонанса зависят от массы демпфера, причем, с уменьшением массы демпфера третья собственная частота увеличивается, а резонансная амплитуда уменьшается;

• 3)    для рассматриваемых параметров модели при удельной массе демпфера М_д < 0,05 ее влияние на систему становится достаточно малым, и трехмассовую модель можно рассматривать как двухмассовую;

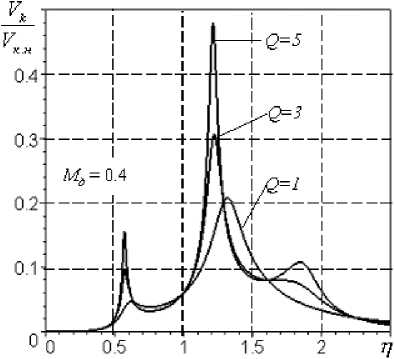
• 4)    при увеличении демпфирования (уменьшении параметра Q ) третий пик сглаживается и исчезает (рис.6г), что обусловлено тем, что демпфирующий элемент не связан с корпусом через релаксационную пружину, ослабляющую его действие, и демпфер превращается в жесткую стойку, т.е. при больших значениях демпфирования ( Q < 1) даже при большой удельной массе демпфера М_д > 0,1 систему можно моделировать двухмассовой СРД;

• 5)    на АЧХ элементов конструкции трехмассовой модели инвариантных точек нет, т.к. при представлении системы в таком виде она утрачивает релаксационную связь.

Предложенная методика расчета сложной динамической системы ротор-опора-кор-пус с помощью многомассовых реологических моделей позволяет определять динамические характеристики системы и оптимизировать ее параметры на ранних этапах проектирования.

Для оценки достоверности разработанной методики расчета динамики опорного узла ротора проведем сравнение теоретических АЧХ (рис.7) с замеренными значениями виброскорости на корпусе передней опоры свободной турбины при специальных испытаниях с дисбалансом ротора А =220 г - см изделия НК-12 СТ с гидродинамическим демпфером [7].

Жесткости с 1 - упругого элемента в виде двух колец, изготовленных из стального многожильного троса, с₂ - опоры ротора и с 3 - под-

а)

б)

в)

г)

д)

е)

Рис.6. АЧХ при параметрах m k = 400 кг; т р = 150 кг; to _k = 570 с¹;

к 1 = к2= 0,5; А=40 г-см; 8 = 0,15 мм; 8л = 0,2 мм; 8ст к = 30 мкм; VKH = 20мм/с: а - перемещения корпуса, б - перемещения ротора относительно корпуса, в - перемещения демпфера относительно корпуса, г - виброскорости корпуса, д - виброперегрузка корпуса, е - виброперегрузка ротора вески свободной турбины в районе передней опоры определялись опытным путем перед проведением испытаний. В процессе расчета значения жесткостей принимались равными соответственно с1 = 39 МН/м; c2=51 МН/м; c3=110 МН/м.

Анализ режима работы ГДД в передней опоре свободной турбины изделия НК-12СТ [8] показал, что течение смазки в демпферном зазоре ламинарное, силы инерции пренебрежительно малы по сравнению с силами, обусловленными вязкостью смазки, но на резонансных режимах работы возникает разрыв пленки смазки. Коэффициент демпфирования в этом случае для ГДД при выбранных геометрических параметрах может принимать значения в интервале Ь 1 =55.. .110 кНс/м.

Масса корпуса m_k= 386 кг и ротора т р = 152 кг, приходящиеся на переднюю опору, определялись методом приведения из условия, что вся масса свободной турбины, согласно паспортным данным на изделие, 865 кг, а ротора 170 кг. Масса подвижной части демпфера т д = 17 кг, что обеспечивает значение параметра М д <0,05 и возможность использования двухмассовой модели системы. Для выбранных значений, характеризующих динамическую систему, диапазон изменения параметра Q =0,7^1,3. Проведенные исследования динамики опорной системы с данными, подобными приведенным выше, показали (рис.5), что для нее оптимальное значение параметра Q =1,0. Это подтверждается экспериментальными данными (рис.7), так как АЧХ для значения параметра Q =1,0 наилучшим образом согласуется с экспериментальными точками, полученными на основании статистической обработки замеренных значений виброскорости.

Следовательно, разработанные методики расчета АЧХ двух- и трехмассовых систем являются вполне адекватными реальным динамическим процессам, происходящим в опорных узлах турбомашин, и могут быть рекомендованы для использования при их проектировании.

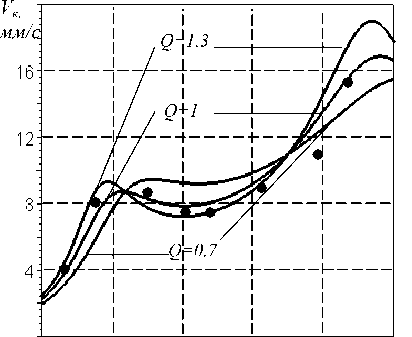
⁰ 400 500    000    700    800     Ф с"

Рис.7. АЧХ виброскорости на корпусе свободной турбины изделия НК-12СТ: ---- - теоретические кривые;

• - экспериментальные значения