Исследование собственных функций краевой задачи с нелокальными граничными условиями

Собственные значения и собственные функции - это важнейшие понятия в линейной алгебре и математическом анализе. Они играют ключевую роль в решении многих задач, связанных с линейными операторами и дифференциальными уравнениями. На основе этих понятий в различных областях науки и техники строится множество конструкций, встречающихся при моделировании реальных физических процессов.

С помощью собственных значений и собственных функций можно определить поведение системы во времени и прогнозировать ее будущее состояние. Многие соотношения, которые связаны с линейными операторами, значительно упрощаются в системе координат, построенной в базисе из собственных векторов оператора. Множество собственных значений линейного оператора, или же спектр оператора, характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат.

Краевые задачи на собственные значения для оператора Лапласа с классическими граничными условиями хорошо изучены и подробно описаны во многих учебниках и пособиях. Но некоторые свойства собственных значений, существенные для приложений, не удается получить, оставаясь в рамках традиционных граничных условий I, II и III рода. Среди прочих, к ним относится задача о максимизации разности между первым и вторым собственными значениями, возникающая в квантовой термодинамике, поставленная Виктором Павловичем Масловым во время исследования явлений сверхтекучести и сверхпроводимости [1, 2], а также возникающая в численных методах, при исследовании разностных схем [3], а также электромагнитной задаче дифракции [4, 5] на проводящих тонких экранах в постановке, описанной в [6]. Исследование асимптотики решений соответствующих операторов [7] играет важную роль в решении таких проблем, как теория самосогласованного поля в квантовой и классической статистике, сверхтекучесть и сверхпроводимость [8], квантование солитонов [9], квантовая теория поля в сильных внешних полях. К этим задачам может быть применен подход, связанный с подбором граничных условий специального типа [10].

Материалы и методы исследования. В данной статье будет рассмотрено решение система уравнений следующего вида

-y"(x) - Ay(x) = 0,x e (a,b);

’- y'(a) - r 2(a y (a) + вУ (b ))a = 0;                       (1)

_y'(b) - r 2(a y (a) + ^y (b)) в = 0, где y(x) - неизвестная функция, A - спектральный параметр, r – вещественный параметр, а, в — заданные постоянные.

Необходимо найти собственные значения A задачи (1) и соответствующие им собственные функции. Определить характер их изменения при изменении параметра r .

В рамках работы используются пары значений ( а ,в): (3,4), (-3,4). Задача решается на промежутке a = 0, b = 1 .

Рассмотрим решение задачи в общем виде. Существуют три случая: A >  0, A = 0, A <  0 .

При значениях A >  0 решение задачи (1) имеет вид:

y (x) = A sin( -Axe) + B cos(A-x),

где A, B - произвольные числа, далее будем полагать A ² + B ² ^ 0 .

Тогда краевые условия задачи (1), с учетом подстановки a = 0, b = 1, примут вид:

A ( - \/~A - a^ r ² sin ( А)) - Br ²( a + fi cos ( Aj)a = 0;

< A(Acos(A) - в2 r2 sin (A)) +

+B(-Asin(A) - r2(a + ficos(А)') в = 0.

Найдем детерминант матрицы системы (3). Также проверим, чтобы выполнялось условие совместности, то есть равенство нулю детерминанта матрицы данной системы, получаем следующее уравнение для поиска собственных значений исходной задачи:

A(2afir2 + (a2 + ^2) r2 cos (A") + A sin( A) = 0.

В случае A = 0 уравнение для поиска значения параметра r , соответствующего нулевому A примет вид

(в + a)2 r2 = 0.                                    (5)

В случае A <  0 рассуждая аналогично случаю A >  0 , приходим к уравнению, решение которого определяет отрицательные собственные значения:

V -A(2aPr2 + (a2 + в2) r2 ch (V-A) - V -Ash (4~A)) = 0.           (6)

Результаты и их обсуждение. Рассмотрим решение задачи для α(+). Подставим значения (3, 4) и a = 0, b = 1 в задачу (1), а также уравнения (4) и (6), получим:

- y" ( x ) - I y ( x ) = 0, x е (0,1);

<- y '(0) - r 2(3 y (0) + 4 y (1))3 = 0;

y '(1) - r 2(3 y (0) + 4 y (1))4 = 0, r2(24 + 25cos (VI)) = - Ц sin( U),(8)

r2(24 + 25ch (V-I)) = 4-lsh (V-I).(9)

Найдем первые три собственных значения I при различных значениях параметра r. При увеличении значения параметра r происходит уменьшение первого собственного значения.

При          малых

r2 I ^ 0,1 ^ п2,1 ^ 4п2.

На рисунке 1 представлены графики I при различных значениях параметра r для данной задачи.

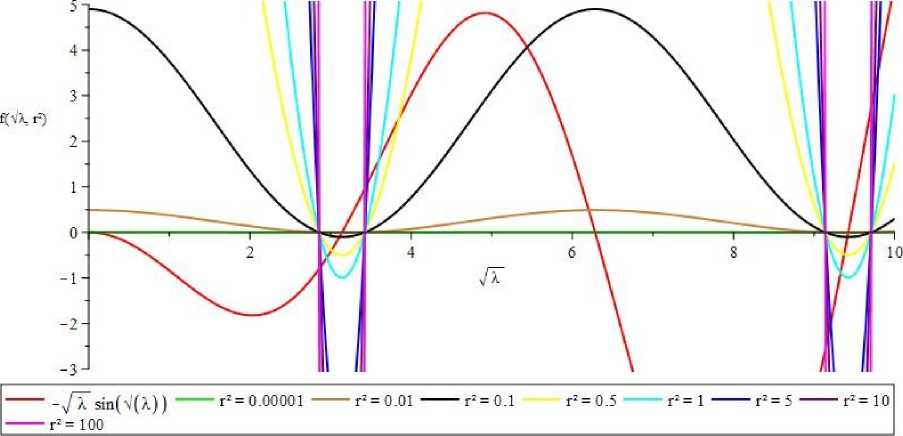
Рис. 1. Значения I при различных r для задачи а(+)

Произведем нормировку таким образом, чтобы собственные функции удовлетворяли выражению A2 + B2 = 1. Полученные собственные функции для каждого собственного значения представлены на рисунках 2,3,4 благодаря выполненной ранее нормировке, все они будут лежать в пределах полосы от -1 до 1.

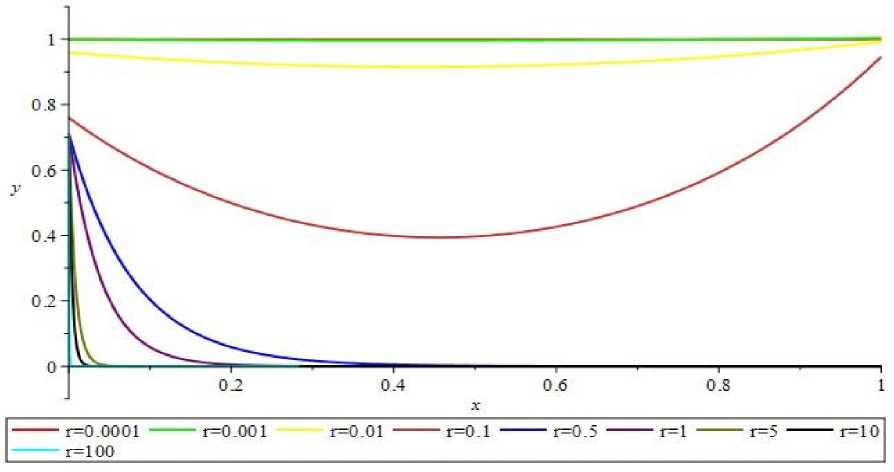
Рис. 2. Графики собственных функций при λ и различных r для задачи α(+)

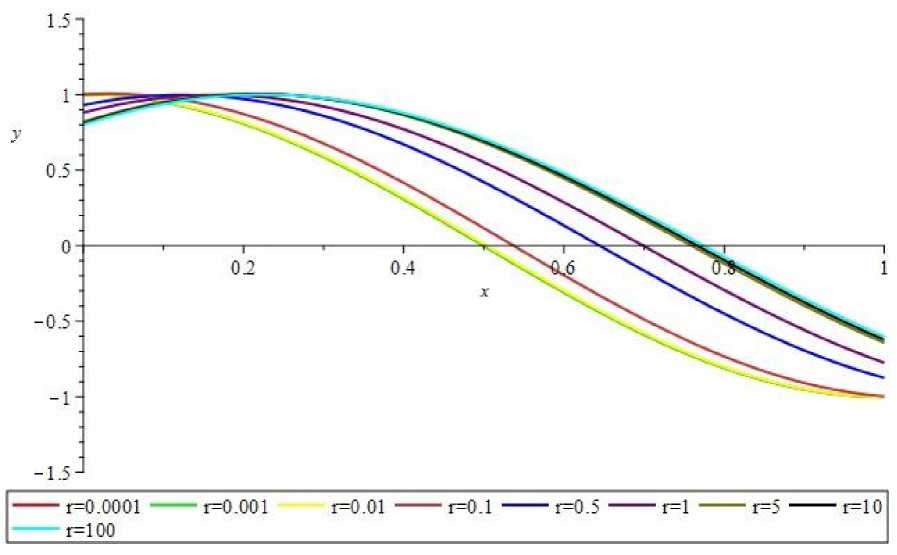
Рис. 3. Графики собственных функций при λ и различных r для задачи α(+)

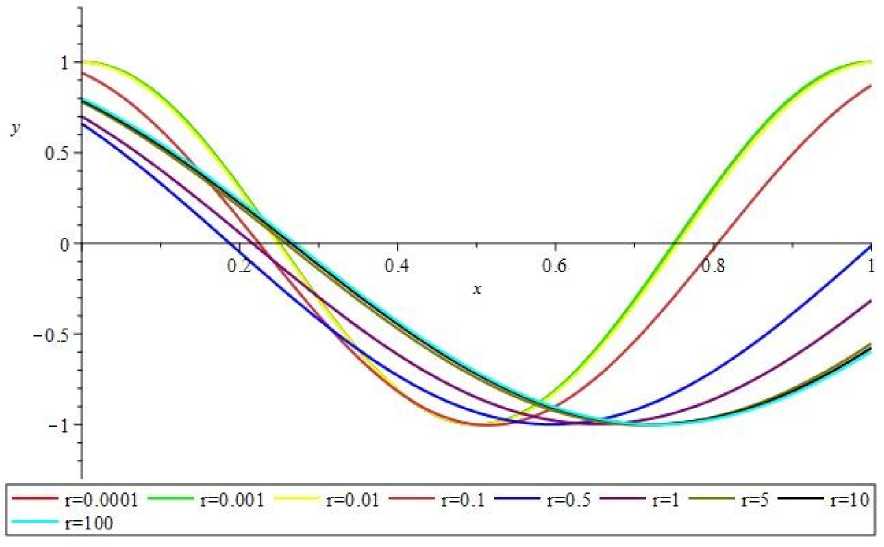
Рис. 4. Графики собственных функций при Л и различных r для задачи а(+)

Далее приведено решение задачи в случае    в задачу (1), а также уравнения (4) и (6), полу- а(-). Подставим значения (-3, 4) и a = 0, b = 1    чим:

- y "( x ) - Л у ( x ) = 0, x е (0,1);

<- у '(0) + r 2(-3 у (0) + 4 у (1))3 = 0;

у '(1) - r 2(-3 у (0) + 4 у (1))4 = 0, r2(-24 + 25cos (VI)) = - Ц sin( Ц),(11)

r2(-24 + 25ch (4-ЛУ) = j-Ash (V-I).(12)

Найдем первые три собственных значения Л при различных значениях параметра r. При увеличении значения параметра r происходит уменьшение первого собственного значения. При малых r2 Л ^ 0, Л ^ п2,1 ^ 4п2. Также отме- тим, что при росте r второе собственное значение стремится к нулю.

На рисунке 5 представлены графики Л при различных значениях параметра r для данной задачи.

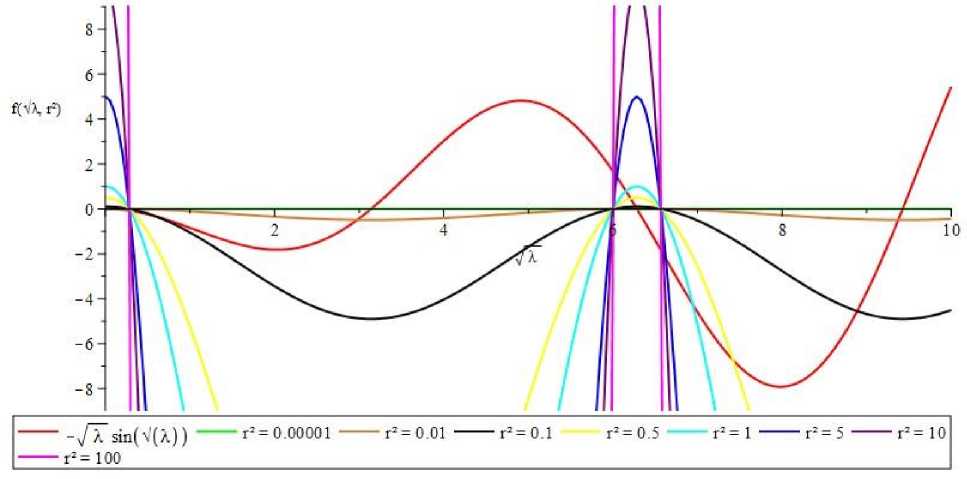
Рис. 5. Значения λ при различных r для задачи α(-)

Первая собственная функция прижимается к осям координат при больших значениях и переходит в прямую на близких к нулевым. Это поведение аналогично прошлому случаю, второе семейство собственных функций пре- терпевает характерные изменения, третья практически не меняется, только сдвигается по оси абсцисс. Графики полученных собственных функций представлены на рисунках 6, 7, 8.

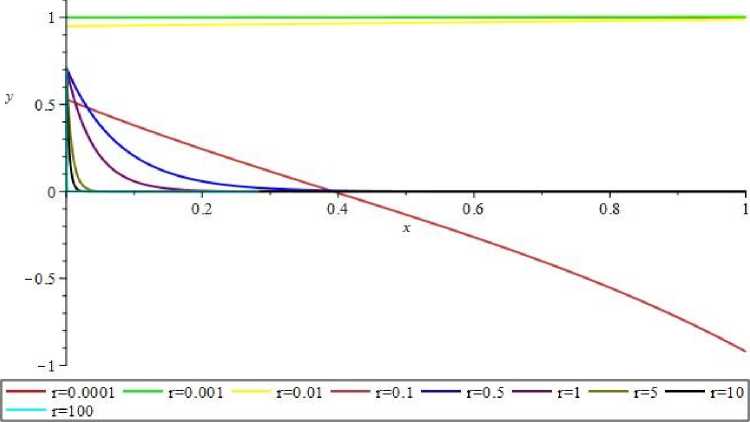
Рис. 6. Графики собственных функций при λ и различных r для задачи α(-)

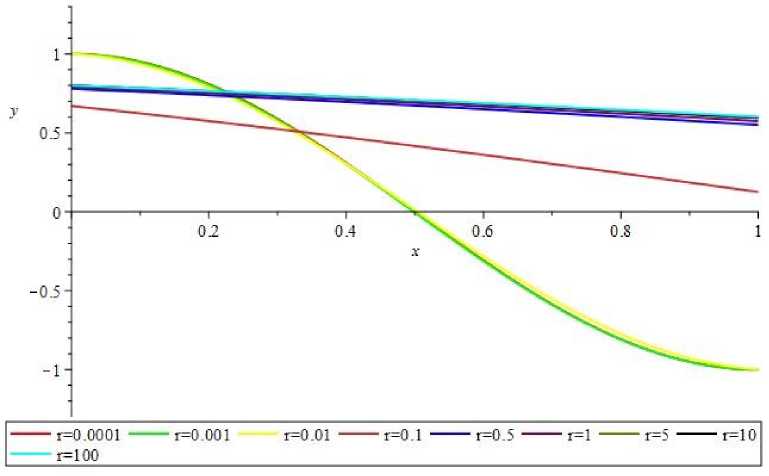
Рис. 7. Графики собственных функций при Л₂ и различных r для задачи а(-)

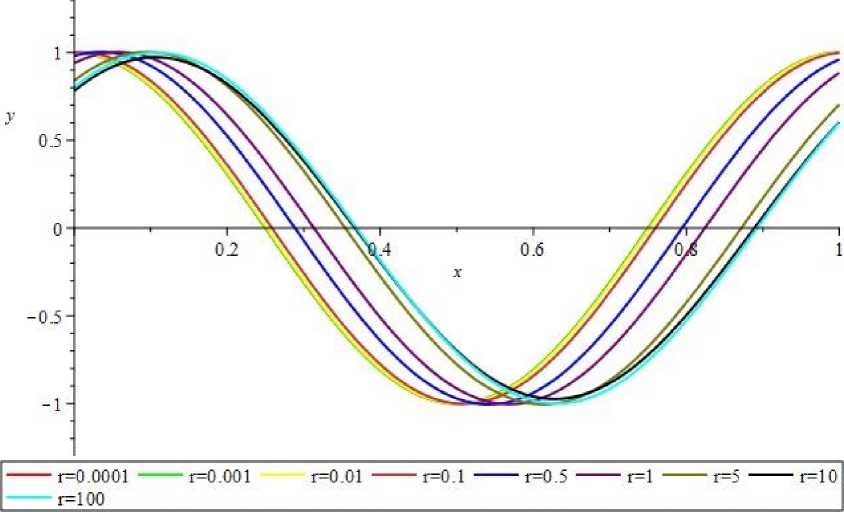
Рис. 8. Графики собственных функций при ^ и различных r для задачи а(-)

Все первые собственные значения при любых значениях параметра r получились отрица- тельными. Перепишем формулу (9) в виде

r 2( Fch (z) - G) sh (z)

где F = a2 + в2, G = 2ав. Пренебрегаем слагаемым с отрицательным знаком в экспоненте ввиду того, что собственные значения неограниченно убывают. Делим числитель и знаменатель (13) на sh(z), учитывая описанное допущение, получаем:

z = r 2( F

2G

ez

Избавляемся от слагаемого, содержащего G , как в предыдущем случае. Далее, подставляя вместо z исходное собственное зна- чение, получаем следующую асимптотическую оценку для первого собственного значения:

A <- r4 F2.

Можно определить линейный функционал и получить оценку для первого собственного значения сверху. В обоих случаях отрицательным может быть только первое собствен- ное число, все последующие значения положительны. Для задачи (1) оценка, соответственно, равна:

1 -/        - r2 Uh          2n;rf

A (rp) <-------;---r h

• 1    +      '----7r2 DV h D2

По результатам вычислений, спектр значений сверху ограничен нулем, что не противоречит асимптотической оценке при неограниченном уменьшении параметра r . Собственное значение неограниченно возрастает, а F является постоянной величиной, следовательно, вещественный параметр r должен быть неограниченно велик. По мере роста значения параметра r практические оценки все ближе к теоретическим, но при этом всегда остаются меньше них. От знака параметра α данный результат не зависит, в обоих случаях зависимость сохраняется. Следовательно, можно утверждать, что построенные оценки корректны и применимы при заданных нелокальных граничных условиях. Вырождение в вертикальные прямые, как и переходы через линейную функцию от синусов и косинусам к гиперболическим аналогам, не зависит от конкретных значений и разницы между ними. При обнулении любого из параметров α и β , как частный случай исследованных задач, мы приходим к классическим задачам с локальными граничными условиями.