Исследование сопротивления пластической деформации стали марки 32ХГА

От величины сопротивления металлов пластической деформации зависит прежде всего уровень энергосиловых параметров процесса и, следовательно, мощность, которую необходимо подвести в очаг деформации.

На величину сопротивления металлов пластической деформации влияет множество факторов, наиболее значимые из которых: тип кристаллической решетки металла, его химический состав, степень и скорость деформации, температура металла, история развития деформации во времени и др. [1]. В настоящее время известно довольно много методик расчёта величины сопротивления металла деформации [2, 3]. При этом, как правило, методики определения сопротивления металлов пластической деформации для случаев холодного и горячего деформирования различаются между собой. При холодной деформации считается, что сопротивление металла пластической деформации зависит только от степени деформации и эта зависимость имеет степенной характер. При горячей деформации широкое распространение нашел метод термомеханических коэффициентов, позволяющий учесть влияние на сопротивление металла пластической деформации степени, скорости и температуры [4]. Как правило, зависимость величины сопротивления деформации определяют отдельно для случая холодной (20–300 °С) и для горячей (800–1200 °С) деформации [3, 5–9]. Как следствие, известные методики нельзя распространить на случай теплой деформации (для сталей это диапазон температур от 300 до 800 °С) и к тому же многие из них не учитывают влияние деформации, накопленной на предыдущих производственных этапах.

Достаточно корректные и научно обоснованные методики определения сопротивления металла пластической деформации как функционала, учитывающего историю деформирования, представлены в работе [10, 11]. Однако эти методики приводят к необходимости ре- шения интегральных уравнений, что связано с существенными математическими трудностями. Поэтому в работе [11] на основе полученного функционала предложен рекуррентный алгоритм расчета сопротивления металла пластической деформации и методика определения входящих в него реологических коэффициентов. При этом, в частности, для определения скорости разупрочнения металла используется известная формула [12]

Г А t)

^Ao _s = ^Ao _s o exp I^-—I ,                (1)

к к )

где Ao 5 - величина остаточного упрочнения через промежуток времени A t после окончания процесса деформирования; Ao 5 ₀ - величина упрочнения металла в конце процесса деформации; k – эмпирический коэффициент, который характеризует скорость процессов разупрочнения и зависит от температуры металла [11].

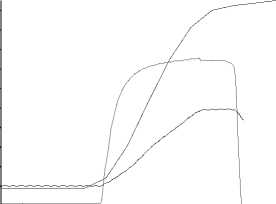
Для определения численных значений коэффициента k была проведена серия испыта- ний на комплексе Gleeble 3800. Данный комплекс в последнее время широко применяется для исследования процессов деформации [6, 8, 9, 13, 12]. Как было сказано выше, исследования проводились на трубной стали 32ХГА. Данная марка стали широко используется при производстве бесшовных труб для нефтегазовой промышленности. По результатам эксперимента для этой стали были построены кривые зависимости ее сопротивления деформации от степени деформации в диапазоне температур от 20 до 1200 °С. Для определения коэффициента разупрочнения были использованы результаты испытаний при температурах от 300 до 1200 °С, поскольку при меньших температурах разупрочнение практически не наблюдается. Кривые, описывающие зависимость величины сопротивления деформации от степени деформации для различных температур, представлены на рис. 1. Из рис. 1 видно, что с ростом температуры деформации увеличивается величина разупрочнения.

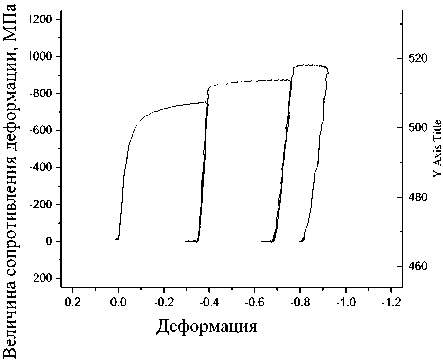
300 °С

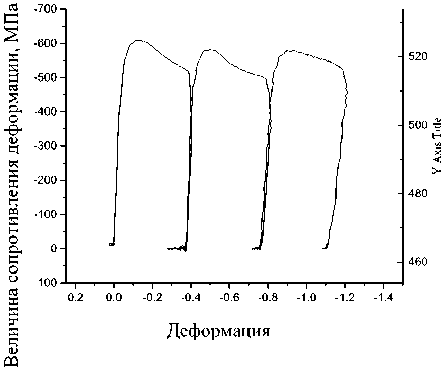
600 °С

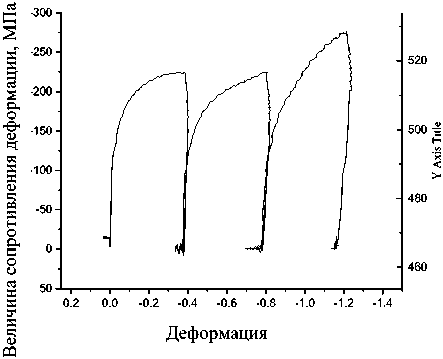
900 °С

Рис. 1. Зависимость величины сопротивления деформации стали 32ХГА от величины деформации при различных температурах

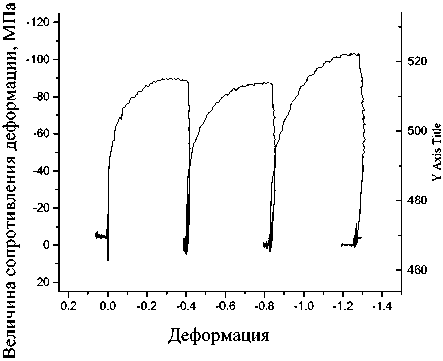
1200 °С

На основе зависимостей, полученных в результате испытания образцов на сжатие, были получены значения коэффициентов,

k = 0,0225

1395-0 ^ 0 + 20 J,

входящих в зависимости для расчета величины сопротивления деформации. Для этого

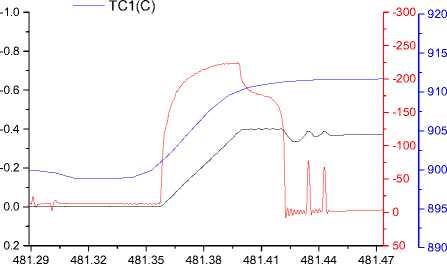
кривые изменения величины сопротивления деформации и степени деформации представлялись в виде зависимостей от времени (рис. 2).

Величина коэффициента k определялась

где 0 - температура стали.

Для обработки экспериментальных и получения значений остальных коэффициентов

использовали метод наименьших квадратов. В результате зависимость (1) для стали 32ХГА

примет вид

на основе экспериментальных данных по формуле

Ac _s = 542,266 ■ exp

A t

—

k       A t

. ACe ln S

^Ac 5 0

.

0,0225 ( 1395 —0 ^

(   ,     ( 0 + 20 ) J

.

Определить зависимость коэффициента k от температуры оказалось возможным благо-

даря системам автоматизации установки Gleeble 3800. Поскольку, как видно из рис. 2, во время разупрочнения температура металла остается практически постоянной, полученная зависимость коэффициента разупрочнения от температуры имеет вид:

Для определения влияния деформационной составляющей упрочнения на величину сопротивления металла пластической деформации были проведены эксперименты по растяжению образцов из стали 32ХГА при комнатной температуре. Эксперименты также проводились на комплексе Gleeble 3800. После обработки полученных результатов с применением метода наименьших квадратов было получено уравне-

ние, описывающее кривую упрочнения:

-1.0

Strain Stress(MPa) TC1(C)

-0.8

-0.6

-0.4

-0.2

0.0

361.32    361.35    361.38    361.41    361.44    361.47

-1000 345

-800 335

-600 325

-400 315

-0.8

-700 640

-200 305

Strain Stress(MPa) TC1(C)

-0.6

-0.4

-0.2

0.0

-300 615

-200 610

-500

-400

-100

421.47

Time(sec)

421.32   421.35   421.38   421.41    421.44

-600 635

0.2

0.2

100 590

600 °С

Time(sec)

300 °С

Strain

Stress(MPa)

-1.0

Time(sec)

900 °С

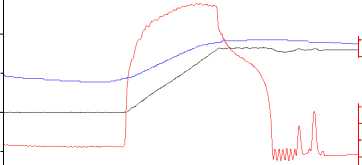
Рис. 2. Зависимости величины сопротивления деформации (–), температуры (–) и степени деформации (–) от времени

0.5

-120 1210

-100

Strain Stress(MPa) TC1(C)

0.0

-0.5

-80

-60

-40

-20

541.32

541.35

541.38

541.41

541.44

Time(sec)

1200 °С

о _s = 542,266 + 3796 Л ^0,91 , (5) где Л - величина деформации.

Для оценки адекватности полученного уравнения была построена диаграмма соответствия экспериментальных и расчётных данных (рис. 3).

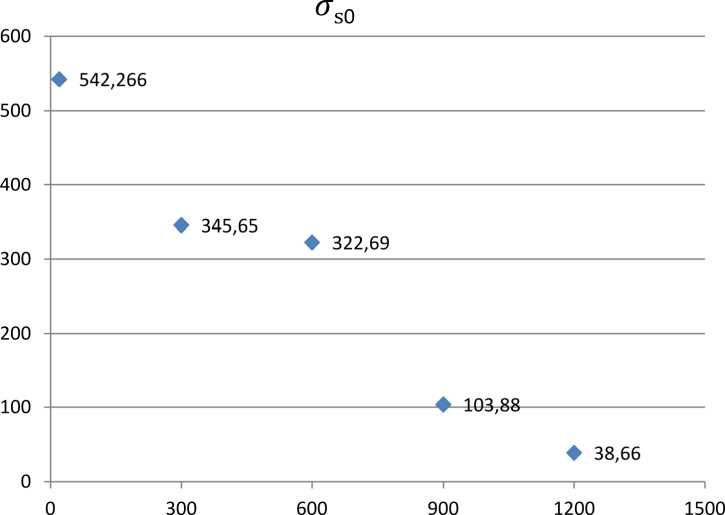
Согласно методике, изложенной в работе [11], для определения сопротивления металла пластической деформации необходимо также знать влияние температуры на сопротивление металла пластической деформации в исходном состоянии. За основу при этом была взята зависимость, общий вид которой представлен в работе [11]. Для определения эмпирических коэффициентов, входящих в эту зависимость, были проведены эксперименты по растяжению образцов при различных температурах на комплексе Gleeble 3800. Полученные экспериментальные данные представлены на рис. 4. Уравнение регрессии, построенное путем обработки полученных экспериментальных данных также с помощью метода наименьших квадратов, имеет вид о 50 = 542,266 exp

- 0,902

( 9- 20 )

1 1395 -9 о J

0.615

. (6)

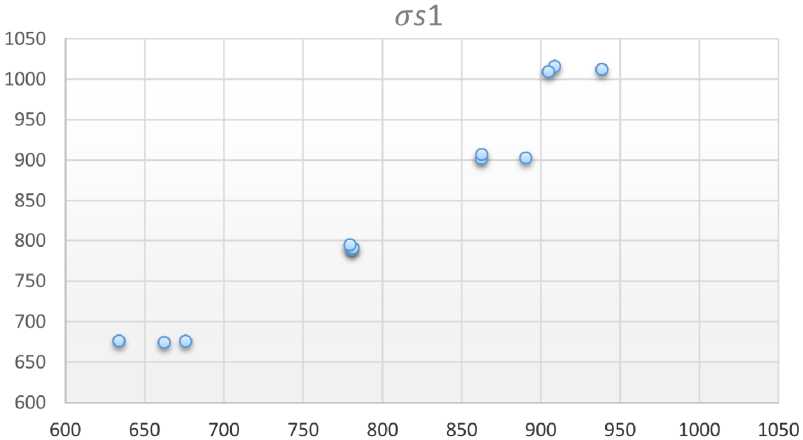
Рис. 3. Диаграмма соответствия расчетных и экспериментальных данных по определению сопротивления пластической деформации стали марки 32ХГА при комнатной температуре

е

Рис. 4. Влияние температуры нагрева на сопротивление пластической деформации стали 32ХГА в недеформированном состоянии

В итоге получено базовое уравнение рекуррентного алгоритма определения сопротивления пластической деформации стали марки 32ХГА в виде

m

ст si = 542exp - 0,902

' 0 ₀ - 20

V 1395 -0 0 )_

+№ 796 ( Л 0,⁹¹

i = 1

- Л 0,⁹¹ )

0,615

+

\

\

ct s ( . — 1 )- ⁵42exp -(W

V                 L

' 0 0 - 20

_V 1395 -0 ₀

-10,615 A

exp

^(-A t )

- 1

V

0,0225 [       ⁰ A

V , V 0 + 20 ))   )

Г (7)

Заключение

В представленной работе выполнено комплексное исследование процессов упрочнения и разупрочнения стали 32ХГА в диапазоне изменения температуры от 20 до 1200 °С. Получено рекуррентное уравнение для расчёта величины сопротивления деформации металла в диапазоне температур от 20 до 1200 °С. Определена зависимость для вычисления коэффициента разупрочнения стали.

Полученные результаты могут быть использованы при определении технологических параметров процессов холодной прокатки труб, например на станах ХПТ, трубоэлектросварочных агрегатах (температура от 20 до300 °С), процессов калибровки и правки труб в термических отделах (температура от 300 до 700 °С) и процессов горячей деформации при прошивке и раскатке гильз (температура выше 700 °С).