Исследование сопротивления связи экранирующих материалов

Основная идея оценки сопротивления связи радиочастотных кабелей триаксиальным методом заключается в создании помехонесущего поля между внешней трубой и оплеткой кабеля, в результате чего на оплетке кабеля появляется помехонесущий ток, который в свою очередь создает наводки на жиле кабеля. Замеряя разностьпотен-циалов между жилой и оплеткой кабеля, а также разность потенциалов между трубой и оплеткой кабеля, затем, беря их отношение, получаем значение для сопротивления связи тестируемого образца кабеля. При этом нужно учитыватьдополнительные поправочные коэффициенты, связанные с неоднородностью распределения тока в системе. Сопротивление связи является одним из основных параметров для определения эффективности экранирования [1]. На основе триаксиального метода создаются и эксплуатируются измерительные установки [2].

Теоретические исследования эффективности экранирования радиочастотных кабелей выражаются в формулах, на основе которых возможен расчет экранов различных конструкций. Однако полученные формулы являются приближенными и не могут применяться на практике для оценки помехозащищенности кабеля (кабельных систем). Точный расчет несплошных экранов связан с большими трудностями. При этом особое значение приобретают экспериментальные методы оценки эффективности экранирования.

При построении триаксиальной измерительной системы за основу была взята принципиальная схема (рис. 1), примененная в работе [3].

Распределения токов и напряжений вдольпроводни-ков триаксальной установки описываются с помощью телеграфных уравнений. Измерительную систему можно разбитьна две цепи: внешнюю, образованную внутренней поверхностью трубы и внешней поверхностью экрана и внутреннюю, образованную жилой и внутренней поверхностью экрана. При этом в отличие от [3], где система работает в согласованном режиме, в изложенных ниже математических выкладках учитывался случай, ког- да внешняя и внутренняя цепи не имеют хорошего согласования. Такой случай имеет практическую значимость при исследовании различных кабельных оплеток, не входящих в состав готового кабеля со стандартным волно- вым сопротивлением.

В установившемся режиме телеграфные уравнения для внешней цепи записываются следующим образом [4]:

⎧ dV_T ⎪ dx _⎪ dI_Т ⎪⎩ dx

- Z_ТI_Т ;

- Y Т V Т ,

где V_Т и I_Т – соответственно напряжение и ток во внешней цепи; Z_Т = R_Т + j ω L_Т , где R_Т , G_Т – соответственно погонные сопротивление и индуктивность внешней цепи;

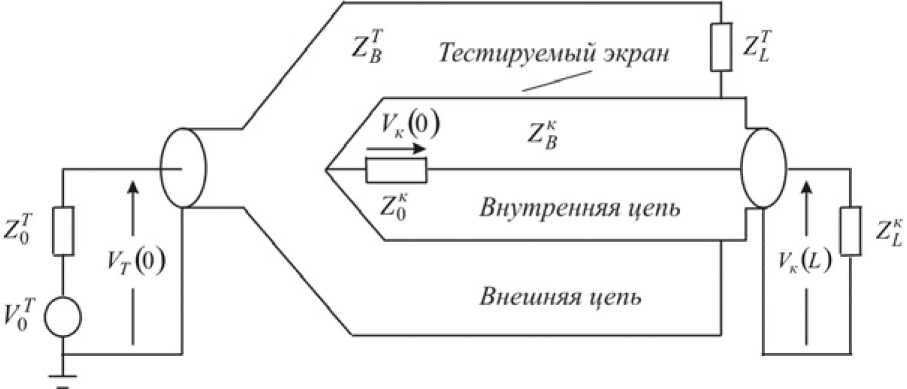
Рис. 1. Схема триакисальной линии

Y_T = G_T + j to C^ где G_T С Т - соответственно погонные проводимость изоляции и емкость; to - циклическая частота тока; j – мнимая единица. Решение уравнений (1) можно представитьв виде суперпозиций гиперболических функций:

У_т - V_T ( 0 ) ch у _Tx - Z j l_T ( 0 ) sh у _Tx ;

I = I ( 0 ) ch у x —2- Г ( 0 ) sh у x .       ⁽²⁾

[ Z B

Здесь у t = Z/.Y , Z_B^r

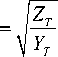
. Граничные условия для внешней цепи рассматриваемой установки имеют вид

V ( 0 ) - Vт - Z T I t ( 0 ) ;

К ( l ) - Z T I t ( l ) ,

где V0Т – выходное напряжение генератора, прикладываемое к внешней поверхности оплетки и внутренней поверхности трубы; L – длина кабеля. Применяя условия (3) к решениям (2), получаем следующие выражения для констант интегрирования:

V T ch у_т L +    V sh у_т L

0 ТТ 0 Т

It (0)  -----------ZTZT-----Z;

Z T ch у _T L +— ^{, 0} sh у _T L + Z T ch у _T L + Z T sh у _T L ВТ   _ZВ Т   Т     ТВТ

V (0)-          VZ ch у tL + Z^VT sh уtL,

Z T ch у _T L + ^L ^0 sh у _T L + Z T ch у _T L + Z T sh у _T L

L             ZВ              0

которые для согласованной линии преобразуются к виду vT

I T ^{( 0 )}- .<^;

V s ( 0 ) - V T .

Напряжение и ток на дальнем конце внешней цепи зи; Y- проводимость связи. Решение уравнений (9) выглядит следующим образом:

' V k ( x ) - V k ( 0 ) ch у , x - Z B I_K ( 0 ) sh у , x + V к ( x ) + I T ( x ) ;

[ Ik (x) - Ik (0) ch у kx - Vk (0) sh у ,x + V (x) +1В (x). (10) ZB к    Zк

Здесь у к ^- Z/Y- ; Z^B Y_y^ ;

x

Vk (x)- Zсв J It (^) ch у к (x -^) d ^;(11)

• IT( x )-- Y„ ZB J Vt (^) sh у к (x -^) d ^;(12)

x

V (x )-- -k J It (5) sh у к (x-^) d ^;(13)

Z_{В 0}

x

IВ (x)-ZBY„ J It (5) ch у к (x-^) d^ .(14)

Граничные условия для внутренней цепи формулируются следующим образом:

V ( 0 ) -- Z X ( 0 ) ;

[ V, ( L ) - Z^I, ( L ) .                    ⁽¹⁵⁾

Подстановка решений (10) в (15) дает выражения

^Vк ( ^L ) + I T ( ^L ) - Z I V T ( ^L ) - Z L I В ( ^L )

I, ^{( 0 )}  ----------------------------------- k^-k -------; ⁽¹⁶⁾

Z к ch у k L + Z B sh у k L + Z k ch у k L + -L Z⁰- sh у k L

ZВ

V k ( 0 ) -- Z k X

• V T к ( ^L ) + I T^k ( ^L ) - ^Zk^VT^k ( ^L ) - ryВ ( ^L )         ₍ к

^X                                    T k/k       . ⁽¹⁷⁾

Z к ch у k L + Z B sh у k L + Z k ch у k L + -^^ sh у k L

ZВ

Для согласованной внутренней цепи (16) и (17) преобразуются к более простому виду определятся аналогичными выражениями:

vT

V t ( L ) - ^ IT ( ^L ) - _{; /} ^

Таким образом, решение телеграфных уравнений, удовлетворяющее граничным условиям (3) для согласованной внешней цепи записывается следующим образом:

I _{( 0} ) = VВ ( L ) + I t ( L ) - ZkV; ( L ) - ZkI-k ( L ) ^kl ’           2 ZB (ch у L + sh у kL )          ^;

^Vk ( ⁰ ) = -

V; ( L ) + IT ( L ) - ZV ( L ) - ZkIk ( L ) ² ( ^ch у k^{L + sh} у k^L )

Подставляя (18) и (19) в (10), получаем

^Vt ( x ) = <

I T ^{( x} ) ^-

V

( ch у _T x - sh у _T x ) ;

V

2 Z ( ^ch у T^{x - sh} у T^x ) .

Телеграфные уравнения, связывающие ток I и напряжение V внутренней цепи с учетом проникновения электрического поля внешней цепи, а также с учетом наведенных магнитным полем внешней цепи токов, можно

^ ^X( ^ch у k^{x + sh} у k^x )⁺ V ( ^x )⁺ I T ( ^x ) ;

' I (x. = Vkjk)±Iтxk)zzVjk)zzk/вjk)x k                 2 (ch у kL + sh у kL)

x ( ch у _kx + sh у _kx ) + V_T ^k ( x ) + I k ( x ) .                    ⁽²⁰⁾

представитьв виде

' dV dx

' dk , dx

: - Z I + Z I' кк св ;

- YV + YV , кк св

Из уравнений (20) можно получить выражение для определяемой на опыте разности потенциалов между жилой и экраном на конце кабеля:

V k ( L ) - 2 ( V в ( L ) + I t ( L ) + Z k V T ( L ) + Z k I T ( L ) ) . (21)

где Z = R + j to L , где R , G - соответственно погонные сопротивление и индуктивность внутренней цепи; ¥_к = G_k + j to C_k , где G_k , С к - соответственно погонные проводимость изоляции и емкость; Z св - сопротивление свя

Производя интегрирование в (11)–(14), получаем

V k ( ^L ) - 2 2 k V ^T x

х(у т sh у tL-у к sh у kL ) + у т (ch у kL - ch у tL ).     ( у T-ук                      ’

×

I ^ˆ Т ^к ( L ) = Z В ^кY св ×

V ₀ ^Т γ _к ( ch γ _к L - ch γ _Т L ) -γ _Т sh γ _к L +γ _к sh γ _Т L

^γ Т ² V ˆ Т^к ( L ) = ^{Z с}

-γ _к ²

;

где r _Т – радиус трубы, r_о – радиус экрана, r _ж – радиус жилы, ε _и^Т_з – диэлектрическая проницаемостьизолятора, заполняющего пространство между трубой и экраном, ε ^к_из – диэлектрическая проницаемостьизолятора кабеля,

св Т

2 V 0 ^×

μ ₀ =1, 257⋅10

-

^{6 м ⋅ кг} ε=8,85⋅10 ^{- 12 сА} , 0

с2А2                    м3 ⋅ кг

.

_× γ _к sh γ _ТL -γ _Т sh γ _кL +γ _к ( ch γ _кL - ch γ _ТL )

.

γ _Т -γ _к

I ^{ˆ к} L = Y^{V 0} ×

В         св 2

_× γ _Т sh γ _Т L -γ _к sh γ _к L +γ _Т ( ch γ _к L - ch γ _Т L )

22 γ _Т -γ _к

.

Подставляя теперь(22)–(25) в (21), имеем при условии согласования волновых сопротивлений внешней и внутренней цепей выражение

V к ( L ) = ¹ V 0 ^Т γ _Т

-

⎛Z        ⎞ св +ZТY ×

В св γ к ⎝ Z В ^Т        ⎠

× ( ch γ _к L - ch γ _Т L + sh γ _Т L - sh γ _к L ) .

В рассматриваемом случае коэффициентами затухания α _к , α _Т можно пренебречьпо сравнению с коэффициентами фаз β _к , β _Т ( γ _Т = α _Т + j β _Т , γ _к = α _к + j β _к ). В связи с этим выражение (26) перепишется следующим образом:

V к ( L ) = ¹ ₄ V 0 ^Т _{j β Т}

-

⎛Z        ⎞ св +ZТY ×

⎜Т        Всв⎟ jβк⎝ZВ        ⎠

× ( ch j β _к L - ch j β _Т L + sh j β _Т L - sh j β _к L ) .       (27)

Отделяя в (26) вещественную частьот мнимой, получаем

V к ( L ) = ¹ ₄ V 0 ^Т _{β Т}

-

⎛⎞ св Т

⎜ _Т + Z _В Y _св ⎟×

^β к ⎝ Z В        ⎠

j ( cos β _Т L - cos β _к L ) ) .

На опыте измеряется абсолютная величина выражения разности потенциалов. Поэтому необходимо вычис-литьмодульвыражения (28).

Vк (L)=1

VT

z свТ 4(βТ-βк)⎝ZВТ+ZВYсв

×

× ( sin β _кL - sin β _ТL ) ² + ( cos β _ТL - cos β _кL ) ² . После простых преобразований получаем

Vк ( L ) ₌ 1 ⎛ Z с

_sin ( β к -β Т ) L

VT

V ₀

2 ⎝ Z

^⎞ 2_. ^{св ⎟}⎠ ( β к -β Т )

Аналогично для напряжения на ближнем конце кабеля имеем формулу

V к ( 0 ) = ^{1 ⎛ Z св} - Z^ТY Т ⎜ ТВ св

V ₀     2 ⎝ Z_В

_sin ( β Т +β к ) L

2 ( β Т +β к ) ^.

Фазовые постоянные выглядят следующим образом:

β _Т =ω

где to = 2 n f, / - частота сигнала. Ниже записаны выражения для емкостей и индуктивностей:

= ^{μ 0} ln ^{r Т} ; L к

СТ

2 π    r_о

2πε εТ

= 0из ln rТ rо

к

= ^{μ 0} ln ^rо ;

2 π   r _ж

;

Ск =

^к 2 πε ₀ ε _из

, ln rо rж

С помощью этих выражений для фазовых постоянных окончательно имеем

β _Т =ω μ ₀ ε ₀ ε ^Т _из , β _к =ω μ 0 ε 0 ε из .

Тогда сопротивление связи определится следующим образом:

7 = 27

Z _св = 2 Z_В

V к ( L ) г

^V 0 ^Т sin

- ( Z В^Т ) ² Y св . (34)

Поскольку измерения проводятся для сравнительно низкого диапазона частот (до 100 МГц), второе слагаемое в (34) можно отбросить. Как пример, рассмотрим случай, когда пространство между кабелем и трубой заполнено воздухом, тогда из (34) следует формула

7 = TZT

Z _св = 2 Z_В

V к ( L )

V0Т sin

L

При отсутствии хорошего согласования волновых сопротивлений внутренней и внешней цепей, что является более частым случаем при испытании оплеток, не входящих в состав кабеля со стандартным волновым сопротивлением, проделывая указанные выше аналогичные преобразования, получаем следующее выражение для сопротивления связи:

Т к (

Z _св = 4 Z_{В    T}

V ₀

η ( ω )

где

η ( ω ) =^⎪⎨

× ( 1

^к Z_В

ZВ

- 2

-

кк ε ^{к ZВ} + 1 ^{⎞⎛ ZВ} + из ТТ Z В   ⎠⎝ Z В

× sin ω

⎟×

ε к _× из

μ 0 ε 0 ε ^киз L ) ⎪_⎭

⎬ . (37)

Таким образом, в зависимости от качества согласования внутренней и внешней цепи для расчета сопротивления связи можно использовать либо формулу (35), либо формулу (36).

Для исследования экранирующих свойств оплеток коаксиального кабеля использовалась малая триаксиальная линия (МТЛ), внешний вид которой изображен на рис. 2.

Рис. 2. Общий вид конструкции МТЛ в сборе

Работа МТЛ организована следующим образом. К верхнему наконечнику, связанному с внешней цепью триаксиальной линией, подключается генератор сигнала синусоидальной формы для создания электромагнитного поля помех на испытуемом кабеле. Нижний наконечник, связанный с внутренней цепью, соединяется с входом анализатора спектра для снятия амплитуды напряжения наведенного помехонесущего поля. Процесс измерений автоматизирован и управляется с помощью программного комплекса, установленного на компьютере оператора. Графики зависимости сопротивления связи сплошного медного экрана и оплетки ПМЛ-6x10-УЗ от частоты сигнала приведены на рис. 3.

Из сравнения графиков рис. 3 видно, что для сплошного медного экрана сопротивление связи на порядок ниже, чем для оплетки ПМЛ, как и должно быть, поскольку экранирующие свойства кабельного экрана тем выше, чем ниже сопротивление связи. На графиках сопротивление связи растет, что говорит о снижении экранирующих свойств материалов с ростом частоты.