Исследование спектра рассеяния света использованием дельта-функций

Свет представляет собой спектр электромагнитной волны, который позволяет изучать свойства электромагнитных волн в другом диапазоне путем регулирования законов света. Необходимо работать с такими понятиями, как интенсивность света, интенсивность света, яркость, яркость, световой поток, чтобы характеризовать свет в диапазоне видимости. Концепция светового потока - единица измерения люмена, то есть предполагается, что световой поток представляет собой лишь небольшое количество, по сути это энергия, которая падает на поверхность блока со временем. Если мы вычисляем электромагнитные волны, в том числе световой поток, идущий от источника во всех направлениях или распространяющийся в определенном направлении, то мы должны работать с пространственным углом.

Световой поток, падающий под единичным пространственным углом, называется силой света и обозначается как I.

АФ r1Lmi   ТРИ   Wr²   1J * 1т² 1J

] = 1 kd

I П ; [1Sr\ [tn tAs 1s * 1т² 1S

Существует также измерение, называемое освещением, которое характеризуется потоком света в произвольной форме и измеряется в люксах [1-2] .

АФ   1Lm

^E ~H; [1m² = 1 ^LX ]

Подходящий размер для источника света - яркость. Эта величина, которая отражается потоком света во всех направлениях от поверхности источника до поверхности Солнца, называется светимостью. Поскольку P = ∆F / ∆S идентична выражению, это также измеряется в [Lx]. Связь между силой поверхности, величиной поверхности и углом поверхности с потоком света на поверхности может быть четко выражена.

I        I

B = s = s^ [nit]

Освещенность источника света на некотором расстоянии зависит от интенсивности света источника и косинуса угла между источником света и нормальной поверхностью поверхности. Если несколько источников расположены на одной линии и на одном и том же интервале, необходимо учитывать интенсивность и расположение всех источников света на расстоянии. Для теоретического расчета освещения, которое должно быть получено в точках, где устройство должно быть спроектировано и проверено.

^E 1 =^ ^cos(^)                           (1)

где cos( φ ) - косинус угла между энергетической осью и нормальной плоскостью точек, но cos(ph) = 0, поскольку поток в первую точку крутой.

Вторая точка: E_1 = I/(r2 + ∆l_1)2) cos(φ_1). Здесь Δl_1 - расстояние между первым и вторым источником одинаковой интенсивности подряд. cos(φ_1)- угол косинуса между нормальностью точек исследования и потоком из второго источника. Для этого мы сосредоточимся на следующем.

^ 2 - ТГ ^ + А² ; Г 3 - 74 2+2^ 2 ; Г 4 - ТГ Г + За²             (2)

как показано теоремой Пифагора

Гг - 7Г? + (n - 1W                       (3)

У нас есть возможность рассчитать расстояние n, необходимое для расчета освещенности первой точки света от n источников, но если мы хотим рассчитать это выражение с помощью программного обеспечения, оно действительно только для первой точки. Для второй точки необходимо рассчитать влияние первого источника на температуру плавления, предполагая, что эффекты первого и третьего источников одинаково, и что источники n-k и n+k для n-точки равны. Для этого необходимо рассчитать интенсивность всех источников до точки исследования и вывести угол падающего света из суммы общего освещения для одной и той же точки.

cos⁽^) = з ° ; где r_n = jr f + (n - 1W ; cosGpJ = ।    ^r 0 ;      (4)

^ГП                                 ft+n-l)^

Использование программного обеспечения для облегчения вычислений для системы с несколькими источниками и несколькими точками обеспечивает много удобств (Рисунок 2).

E l

E1 = ,       ¹        *

/Гд +((П-1)0.01)2

El =—------ ⁿ     (r² + (0.01*(n-1))²)

I - ; ?

r

Jr02 + ((n-1)0.01)2 r

^н+аниспЛи2

(5), (6)

Это выражение представляет собой n-освещение для первой изученной

точки. Если мы суммируем свет, исходящий от всех источников, мы можем рассчитать общее освещение одной точки.

E_2um-E 1 *2 + E 1 ++Е П- ₃ + Е П-2 + Е П-1 + Е П           (8)

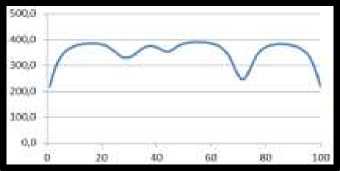
а) 100% активная позиция

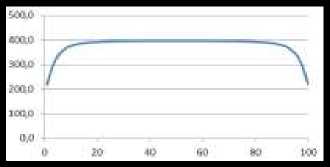
б) 60% активная позиция

Рис. 3 Спектр интенсивности света на определенном расстоянии от источника света.

Ниже мы видим графики, на которых все источники работают, а некоторые из них не работают (рисунок 3). Разложим полученные кривые в якорь дельта-функции, как показано в [3-6].   Мы будем использовать функцию Гаусса (9).

^М = —^^p (~г)    (Ш⁹)

Являются ли коэффициенты x (n _i ) 0 или 1. В этом ш = 0,5 получается.

X(t) = Y^₁H₁x(n_l)^exp(-⁽^^)     (12)(10)

Если значение CH (t) больше или меньше значения в нарисованной линии 0, значение коэффициента равно 1, если оно меньше. Используя этот алгоритм, мы можем показать линию на рисунке 3, используя формулу (10). В то же время роль активных ресурсов определяется коэффициентами равнами 1.

Заключение

Важно выполнить эти расчеты для всех точек и построить график результатов. Если ресурсы являются графическими, когда все они работают, а некоторые из них недоступны, можно будет сообщить источники. В этой работе становится возможным изучать и анализировать события, связанные с добавлением нескольких функций из выводов, сделанных на основе результатов.