Исследование способа формообразования тонкостенных осесимметричных деталей из кольцевой заготовки с применением эластичной среды

Рис. 1. Схема формообразования:

1 – плоский пуансон; 2 – эластичный пуансон;

3 – контейнер; 4 – заготовка; 5 – матрица;

6 – эластичный подпор; 7 – толкатель

J ( ^S дет - ^ST ^{) 2 d} P >  min ,

Ркр где Sдет – заданная толщина детали;

S_T – технологически возможная толщина, которая получается после формообразования заготовки.

Пределы интегрирования обусловлены тем, что утонение заготовки, максимальное, имеет место при p = р к , т.е. когда заготовка прилегла к матрице, так как деформация на матрице блокируется силами трения от действия касательных напряжений между заготовкой и матрицей - т м . Надо иметь ввиду, что наличие цилиндрического технологического участка высотой h с одной стороны при отбортовке уменьшает возможную высоту детали, но с другой позволяет получить более равномерную толщину с большей высо-

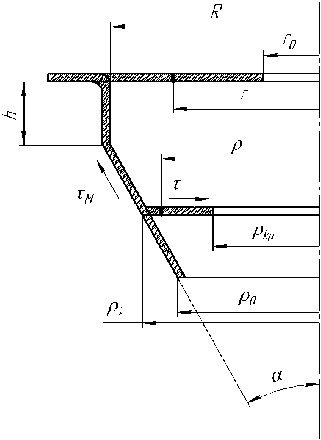
Рис. 2. Геометрическая схема:

ρ _кр – радиус кромки детали; ρ _к – радиус контакта заготовки с матрицей детали; ρ – текущий радиус элементарного участка; r ₀ – радиус отверстия;

h – высота цилиндрического участка;

ρ ₀ – конечный меньший радиус детали

r

ρк   'J

2 R

S дет

R - 1

sin α

RS где R =   , S дет = дет – средняя толщина де-

ρ к          ^S заг

тали.

С учетом (4) тангенциальная деформация ε_θ примет вид:

εθ

= 1 - R ² - ^{S дет} ( R ² - 1 ) , \ sin α

Покажем, что в первом приближении при отбортовке тангенциальная деформации может быть задана при любом законе изменения толщины. Примем в первом случае толщину постоянной для детали, исходя из возможного максимального утонения кромки. На кромке выполняется условие [6]:

εS = -0,5εθ.

той детали. Найдем минимальное значение h , при котором высота конической детали в случае

Приняв на кромке схему напряженного состояния линейной, будем считать ε_θ ≈ δ_ρ ≤ 0,36 (для большинства металлов):

S кр / S заг = 1 - 0,5 ε θ = 0,82 . (6)

утонения равномерного и равного толщине утонения кромки, равно высоте конической детали при традиционном процессе отбортовки, когда толщина детали не постоянна. Анализ показывает, что толщина полученной детали после отбортовки меняется по закону близкому к линейному. Запишем уравнение связи для трансверсальноизотропного тела [4, 5]:

Во втором случае зададимся линейным законом изме н ения толщины при отбортовке:

S + S

S дет ₌ кр заг ₌ 0 91 _{.          (7)}

^Sзаг       ^{2 S}заг       ^,

С учетом формулы (4) угол конусности

детали не должен превышать:

ε _S

• 1    σ_ρ / σ_θ + 1 ^ε θ ^,

• 2    µσρ/σθ-1

sin α = S дет

- 1

2 R

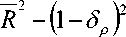
где µ – коэффициент анизотропии трансверсально-изотропного тела;

• σ ρ – напряжения в меридиональном направлении;

• σ_θ – напряжения в тангенциальном направлении;

• e _θ – деформация в тангенциальном направлении.

Определим величину тангенциальной деформации элементов в момент касания с матрицей

Подставим значения (6, 7) в уравнение (8) и получим при изменении толщины по линейному закону α ≈ 25,5⁰ , при постоянной толщине

₀       RR     r

α ≈ 23⁰ , при этом =    = 1,2 ; ^кр = 1,49 ;

^{ρ r кр          r 0}

ρ =ρ при радиусе кр :

ε _θ = ln ρ / ρ _к ≈ 1 - r / ρ _к .       (2)

^R = 1,79 ; δ _р = 0,36 .

r ₀

Определим соотношение напряжений. Выделим элемент в зоне отбортовки и расставим силы на бесконечно малом элементе на ось « ^î ρ » с известными допущениями (см. рис. 4).

Установим связь между ρ _к и r из условия постоянства объема для конической детали при h = 0 :

( σ_ρ + d σ_ρ )( f ₁ + df ₁) - σ_ρ f ₁ - 2 σ_θ f ₂sin

d θ

- τ ⋅ f 3 = 0 ,(9)

S заг π ( R ² - r ² ) = 2 π

-

2 sin α

к _S

. (3) дет

Из (3) имеем:

где σ_θ – напряжения в тангенциальном направлении;

τ – касательные напряжения между заготовкой и эластичной средой.

Площади:

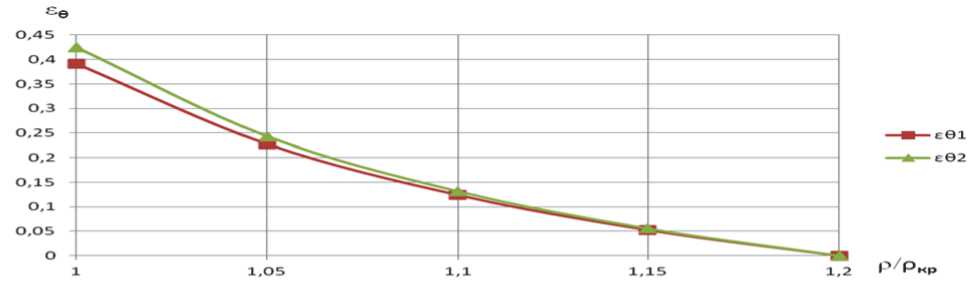
Рис. 3. Изменение деформации заготовки ε_θ для разных законов изменения толщины заготовки. Погрешность в деформациях ε_{θ 1} и ε_{θ 2} составляет не более 8%.

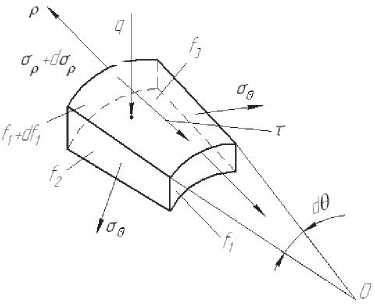
Рис. 4. Схема действия сил

σ = σ (1 - ^кр ) + ^к (1 - ^кр ) . (14) ρ max      S

ρ _к    2 S_Т      ρ _к ²

На рис. 5 представлен график толщи ны, рассчитанной с учетом формулы (1),

S Т - S заг

ε _S =            :

^SТ = 1 +

Sзаг

σ ρ ₊ 1

σ θ    _{⋅ ε}

µ^{σ ρ} - 1   ^θ

σθ

.

f ₁ = ρ ⋅ d θ ⋅ S_{T ,} df ₁ = d ρ ⋅ d θ ⋅ S_{T ,} f ₂ = d ρ ⋅ S_{T ,} f ₃ = ρ ⋅ d θ ⋅ d ρ τ = f ⋅ q ,       (10)

, где f – коэффициент трения;

q – давление.

Подставим (10) в (9):

σ _ρ d ρ + d θ ⋅ S_T + d σ _ρ ⋅ ρ ⋅ d θ ⋅ S_T -

τ ⋅ ρ ⋅ d θ ⋅ d ρ

- σ dθ ⋅ S ⋅ dρ-=

ST dσρ+σρ-σθ-τ =0.(11)

d ρ  ρ ρ S_T

Для решения (11) примем условие пластичности [6]:

σθ =σS ,(12)

Здесь соотношение σ_ρ / σ_θ найдем без учета упрочнения и изменения толщины. Для этого установим связь между соотношениями ρ _кр / ρ _к . Из условия постоянства объема для верхней части

заготовки:

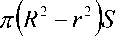
π ( R ²

-

ρ _к ²

sin α

дет ^,

отсюда получим:

_{2    2} ( R - ρ _к )

r = R -          S дет .(17)

sin α

Для нижней части заготовки имеем:

Sзагπ(r2-r02)=Sдетπ(ρк2-ρк2р).(18)

Находим:

r = r0 + (ρк - ρкр )S дет .(19)

где σ _S – предел текучести.

В результате решения уравнений (11) и (12) получим:

Приравняв правые части (15) и (17), выразим:

ρ кр

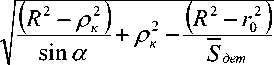
. (20)

τρ σ_ρ = σ _S +   - σ

ρ S  2 _{S Т}

τρ ²

_S           кр или

ρ  2 S_Т ρ

ρ кр

-

При построении графика толщины соблюдаем следующую последовательность расчета. Задаем-

ρ    τρ   ρ

σ_ρ = σ _S (1 - ^кр ) +      (1 - ^кр ) . (13)

ρ   2 S_Т    ρ

Напряжения в зоне контакта определим при ρ = ρ _к :

ся исходными данными: R , sin α , S дет =

r ₀

_         ρ ₀

По формуле (16) при r = r ₀ , ρ _к = ρ ₀ определяем:

_r 2   ( R ² - ρ ₀ ² )

r ₀ = R -            S дет .     (21)

sin α

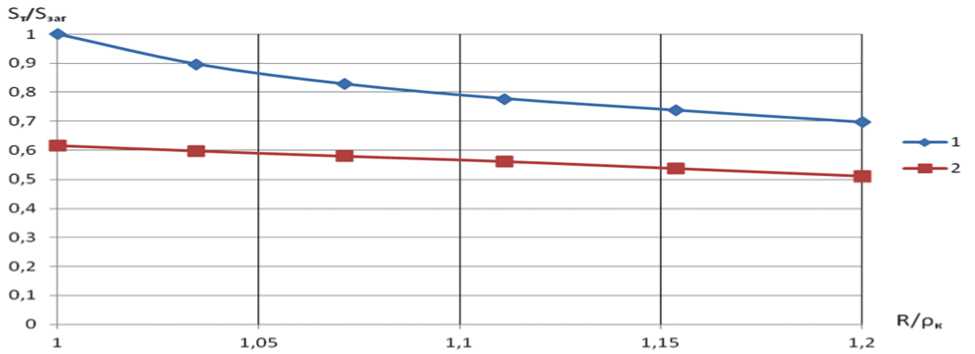
Рис. 5. График изменения толщины конической части детали при отбортовке при R = 30 мм; а = 20°; Sdem = 0,3мм; as = 5 кг/мм2; ц = 0,5; h = 1,5мм; t = 0,008;

1– без цилиндрического участка; 2 – с цилиндрическим участком

Далее по формуле (20) рассчитывается: р кр , где r d ^ Р к ^ ^R •

При заданном т = f • q , находим I_p max по формуле (14).

По формуле (5,15) определяем £ 9 и S_T I S заг •

Рассмотрим случай отбортовки с цилиндрическим участком на большем диаметре. По аналогии с предыдущим анализом получим:

R 2 — S dem -----(R 2 — р2 )- 2hRS dem sin а

' 9 = ¹--

Р к

,(22)

.      -            R ² — 1

sin а = Sdem —--- ---- ----- ;-----Г- , (23)

R — 2 hRS dem — ( 1 — 5 _р ) 2

закону близкому к линейному. Представим:

Sb- = 1 +

Sзаг

+ 1

I---8 9 = ф о + Ф 1 h •    (28)

CTp — 2

^ 9

Правая часть записи - это разложение функции в ряд, где

! IP + 1

ф _о = 1 + =----- 8₉ при h = 0 ; S dem = 1 •

Ip — 2

!p +1

ф ₁ = =^---- 8₉ при h = 0,

Ip — 2

^£ 9

R

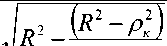
при h = 0 ; S dem = 1 .

r o =

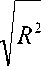
— 2 h • R • S dem

R ² — Р 0² c

S дет ^, sin а

В выражении (28) соотношение напряжений примем постоянным, не зависимым от h .

Условие минимизации (27) примет вид:

dem — ф ₀ — ф ₁ h ] d p _K ^ min .    (29)

p 0

Если цилиндрический поясок h считать технологическим припуском, то его величину определяем путем использования условия минимизации (1) по высоте цилиндрического пояска. Высота h обеспечивает получение детали с минимальной разнотолщинностью, близкой к постоянному значению.

Взяв производную по h и заменив интеграл конечной суммой, получим:

R

J

P o

S дет

^^^^^^^B

1+

V

I 1 I + 1

I I I — 2

A12

8 у

d p _K ^ min .(27)

В выражении (27) составляющее в круглых скобках представляет технологически возможную толщину при отбортовке, которая меняется по

nn

^(S demф1 )—£ф0Ф1 )

h = ^=--------•     (30)

±(ф=)

i = 1

На рис. 5 представлен график изменения толщины детали с цилиндрическим пояском h = 1,5 мм , наличие которого приводит к снижению разнотолщинности детали. Для приведенных построений (см. рис. 5) высота h рассчитана в первом приближении. В нулевом приближении толщина детали равна толщине заготовки. Пред-

ложенная схема формообразования позволяет получить детали с меньшей разнотолщиностью при большем утонении.