Исследование способности высокопрочной стали к пластической деформации при изгибе на угол 90°

Цель данной работы - определение минимального отношения R/h для высокопрочной стали твердостью 400 HBW (табл. 1) при изгибе на угол 90° методом свободной гибки [5]. В работе принимали участие ООО «Термодеформ-МГТУ» [6] и ЦКП НИИ Наносталей [7].

Методика проведения исследований

Определение минимального отношения R/h для исследуемой высокопрочной стали твердо -стью 400 HBW проводили на основе математического моделирования в программном комплексе Deform-3D.

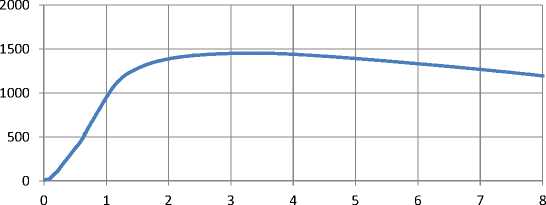
Первоначально для получения данных о пластических свойствах исследуемой высокопрочной стали (кривой упрочнения) (рис. 1) были проведены испытания на растяжения в соответствии с ГОСТ 1497-84.

По полученным экспериментальным данным (рис. 1) в программном комплексе Deform3D был задан новый материал и на основании полученной зависимости проведено конечноэлементное моделирование процесса растяжения с целью определения критерия разрушения ( К ) для исследуемой высокопрочной стали. В качестве критерия разрушения при этом был принят нормализованный критерий Кокрафта-Латама [8-10].

Результаты исследований

По результатам математического моделирования нормализованный критерий разрушения К для данной стали равен 0,65 (рис. 2).

В расчетах изгибающий инструмент представлен в виде абсолютно твердого тела. Кинематическая модель изображена на рис. 3.

Таблица 1. Характеристики исследуемой высокопрочной стали

Механические свойства
HBW	0 о,2 , Н/мм2	ов, Н/мм2	А 5 , %	KCV-20, Дж/см2
не менее или в пределах
370-430	1000	1250	10	50

£, %

Рис. 1. Кривая упрочнения для исследуемой высокопрочной стали твердостью 400 HBW, полученная при испытании на растяжение

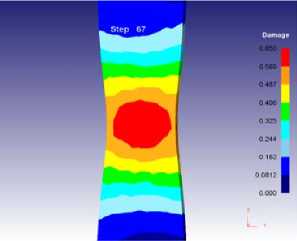
Рис. 2. Конечно-элементная модель разрушения образца исследуемой высокопрочной стали при моделировании в программном комплексе Deform-3D

Рис. 3. Кинематическая модель процесса свободной гибки исследуемой высокопрочной стали в программном комплексе Deform-3D

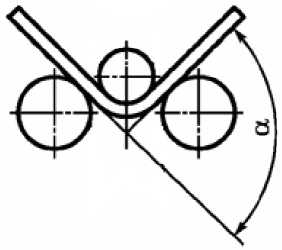
Рис. 4. Угол изгиба α при свободной гибке

Расстояние между опорами V рассчитывалось по формуле

V = Dn + 2h + -, п 2, где Dп – диаметр пуансона.

В процессе свободной гибки в стали помимо пластических деформаций присутствуют также упругие деформации [1]. В результате после снятия нагрузки заданный угол изгиба уменьшается на величину угла пружинения. Величина этого угла зависит от механических свойств и толщины материала, радиуса гибки, а также формы детали. Для компенсации угла пружинения при гибке вводится поправка, т.е. деформация заготовки осуществляется на угол, больший необходимого. В расчетах минимально необходимый угол изгиба α (рис. 4) был принят равным 120º для компенсации максимально возможного угла пружинения при изготовлении деталей с углом изгиба 90° из исследуемой высокопрочной стали.

Определение минимального отношения R/h для исследуемой высокопрочной стали осуществлялось путем варьирования радиуса пуансона R по отношению к толщине изгибаемого металла h до тех пор, пока фактический угол изгиба не достигал минимально необходимого значения без превышения критерия K .

В процессе моделирования гибки исследуемой высокопрочной стали толщиной 8 мм при R/h = 2,5 максимальный угол изгиба до момента превышения критерия К составил 72º (рис. 5).

Для увеличения угла изгиба отношение R/h было увеличено до 3,0. При таком отношении максимальный угол изгиба равнялся 123º (рис. 6).

Для подтверждения результатов, полученных при математическом моделировании, были проведены реальные испытания свободной гибки исследуемой высокопрочной стали. Гибке подвергался образец размерами 8х15х250 мм, отношение R/h в соответствии с результатами математического моделирования было принято равным 3,0. Ширина ручья была рассчитана в соответствии с формулой (1) и равнялась 72 мм. По результатам реальных испытаний трещина по боковой поверхности изгибаемого образца образовалась при угле изгиба 128° (максимальный угол по результатам математического моделирования 123º) (рис. 7).

Полученные результаты реальных испытаний доказали адекватность данных, полученных по результатам математического моделирования, поскольку расхождение между ними составило 5 %.

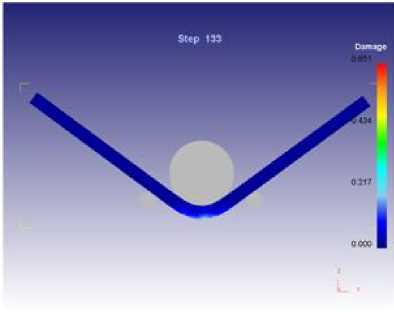
Рис. 5. Распределение значений критерия разрушения для стали толщиной 8 мм при

R/h = 2,5

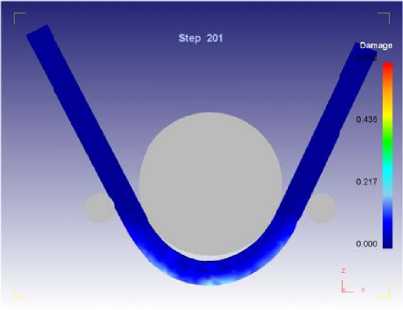
Рис. 6. Распределение значений критерия разрушения для стали толщиной 8 мм при

R/h = 3,0

Рис. 7. Трещины, полученные в результате реальных испытаний исследуемой высокопрочной стали на изгиб

Таблица 2. Минимальное отношение — для получения деталей с углом изгиба 90° п

h, мм	^ п
	направление прокатки
	поперек	вдоль
≤7	2,5	3,0
8-14	3,0	4,0
15-19	3,0	4,0
20-80	4,0	5,0

Аналогичным образом путем варьирования радиуса пуансона R по отношению к толщине изгибаемого металла h были подобраны минимальные значения данного отношения для исследуемой высокопрочной стали толщиной 6-80 мм (табл. 2).

Выводы

• 1.    С использованием программного комплекса Deform-3D создана кинематическая модель процесса свободной гибки.

• 2.    Для проверки адекватности данных, полученных с использованием созданной кинематической модели, проведены реальные испытания исследуемой высокопрочной стали твердостью 400 HBW на изгиб.

• 3.    С использованием конечно-элементной математической модели в программном комплексе Deform-3D проведено моделирование процесса свободной гибки и определены минимальные отношения радиуса пуансона к толщине изгибаемого металла ( R/h ), обеспечивающие получение деталей с углом изгиба 90° из исследуемой высокопрочной стали толщиной 6-80 мм.

Работа проведена при финансовой поддержке Минобрнауки России в рамках реализации комплексного проекта по созданию высокотехнологичного производства, выполняемого с участием российского высшего учебного заведения (договор 02.G25.31.0105).