Исследование стационарных решений задачи динамики фитопланктона с учетом трансформации соединений фосфора, азота и кремния

1,2,3,4 Don State Technical University, Rostov-on-Don, Russian Federation

Образец для цитирования. Белова, Ю. В. Исследование стационарных решений задачи динамики фитопланктона с учетом трансформации соединений фосфора, азота и кремния / Ю. В. Белова [и др.] // Вестник Донского гос. техн. ун-та. — 2019. — Т.19, №1. — С. 4–12.

Введение. В связи с развитием крупных городов на побережье мелководных водоемов и речных систем, впадающих в данные водоемы, участились случаи эвтрофикации. Рост водорослей в водоемах вызван увеличением стока азотных и фосфорных соединений с прилегающих районов суши. Каждый водный объект является уникальным и требует подробного исследования. Для изучения водоемов прибегают к натурным исследованиям [1], а также математическому моделированию. Не преуменьшая роли натурных экспериментов можно сказать, что математическое моделирование является менее затратным, а также позволяет прогнозировать поведение экосистемы.

Для изучения Азовского моря разработана трехмерная модель гидродинамики [2, 3], включающая уравнения движения по трем пространственным направлениям. В работе [4] данная модель выполнена для случая динамического перестроения геометрии расчетной области за счет приливно-отливных явлений. Исследование точности данной модели приведено в работе [5]. В работах [6–8] приведена реконструкция экологической катастрофы, произошедшей в 2001 году, вызванной чрезмерной концентрацией водорослей в восточной части Азовского моря. В работе [9] предложены методы борьбы с заморными явлениями, возникающими в Азовском море. Работы [10–12] посвящены изучению динамики фито- и зоопланктона.

Состояние вод в мелководных водоемах быстро меняется и математические модели требуют уточнения. Расчет параметров трехмерной модели динамики фито- и зоопланктона является трудоемким, поэтому предлагается для расчета данных параметров использовать упрощенную модель.

Цель данной работы состоит в уточнении параметров модели динамики фитопланктона с учетом трансформации соединений фосфора, азота и кремния, при которых наступают стационарные режимы в предположении пространственно- однородного распределения субстанций.

Материалы и методы. Модель основана на системе уравнений транспорта биогенных веществ [15, 16], вид которой для каждого модельного блока F i имеет вид

Механика

— + u — + v — + w — = div (k grad q ) + R , dt     dx     dy      dz                i’    qi где qi — концентрация i-ой компоненты, [мг/л]; ieM, M= {F1, F2, F3, PO4, POP, DOP, NO3, NO2, NH4, Si};

{ u , v , w } — компоненты вектора скорости водного потока, [м/с]; к - коэффициент турбулентного обмена, [м²/с]; R_q — функция-источник биогенных веществ, [мг/л∙с].

В уравнении (1) индекс i указывает на вид субстанции (таблица 1).

Таблица 1 Биогенные вещества в модели динамики фитопланктона

Номер	Обозначение	Название
1	F 1	зеленая водоросль Chlorella vulgaris
2	F 2	синезеленая водоросль Aphanizomenon flos-aquae
3	F 3	диатомовая водоросль Sceletonema costatum
4	PO 4	фосфаты
5	POP	взвешенный органический фосфор
6	DOP	растворенный органический фосфор
7	NO 3	нитраты
8	NO 2	нитриты
9	NH 4	аммоний
10	Si	растворенный неорганический кремний (кремниевые кислоты)

Химико-биологические реакции описаны следующими уравнениями

R F ^- C (1 ^— K_F R ) q_F_ ^— K_Fpq_F, ^— K^q , i ^- 1,3,

R DOP

— 2 sPKFEqF + KPDqPOP i-1

^^^^^™

K DN q DOP ,

R PO 4

- 2

i - 1

S p C f ( K fr

1 ) q F ⁺ K PN q POP ⁺ K DN q DOP ,

R NH 4

- 2 S n C f, ( K fr

—

^f N ^{1 (} q NH 4 )              3

¹) —, -----------? q_F + 2 sN ( ^kfd

/n ⁽ q NO 3 ^,q NO 2 ^,q NH 4 )        i ^{- 1}

⁺ K F-E ) q F   ^K 42 q NH 4 ,

^R NO 2 ^- 2 s N C F i . ^{( K} F i R i - 1

1) ^f N ( q NO 3 ,q NO 2 , q NH 4 ) ^f N ⁽ q NO з ,q NO 2 ,q NH 4 )

■             qF, + K42 qNH4   K23 qNO2, qNO2 + qNO3

_ 3                      ^{f NN )(} q ^NO 3 ,q ^NO 2, q ^NH 4 )       ^q NO3            _

^R NO₃   ² s N ^CF, ⁽ K_F, R   1 )    /                \                q_F, ⁺ K 23 q NO ₂ ,

^1-1                     f N ⁽ q NO ₃ ^,q NO ₂ ^,q NH ₄ ) q NO 2 ⁺ q NO ,

^R Si ^- s Si ^C F ₃ ^{( K} F,R - 1 ) q F, ⁺ s Si ^K F,D q F₃ ^.

Здесь KFR — удельная скорость дыхания фитопланктона; KFD — удельная скорость отмирания фитопланктона; KFE — удельная скорость экскреции фитопланктона; KPD — удельная скорость автолиза РОР; KPN — коэффициент фосфатофикации РОР; KDN — коэффициент фосфатофикации DОР; K42 — удельная скорость окисления аммония до нитритов в процессе нитрификации; K23 — удельная скорость окисления нитритов до нитратов в процессе нитрификации, sP , sN , sSi — нормировочные коэффициенты между содержанием N, P, Si в органическом веществе.

Скорость роста фитопланктона определяется выражениями:

^CF _]2 = ^KNF 1, ₂ min { Jp ^{( q}PO ₄ ) , Jm ⁽ q NO ₃ ^,qNO, ^,qNH ₄ ) } ,

^Cf₃ = K F min { f P ( q PO ₄ ) , f_N ( q No, ,q NO 2 ,q NH 4 ) , Z sA q » -) } , где K NF — максимальная удельная скорость роста фитопланктона.

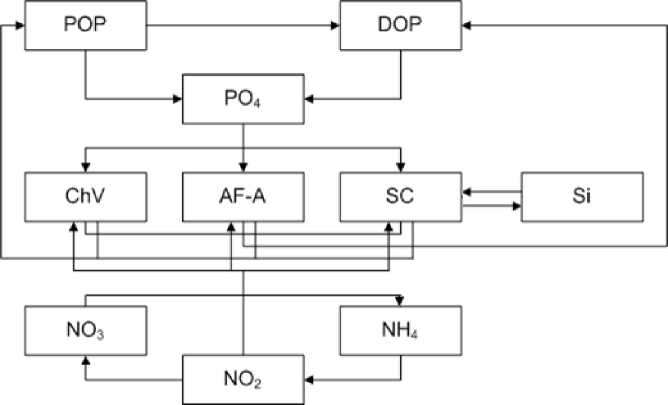
Рис. 1. Модельная схема биогеохимической трансформации форм фосфора, азота и кремния

Функции, описывающие содержания биогенов

• ^-    для фосфора f ( q_P o ) =--- q PO 4   ,

q po 4 + K po 4

где K_PO — константа полунасыщения фосфатами;

• ^-    для кремния f ( q_Si ) =--- Si— , q_s . + K_s .

где K_Si — константа полунасыщения кремнием;

• ^-    для азота f_N ( q_NO 3 , q_NO 2 , q_N H 4 ) = f N ¹’ ( q O , q_NO 2 , q_N H 4 ) -Г ( q H 4 ) ,

• ^{3     2     4}          K NO 3 ^{+ (} q NO 3 + q NO 2 )                  ⁴     K NH 4 ⁺ q NH 4

где KNO — константа полунасыщения нитратами, KNH — константа полунасыщения аммонием, Kpsi — коэффициент ингибирования аммония.

Для системы (1) необходимо задать векторное поле скоростей водного потока, а также начальные значения функций концентраций q_i

• q ( X , y , z ,0 ) = q i ( x , y , z ) , ( x , y , z ) e G ., t = 0, i e M . (2)

Будем считать, что граница 2 цилиндрической области G является кусочно-гладкой и S = SH и2o ист, где 2H — поверхность дна водоема, 2o — невозмущенная поверхность водной среды, ст — боковая (цилиндрическая) поверхность. Пусть ип — нормальная по отношению к 2 составляющая вектора скорости водного потока, n — вектор внешней нормали к 2 . Для концентраций qi будем пред- полагать:

– на боковой границе:

q i = 0, на ст , если u_n <  0 , i e M ;                                         (3)

d q

Механика

—'- = 0, на ст , если u >  0, i e M ;                                      (4)

n dn

• -    на 2 _o — поверхность водоема:

^ qi- = 0, i e M ; 5 z

• -    на дне 2 _H :

k^q- = е^, ie{Fb F2, F3}, dz k^q- = e2 q, zg{PO4, POP, DOP, NO3, NO2, NH4, Si},                         (6)

d z    ²

где e_{1 ;} , e₂ , — скорости осаждения водорослей и питательных веществ на дно.

Стационарный режим . Рассмотрим случай пространственно -равномерного распределения субстанций (фитопланктона, форм фосфора, азота и кремния), тогда каждое из уравнений (1) упрощается и в результате получаем следующую систему обыкновенных дифференциальных уравнений (ОДУ):

dq _F

—~ = Ср (1 — Kp r ) qp — KpDqp — Kppqp , , = 1,3, (7)

F      FR F     FD F     FE F dt dqPOP dt

^dq DOP dt

^Z s P K FD q F, - ^K PD q PCP - ^K PN q PCP , i = 1

^Z S p K FE q F + ^K pD q pc>P ^{— K} DN q DOP , = 1

^d q pc 4 dt

3                ,

= Z S p C f ( K fr i = 1

q F + ^KPN q PCP + ^KDN q DCP ,

^dq NH 4 dt

3                            f .⁽²⁾ ( NH. )              3

= Z S N C F ( ^K FR ^{- 1 )} f N ( NO ₃, no ₂ , NH 4) ^q F ^{+ Z s} N ^{( K} F^D + K FE ) ^q F ^{— K 42} q ^NH 4

dq NO 2 dt

Z S n c f ( K fr i = 1

—

₁₎ f ® ( NC 3 , NC 2 , NH J     q Nc 2

f N ( NC 3 , NC 2 , NH J q _N c 2 + qN/ F

^{+ K} 42 q NH ₄   ^K 23 q NC ₂ ’

dq pc , dt

= Z s_NC_F ( K_M — 1 ) i = 1

f<')( NC3, NC2, NH)    qNc, fN (NC3,NC2,NH4) q„c2 + qNc3

q F ^{+ K} 23 q NC ₂ ,

qS^- = s,.C K_F „— 1 q_F + s_FK_FFq_F . dt       ^{S F} 3     ^F 3 R        ^F 3      ^{S F} 3 ^{D F} 3

Решим систему обыкновенных дифференциальных уравнений методом Рунге -Кутты [15-17]. Проведем несколько численных экспериментов, предполагая, что развитие фитопланктона зависит от единственного лимитирующего вещества.

Результаты исследования. Для системы ОДУ (7) рассчитаем начальные условия и параметры уравнений, при которых наступают стационарные режимы. Возьмем начальные значения концентраций: q _F ( 0 ) = 2,5 мг/л , q F ( 0 ) = 2,6 мг/л , q _F^ ( 0 ) = 0,91 мг/л , q _PCP ( 0 ) = 0,07 мг/л , q _DCP ( 0 ) = 0,07 мг/л , q _{PC i} ( 0 ) = 0,005 мг/л , q _NHi ( 0 ) = 0,11 мг/л , q _NCi ( 0 ) = 0,0178 мг/л , q _NC ( 0 ) = 0,304 мг/л , q _Si ( 0 ) = 0,4 мг/л ; коэффициенты: K_NF = 2,8 сут^- , K_FR = 0,15 сут^- , K FD = 0,05 сут^- , K FE = 0,15 сут^- , K_PD = 0,015 сут^- , K_PN = 0,02 сут^- , K dn = 0,1 сут^- , K 42 = 0,9 сут^- , K 23 = 2,5 сут^- , K p _S , = 1,46 сут^- , S p = 0,01, S n = 0,016, s s, = 0,023, K_PCj = 0,024, K pc 3 = 3,0, K nh ₄ = 2,0, K_Si = 3,0.

Полученные стационарные режимы системы ОДУ (7) в предположении, что развитие фитопланктона лимитируется единственным биогенным веществом —фосфором, азотом или кремнием — изображены на рис. 2-4 соответственно. Рис. 2 описывает влияние фосфора на развитие различных видов фитопланктона, рис. 3 описывает влияние азота на развитие различных видов фитопланктона, рис. 4 описывает влияние азота на развитие диатомовых водорослей.

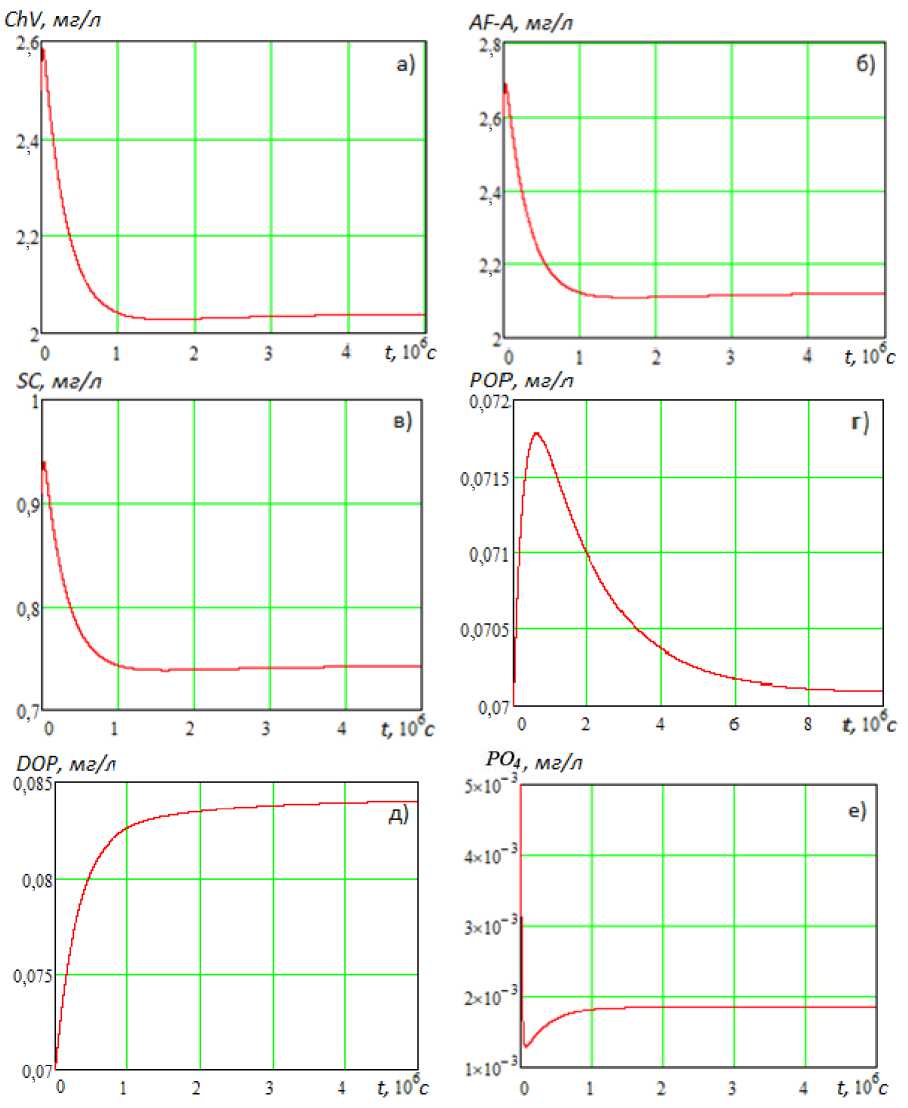
Рис. 2. Стационарный режим системы ОДУ в предположении, что развитие фитопланктона лимитируется фосфором: а) зеленая водоросль ( ChV ), б) синезеленая водоросль ( AF-A ), в) диатомовая водоросль ( SC ), г) взвешенный органический фосфор ( POP ), д) растворенный органический фосфор ( DOP ), е) фосфаты ( PO 4 )

В результате вычислительного эксперимента видно, что при указанных выше значениях начальных концентраций и параметров уравнений наступают стационарные режимы для системы ОДУ (7), описывающей случай пространственно-равномерного распределения субстанций. Полученные значения в дальнейшем будут использованы для моделирования пространственно-неоднородного распределения субстанций, солености и температуры с учетом движения водной среды [18].

Механика

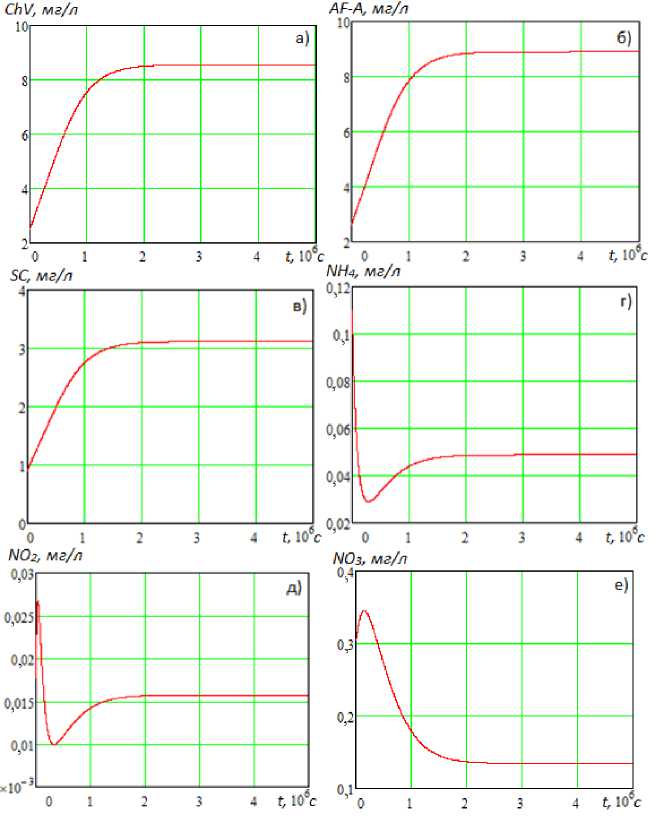
Рис. 3. Стационарный режим системы ОДУ в предположении, что развитие фитопланктона лимитируется азотом: а) зеленая водоросль ( ChV ), б) синезеленая водоросль ( AF-A ), в) диатомовая водоросль ( SC ), г) аммоний ( NH 4 ), д) нитриты ( NO 2 ), е) нитраты ( NO 3 )

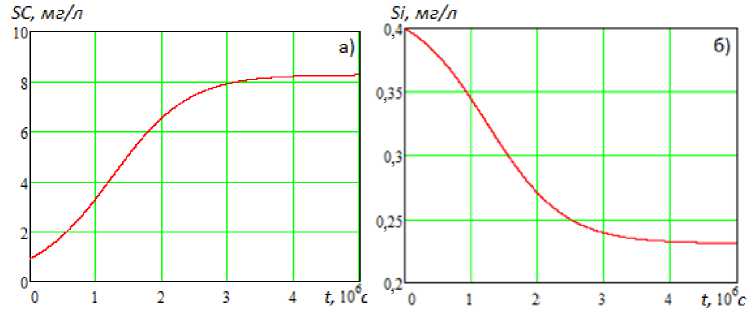
Рис. 4. Стационарный режим системы ОДУ в предположении, что развитие фитопланктона (диатомовых водорослей) лимитируется кремнием: а) диатомовая водоросль ( SC) , б) кремний ( Si )

Заключение. В данной работе исследована математическая модель трансформации форм фосфора, азота и кремния в задаче динамики фитопланктона. Рассмотрен случай пространственно-равномерного распределения субстанций (фитопланктона, форм фосфора, азота и кремния). Система разбивается на три системы обыкновенных дифференциальных уравнений, каждая из которых моделирует зависимость роста фитопланктона от единственного питательного вещества. Эти системы решены методом Рунге-Кутты, получены стационарные режимы (рис. 2-4), для которых определены значения параметров системы и начальные условия.

Полученные результаты будут использованы для дальнейшего моделирования динамики фитопланктона с учетом трансформации соединений фосфора, азота и кремния с учетом конвекции-диффузии, солености, температуры.

Поступила в редакцию 20.11.2018

Сдана в редакцию 21.11.2018

Запланирована в номер 11.01.2019

Received 20.11 .2018