Исследование статических и динамических режимов процессов массообмена

Для математического описания процессов массо-обмена в ректификационных колоннах широко используются системы уравнений в частных производных [1; 2]. Такое описание вполне естественно для колонн насадочного типа, но требует отдельного обоснования для тарельчатых колонн, так как в последнем случае объект по своей природе дискретен. В [2] был развит подход, основанный на детальном рассмотрении процессов для отдельной тарелки. На основе физических представлений о гидродинамике жидкости в тарелке и барботаже парового потока были получены уравнения баланса массы с учетом фазо- вого перехода компонентов [2]. В результате проведенных исследований построена система обыкновенных дифференциальных уравнений, а затем и в частных производных, с использованием формул разложения Тейлора в предположении малого различия параметров потока на соседних тарелках. Полученная система уравнений в частных производных для тарельчатых колонн имеет такой же вид, что и для насадочных, благодаря чему возможно описание колонн различного типа с помощью единого математического аппарата и сравнительно несложного пересчета параметров для колонн различных типов.

Рассмотрим систему уравнений, описывающую массообмен для бинарной смеси в ректификационной колонне тарельчатого типа [2]:

d t ( ( HS 1 + S 2 h ( H ) ) nx ) -A l ^ Qx * =

• k, nD3/\ ----(y - kx ) + Ф1,

6 т

— (S ₂ ( A l - h ) ny ) + A l — ^[ k ^{т П} D y 1

d t^{v 2V} ’      d i (    6т     J

k _т n D ^{3/ n}

6 т

( kx - y ) ^{+ ф} 2 ,

где x , y - массовые, а п , n - мольные концентрации компонентов в паре и жидкости соответственно; H , h ( H ) - уровень жидкости в переливном патрубке и на тарелке; Q - поток жидкой фазы; A l - расстояние между тарелками; S 1 , S ₂ , k _т , D - геометрические параметры тарелки; т - величина, характеризующая время образования пузырька пара в жидкости; Ф 1 , Ф ₂ - функции внешнего воздействия, обусловленные вводом и выводом потоков сырья и целевых продуктов.

Большой интерес представляет исследование различных нестационарных режимов, в частности процессов установления. При малых отклонениях от равновесного состояния возможно проведение линеаризации системы и использование метода стоячих волн для исследования спектра собственных частот. Несмотря на простоту, этот метод позволяет не только получить качественное представление о характере процесса установления, но и определить важные количественные характеристики времени установления, резонансные свойства системы, а также выявить области неустойчивости в пространстве параметров системы.

Вычисление времени установления необходимо по двум причинам: во-первых, это важно для прогнозирования времени перехода с одного стационарного режима к другому при изменении скорости поступления сырья или его состава; во-вторых, это нужно для оптимального проведения расчетов в более сложных программах решения системы (1) по конечноразностной методике. В этом случае программа вычисления собственных частот и времени установления включается как блок в общую программу и позволяет выбрать оптимальный шаг интегрирования по времени, совместимый с устойчивостью и удовлетворительной аппроксимацией. Для контроля точности расчетов по конечно-разностной методике в качестве тестовых также могут быть использованы аналитические решения, представленные в виде суперпозиции стоячих волн.

Если известно N собственных значений, то можно выписать соответствующее N параметрическое семейство решений в виде uNu

I | = Е Сп I n| eXn, (2) VVJ n=1 V vn / где un, vn - собственные функции частот; Xn - комплексные числа; cn - произвольные коэффициенты.

Для применения конечно-разностной методики к решению системы (1) введем следующие обозначения: u = ( HS 1 + S ₂ h ( H ) ) nx , v = ny , k_y = ^T^ ⁿ . Линеаризуя (1) в окрестности стационарных параметров, получим систему без учета внешнего воздействия:

du . d u       /* \

--A— = D, v - k u , dt      dl’ dv   Ddv/,♦

— + B— = D2 k u - v , dt      dl/’

где A , B - величины, пропорциональные скоростям потоков. Граничные условия с учетом рециркуляции взаимодействующих для этой системы можно записать в виде [2]:

dudv

«1 — + Р1 — = Yi u + 81 v, dtdt l = 0,

dudv a2 , +в2 , = Y 2 u +82v, l = L, dtdt

где a i , P i , y i , 8 i ( i = 1,2 ) - коэффициенты, зависящие от параметров потоков в кубе ( l = 0) и дефлегматоре ( l = L ). Конкретный вид этих коэффициентов приведен в работе [2].

Решение задачи (3), (4) ищем в виде u = u (l) eX t, v = v (l) eX t.

Подставим эти решения в систему (3) и граничные условия (4):

u ( l ) X- Au ' ( l ) = D 1 ( v ( l ) - k * u ( l ) ) ,

v ( l ) X + Bv ' ( l ) = D ₂ ( k * u ( l ) - v ( l ) ) , a 1 X u ( 0 ) + p 1 X v ( 0 ) = Y 1 u ( 0 ) + 8 1 v ( 0 ) , l = 0, a ₂ X u ( 0 ) + в ₂ X v ( 0 ) = y ₂ u ( 0 ) + 8 ₂ v ( 0 ) , l = L .

Решим систему (5):

u (l ) = aeцl, v (l ) = be^.

Подставляя u ( l ) и v ( l ) в (3), получим систему на собственные значения X:

aX- Aa ц = D1 (b - k* a),

bX + ВЬц = D2 (k * a - b), из которой найдем выражения для ц1 2 (X):

• 1    [X X D ₂ D . k * 1

Ц =               1±

• ^1,2 2 1 A B B A J

1 [X  X D ₂   D , k * | X ²    X D ₂   X k*D ,

.

запишем в векторном виде:

у

и I

= а_х v J

—(Х —Ац + Dik )

e ^ц 1 + ^x t

у

⁺ a 2

— ( ^{Х — А ц} 2 ⁺ D i k )

^ц 2 l ^{+x t} e .

Для определения X и, следовательно, ц ( Х ) и ц ₂ ( Х ) воспользуемся граничными условиями (6). Подставляя решение (7) в граничные условия при l = 0 и l = L , получим:

Зная число корней, определим сами корни, воспользовавшись формулой [3]:

¹ Г f ^{( (Х)} Л-v N ^Х^мГ ^{d X} = L n k ^a k ,

2пf(X)    и где ak - корень уравнения f (X) = 0; nk - его кратность.

Согласно этой формуле составим систему

1 г f '(X)

Х,+Х₂ + ... + Х = — Х^-Н) d X,

^{1    2} n 2 п i C f ( X )    ’

X ² +х ² + +х ² = — fx ^{2 Mx l} d X ,

^{1    2} n IUC f ( X )     ’

a-ext Г Ха, — у, + (Хр, — 5])—^Х — Ац + —k j | + I

+a2ex1I Ха, — у, + (Хр, — 5,)—(X — Ац2 + —k*) I = 0, l = 0, I                   /Г')

^a 1 e Ц I ^Ха 2

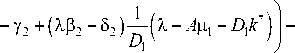
+ a₂e ^{Ц 2 L} I Ха₂ — у₂ + ( ХР₂ — 5₂)—(X — А ц₂ + —k *) I = 0, l = L .

I

Итак, мы имеем систему уравнений для коэффициентов решения (7) a ₁ , a ₂ . Ее определитель должен быть равен нулю:

f ( Х ) = e ^{Ц 2 L} I Ха, — у, + ( ХР, — 5, )—( Х — А ц, + —k *) Iх

I х| Ха2 — у2 +(ХР2 —52)—(X — Ац2 + —1 k*) | =

I                     —1                 )(8)

= — e ^{Ц 1 L} I Ха₂ — у₂ + (ХР₂ — 5₂)—(Х — А ц + —k *) I х

I

X N +x N + ... +x N = — fx ^{Nf (X} ) d X ,

1      2 n 2niC f(X)

которая решается внутри достаточно большого контура C .

При исследовании асимптотики необходимо исходить из конкретных граничных условий. Поэтому возьмем задачу, например из работы [2], и применим к ней конечно-разностную методику.

Граничные условия из работы [2] приведем к виду dv wc

H. — = с, и--v — c2v, l = 0, k dt

Hc du Vc d 2 — = c7v — -S-u u, l = L,

Ld dt где Hk, Hd, c1, c2, Vd, Ld, W - известные коэффициенты, откуда для системы (6) получим:

а1 = 0, Р1 = cTHk-, Y1 = c1, 51 =— c21 W +1 VdV х| Ха1

^{— у} 1 ⁺ ( ^Х Р 1 ^{— 5} 1 )~ ( ^{Х — А ц} 2 ^{+ —} 1 ^k ) D

_ Hdc1  о _ n      _ c1Vd   т _ а2 =    T , e2 = 0, Y 2 = T , 52 = c 2

Ld                 Ld

Вычислив корни Х этого трансцендентного уравнения, мы тем самым найдем спектр исходной задачи, который, вообще говоря, содержит бесконечное число значений Х . Поэтому процесс решения уравнения (8) разобьем на два этапа: сначала определим младшие корни Х внутри достаточно большого замкнутого контура С и получим точное численное решение уравнения (8), а затем исследуем асимптотику при X ^ го .

Для получения точного решения уравнения (8) воспользуемся методами теории функций комплексного переменного. Известно, что число нулей внутри замкнутого контура С аналитической функции f ( Х ) , не имеющей полюсов, определяется по формуле [3]:

N = ' , ' ' d х .

2«iJ f (Х)

В уравнении (8) исключим младшие члены, не содержащие X и первого порядка относительно X, и получим уравнение для достаточно больших X:

e ^⁽ A ⁺ B > ^L

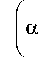
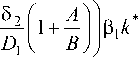
з в1     А а2Х — 1 +—

² — ₁ I    B

.

Числитель правой части, не содержащий X , обозначим с . Тогда

e A ⁽ A ⁺ B > ^L

c

а2Хвх

² — 1

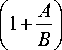
Имея в виду, что X - комплексное число, т. е.

X = ^ + i п , получим:

Х( A + B)L = ln

AB

AB

^ = 7----^ln(A + B) L

c

. P i (, A а₇Х— 1 +—

² D i к B

c

агХ-^^ (1

² D i к

2 п nAB

n = - ------- — + const.

(A + B) L

- In Х ,

AB

——- ln П,

При исследовании полученного спектра { Х n } нужно прежде всего обратить внимание на Re Х n . Если среди комплексных чисел Х n имеются такие, для которых Re Х> 0, то коэффициенты системы таковы, что режим будет расходящимся, и поэтому следует изменить значения параметров.

В заключение рассмотрим величину т = max ।—-—, | Re Х|

–

Перенумеровав полученные Х в порядке возрастания |ReХ|, решение системы (3) запишем в виде суперпозиции стоячих волн:

( г

u

v

= Z e ^Х n t n

+ bn

an

к

— (Хn - AP1 + Di k ) D

А

e ^ ^z

время затухания самой медленной из гармоник, т. е. время установления для всей системы. От этой величины зависит выбор шага интегрирования по времени при расчетах по конечно-разностной методике. При расчетах периодических режимов следует иметь в виду, что существует возможность резонанса при совпадении частоты внешнего воздействия с одной из собственных частот (мнимой частью Х ).

Приведем результаты расчетов, полученные с помощью конечно-разностной методики для прогнозирования поведения решения задачи (3), (4) (рис. 1–4).

Были использованы следующие

— (Хn - AU, + Di k )

e 2 ^z

где a_n , b_n выбираются таким образом, чтобы удовлетворить заданному начальному условию.

₁         u (40, t )

0,8

0,7

0,6

0,5

0,4

0,3

0,2

A = 36 м/с,

B = 360 м/с,

коэффициенты:

D i = D 2 = k y V ,

V ■ A

V = 73,07 кмоль/ч,    к =---- ,

L ■ B

H k = 30 кмоль/ч, W = 76,59 кмоль/ч.

а = 45,21 кмоль/ч,

H d = 50 кмоль/ч,

u (20, t ) 0,9

u (0, t )

3 ′

u (0, t ) 0,1

2 4 6

u (40, t )

u (20, t )

20 22 t , ч

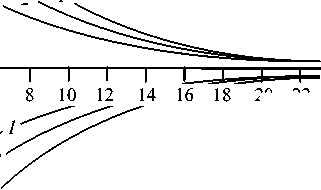
Рис. 1. Кривые переходных процессов при возмущении по концентрации вверху колонны для точек l = 0, 20, 40 м: 1 ′, 2 ′, 3 ′ - при увеличении u ( L ,0 ) на 50 %; 1 , 2 , 3 - при уменьшении u ( L ,0 ) на 50 %

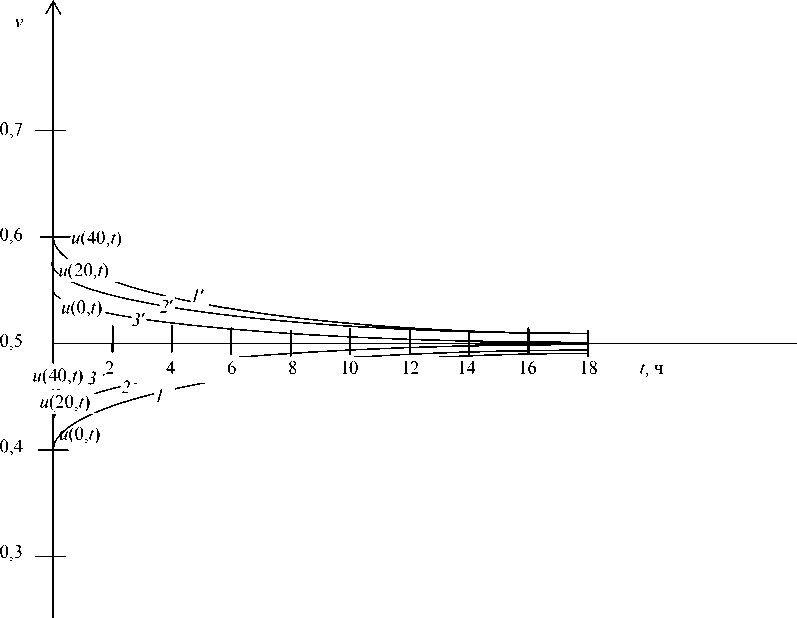
Рис. 2. Кривые переходных процессов при возмущении по концентрации вверху колонны для точек l = 0, 20, 40 м: 1 ‘, 2‘, 3 ‘ - при увеличении v ( L ,0 ) на 50 %; 1 , 2 , 3 - при уменьшении v ( L ,0 ) на 50 %

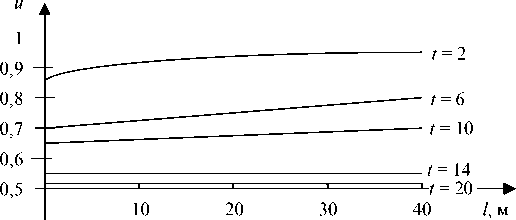
Рис. 3. Профиль концентраций в жидкости по длине колонны при возмущении на 50 % вверху колонны для различных t , ч

v

0,6

0,5

t = 2

t = 6

t = 10

t = 20

0,4

10         20         30         40       l , м

Рис. 4. Профиль концентраций в паре по длине колонны в различные моменты времени при возмущении на 50 % вверху колонны для различных t , ч

Для этих коэффициентов все Re X < 0, что обеспечивает сходимость процесса. Кроме того, можно оп ределить время установления т = max,—-—, = 6,39 ч,

| Re X за которое амплитуда самой медленной гармоники уменьшается в с раз.

В сложных химико-технологических установках, состоящих из ряда соединенных аппаратов и имеющих систему потоков взаимодействия их сред, параметры которых чувствительны к возмущениям, все более важным становится построение высокоэффективных систем контроля и управления. Однако прежде чем создавать такие системы управления, полагая основным ее звеном управляемый объект, необходимо улучшить статические и динамические характеристики этого объекта.

В данной статье предложен подход к решению задачи моделирования нестационарных режимов объектов с рециркуляцией взаимодействующих потоков

(ректификационных установок), основанный на математическом аппарате, содержащем дифференциальные уравнения в частных производных. Для исследования процессов установления применялся метод стоящих волн, который позволяет получить сведения не только о качестве и характере процессов установления, но и определить важные характеристики времени установления, резонансные свойства системы и выявить области неустойчивости в пространстве параметров системы.