Исследование статической устойчивости сложных электрических систем

Широкое внедрение мощных и быстрых цифровых компьютеров в практику диспетчерских и исследовательских расчетов и особенно перспективы их развития [3] устраняют ограничения на использование более трудоемких вычислительно эффективных, но строгих методов анализа устойчивости. Эти обстоятельства создали хорошие предпосылки для применения метода функций Ляпунова в квадратичной форме для анализа малых колебаний сложных ЭЭС.

Расчетный анализ статической устойчивости ЭЭС различной сложности показывает, что наиболее строгим теоретически, удобным для вычислений и эффективным по результатам является использование двух фундаментальных методов - метода функций Ляпунова в квадратичной форме и узловых уравнений [3, 6]. Тем более методы изучения малых колебаний с учетом самораскачивания сложны, поэтому достаточно надежные результаты могут быть получены при строгом математическом описании системы управления для контролируемых объектов с использованием их параметров и характеристик [7, 8].

Методы исследования

Обзор публикаций [3, 4, 6, 9-11] показывает, что применение матричных уравнений Ляпунова и Риккати расширяется, так как роль матричных методов исследования линейных динамических систем возрастает, что связано с разработкой алгоритмов и программ, численных и аналитических методов для их решения. Особое внимание следует уделить интенсивным исследованиям, приводящим к новым и чрезвычайно эффективным методам решения матричных уравнений (в том числе аналитических, основанных на технологии вложения систем - канонизации матриц), широко используемым на практике [9, 11].

Известно [4, 6, 9], что функция Ляпунова в квадратичной форме для линейных дифференциальных уравнений единственная, которая обеспечивает необходимые и достаточные условия устойчивости исследуемой системы при возникновении в ней малых возмущений. Поэтому основой исследований в этой работе является функция Ляпунова в квадратичной форме и узловые уравнения (метод Аллаева), а предметом исследования служат линеаризованные дифференциальные уравнения элементов ЭЭС [3]. Матричные уравнения элементов электрических систем, являющихся основной частью ЭЭС, составлены на основе уравнений переменных состояния, которые получили наибольшее распространение. Рассматриваемые матричные уравнения используются для анализа переходных процессов и статической устойчивости ЭЭС и синтеза оптимальных параметров регуляторов синхронных машин, работающих в сложной электрической системе.

Установившийся режим исследуемой ЭЭС определяется на основе уравнений узловых напряжений. Узловые уравнения, имеющие функциональную связь между токами и напряжениями узлов, наиболее полно описывают электрическое состояние сети любой сложности [10].

В общем случае узловые уравнения можно записать в виде [7, 10]

YU = I + Y_i0U₀ + J * ,

где

y11

Y = — У 1 2

- y 12 - - y in

У 22 ••• — У 2п

.- y ni - y n2 •• •

y n n

матрица проводимости исследовательской системы; I, Yi0, J* - матрицы - столбцы, соответственно, узловых токов, проводимостей связи с балансирующим узлом, источников тока, представляющих собой поперечные ветви с заданными проводимостями.

Для решения узловых уравнений выберем метод Ньютона в полярных координатах, к преимуществам которого можно отнести квадратичную сходимость итерационных процессов, возможность дальнейшего использования для решения задач оптимизации и расчета устойчивости [10]. Кроме того, напряжения узлов U j и углы нагрузки генераторов S j , которые используются в уравнениях Ляпунова, определяемые на основе решения узловых уравнений, содержат всю информацию о состоянии системы, какой бы сложной она ни была [11]. Т Т                                            w                w

На основе вычисленных значений напряжений генераторных узлов и узлов, содержащих вращающиеся машины, последовательно проверяется положительность матриц квадратичных форм Ляпунова, устанавливающих выполнение необходимых и достаточных условий статической устойчивости генераторов (станций) и ЭЭС. По существу, задача анализа статической устойчивости сложной ЭЭС сводится к многократному исследованию схемы «генератор – шины», которая в практических расчетах описывается уравнением порядка не более 4-15

В классическом случае уравнения, описывающие процессы в ЭЭС, являются однородными линейными (линеаризованными) дифференциальными уравнениями и имеют вид [5, 6]

—¹ = a ii x i + a i2 X 2 +.......... + a in X n ;

dt

= a 2i x i + a 22 X 2+.......... + a 2n x n ;                                            (3)

dt dxn

= a n1 x 1 + a n2 x 2 + ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ + a nn x n ;

либо в матричной форме x = Ax, , (4) где a11 a12..... ....a1n A= a21 a22.... .....a2n (5) an1 an2.... ......... a .....ann и хт = [x1, x2, .., xn]T - транспонированный вектор переменных состояния.

Для определения устойчивости (4) используем метод Ляпунова и зададим функцию в виде положительно определенной квадратичной формы

V(x)=x^TQx, или V = £ q ,j^xi^xj .

М=1

Производная этой функции dV d(xTQx) --=------ dt dt

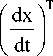
Qx + x T Q^—) =

I dt J

= (Ax) T Qx + x T QAx = x ^T A T Qx + x T QAx = = x^T (A T Q + QA) x.

Потребуем, чтобы функция Ляпунова удовлетворяла требованию

dV dt

- W ,

где W = xTCx - произвольная положительно определенная симметрическая матрица.

Приравнивая выражения (10) и (11), получим уравнение

A T Q+QA = -С.

Уравнение (9), называемое матричным уравнением Ляпунова, обеспечивает условие устойчивости, если одновременно выполняются неравенства V > 0 и V < 0 в некоторой области пространства переменных (x i , Х 2 , -, х_п), включающей начало координат [6].

Заметим, что обе матрицы Q и C симметричны. Действительно, если матрица Q симметрична, т. е. QT = Q, то

CT = - (ATQ+QA)T = -QTA - ATQ = - (ATQ+QA)=C (10)

и, следовательно, матрица C симметрична.

Функции (10), где Q - положительно определенная симметрическая матрица, удовлетворяющая условиям теоремы Ляпунова, называются квадратичными функциями Ляпунова. Теорема Ляпунова сводит проверку устойчивости исследуемой системы к решению линейного матричного уравнения. Так как матрица Q симметрична, то уравнение Ляпунова эквивалентно системе n(n+1)/2 линейных алгебраических уравнений. При большой размерности матрицы A решение такой системы занимает меньше времени, чем вычисление характеристического многочлена матрицы A [6].

Согласно теореме Сильвестра [1, 5], положительность главных диагональных миноров матрицы коэффициентов Q квадратичной формы (3) является необходимым и достаточным условием для устойчивости рассматриваемой системы при малых возмущениях q11

q12 q13

^Q = 4 21

q 22 q 23 >  ⁰ ,

q31  q32 q33

т.е.

q11   q12 ... q1n

Δ Л1 =q 11 >0, Δ Л2 =

^q 11

^q 21

> 0.

qn1  qn2 ... qnn

Анализ нарушения условия А _Л1=д₁₁>0 показывает все виды нарушения устойчивости электрической системы (апериодическое нарушение, самовозбуждение, самораскачивание) [6].

Линеаризованные уравнения простейшей ЭЭС при наличии на синхронном генераторе автоматических регуляторов возбуждения (АРВ) пропорционального или сильного воздействия имеют вид [4, 6]:

– уравнение относительного движения ротора синхронной машины:

Τ j (d²∆δ/dt)= – Ρ d (d∆δ/dt) – ∆Ρ;

– уравнение переходных процессов в обмотке возбуждения:

Τ d0 (∆Ε′ q /dt)= ∆Ε qe – ∆Ε q ;

– уравнение в обмотке возбуждения возбудителя:

T e (∆Ε qe /dt)=k e ∆e-∆Ε qe ;

– уравнение усилительного элемента:

T y (∆e/dt)=k y ∆u-∆e;

– уравнение измерительного элемента:

T И (d∆u/dt)=k u ∆u г -∆u;

– уравнение, отражающее влияние АРВ:

∆е = ∑ (k 0Пj ∆П j +k 1Пj (d∆П j /dt)+k 2Пj (d²∆П j /dt²);

j здесь – Τj, Τd0, Τe, ΤУ, ΤИ – постоянные инерции агрегата, постоянные времени, соответственно – обмотки возбуждения при разомкнутой обмотке статора, возбудителя, усилительного элемента, преобразовательного и измерительного элементов (ТИ = ТП); ∆δ, ∆Ε′q, ∆Εq , ∆Εqe , ∆е, ∆u, ∆uг – отклонения угла нагрузки, переходной э.д.с., э.д.с. холостого хода, э.д.с. на кольцах ротора, напряжения на обкладках возбудителя и напряжения на шинах генератора; ∆Пj – параметры режима, по которым осуществляется регулирование возбуждения генератора; Pd – демпферный коэффициент; k0Пj, k1Пj, k2Пj – коэффициенты усиления по каналам регулирования АРВ, соответственно – по отклонению, по первой и второй производным параметров режима. Отклонения регулируемого параметра режима генератора или системы определяют по соотношению

∆П j =(dП j /dδ)∆δ+(∆П j /dΕ q )∆Ε q .

Расчетная часть

Рассмотрим совместное применение уравнений узлового напряжения и функции Ляпунова в квадратичной форме на примере трехузловой схемы (рис. 1). В качестве балансирующего выберем нулевой узел, первый и третий узлы являются генерирующими, второй узел – нагрузочный.

Анализ статической устойчивости сложной ЭЭС проведем на основе известных допущений:

– при вычислении синхронизирующей мощности какого-либо из генераторов углы роторов всех остальных генераторов остаются неизменными. При этом мощности всех генераторов системы изменяются;

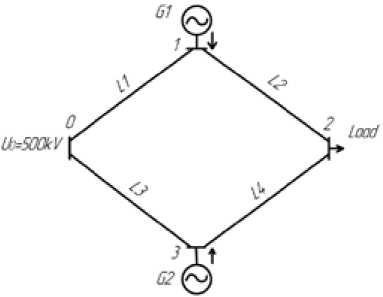
Рис. 1. Принципиальная схема трехузловой электрической системы

Fig. 1. Schematic diagram of a three-node electrical system

– предположим э.д.с. генераторов постоянными для заданного режима, параметры схемы замещения электрической системы и нагрузок постоянны, при этом активные составляющие комплексных сопротивлений не учитываются (r = 0);

– в установившемся режиме работы сложной системы мощности машин могут быть выражены через собственные и взаимные проводимости ветвей схемы замещения электрической системы, которые также считаются постоянными [3].

Как известно, для исследования статической устойчивости сложных систем пользуются позиционной математической моделью ЭЭС, имеющей вид:

– система дифференциальных уравнений относительного движения роторов синхрон- ных генераторов:

d ² δ 1      d δ 1

- P₁( δ ₁₂, δ ₁₃,... δ _1n);

T j1 _{dt 2} + P d1 _dt = P 10

d ² δ 2      d δ 2

- P 2 ( δ 12 , δ 13 ,... δ 1n );

T j2 _{dt 2} + P d2 _dt = P 20

T jn ^d _d ^δ _t2 ⁿ + P dn ^d _d ^δ _t ⁿ = P n0 - P n ( δ 12 , δ 13 ,... δ 1n );

– уравнения мощностей синхронных генераторов, выраженные через собственные и взаимные проводимости ветвей схемы замещения:

P 1 = E² 1 y 11 sin α 11 +E 1 E 2 y 12 sin( δ 12 - α 12 )+…+E 1 E n y 1n sin( δ 1n - α 1n ),

P 2 = E² 2 y 22 sin α 22 + E 1 E 2 y 12 sin( δ 12 - α 12 )+…+ E 2 E n y 2n sin( δ 2n - α 2n ),

n

Pn = E2nynnsinαnn+∑EiE j yijsin(δij-αij), i≠j где δi и δij – абсолютные и относительные углы нагрузки генераторов; Еi – электродвижущие силы генераторов; Tj – постоянные инерции агрегатов; Pdi – эквивалентные демпферные ко-– 935 – эффициенты генераторов; Pi – электромагнитные мощности синхронных генераторов; yii, yij – собственные и взаимные проводимости системы; αii и αij – соответствующие дополняющие углы [3, 11].

Ниже приведены исходные данные и параметры сложной электрической системы (рис. 1). Параметры узлов:

G1: P G1 =300 МВт; cosφ G1 =0.8; U G1 =500 кВ; T j1 =6 c.; x d1 =1.907; x^' d1 =0.278.

G2: P G2 =200 МВт; cosφ G2 =0.8; U G2 =500 кВ; T j2 =5.4 c.; x d2 =1.915; x^' d2 =0.275.

Узлы соединены между собой соответствующими воздушными линиями питания L1-L4.

• L1: U L1 =500 кВ; ℓ L1 =195 км; r 0 =0.0397 Ом/км; x 0 =0.31 Ом/км.

L2: U L2 =500 кВ; ℓ L2 =115 км; r 0 =0.0362 Ом/км; x 0 =0.306 Ом/км.

L3: UL3=500 кВ; ℓL3=180 км; r0=0.0397 Ом/км; x0=0.31 Ом/км.

L4: U L4 =500 кВ; ℓ L4 =175 км; r 0 =0.0397 Ом/км; x 0 =0.31 Ом/км.

Параметры нагрузочного узла:

P Load =600 МВт; cosφ Load =0.88; U Load =500 кВ.

Генераторы оснащены автоматическими регуляторами возбуждения сильного действия, реагирующими на отклонение и первую производную угла, а также на отклонение напряжения. Выполним расчет установившегося режима и проверим положительность первого минора q11 матрицы квадратичной формы Q для генерирующих узлов.

Результаты расчета установившегося режима:

U ^& ₁ = 505,2e^j15oкВ, U ^& ₂ = 496,2e^j34oкВ, U ^& ₃ = 509,8e^j23oкВ.

Затем, используя полученные данные, решим уравнение функции Ляпунова в квадратичной форме относительно указанных выше систем уравнений (5).

На рис. 2 отражено изменение первого диагонального минимума q11 матрицы Q функции Ляпунова в квадратичной форме, показывающий предел передачи по статической устойчивости.

Расчет производили с утяжелением режима – постепенным увеличением нагрузки PLoad = 150 МВт до PLoad max = 200 МВт, что приводит к увеличению угла до δcr = 138o.

Выводы

На основе исследований были получены два важных результата.

• 1.    Устойчивость электрической системы при малых отклонениях характеризуется положительностью первого минора матрицы квадратичной формы q 11 > 0 функции Ляпунова в квадратичной форме. Этот критерий называется упрощенным [3, 11], так как его положительность определяет положительность высших миноров матрицы. Важно, что условие q 11 >0 содержит теоретически известные типы нарушения устойчивости электрической системы и, следовательно, как необходимые, так и достаточные условия устойчивости.

• 2.    Аналитически определяется i-й генератор сложной электрической системы, первым приближающийся к пределу устойчивости:

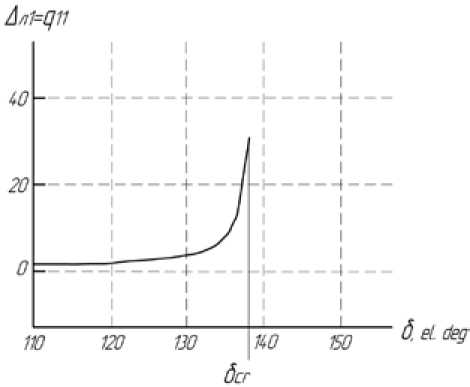
Рис. 2. Характер изменения первого диагонального минора q 11 матрицы Q функции Ляпунова в квадратичной форме

Fig. 2. The character of the change of the first diagonal minor q 11 of the matrix Q of the Lyapunov`s function in quadratic form

dq11j

→ max, dП , где П – какой-либо параметр.

Отличительной особенностью этого подхода было разрешение уравнений состояния системы относительно абсолютных углов в отличие от традиционных уравнений системы, составленных по взаимным углам [3, 11]. Этот подход упрощает изучение переходных режимов электрических систем, в том числе при анализе их статической устойчивости.

По мнению авторов, исследования малых колебаний электрической системы на основе функций Ляпунова в квадратичной форме должны быть разработаны и проведены по направлениям:

• –    усовершенствование модели уравнений узловых напряжений для совместного применения с функцией Ляпунова в квадратичной форме;

• –    разработка более точной модели электрической системы;

• –    разработка матричных методов для совокупного и взаимосвязанного оптимального управления между подстанциями и станциями электрической системы;

• –    разработка алгоритма и модели для оптимального управления, оценки и синтеза соответствующих законов управления ЭЭС при вероятностном характере исходной информации.