Исследование структуры сложных поверхностей деталей после дробеструйной обработки

EDN: ORUCBG

Структурный анализ поверхности занимает важное место в оценке качества поверхности деталей машин. Основой в оценке структуры лежит компьютерная обработка изображений различной природы. Широкое применение компьютерных методов структурного анализа нашли в материаловедении, медицине, криминалистике, при обработке изображений земной поверхности, полученных из космоса и аэрофотосъёмкой, а также в ряде других областей человеческой деятельности. К основным задачам структурного анализа относятся : выбор и формирование признаков, описывающих структурные различия; выделение и сегментация структур; классификация структур ; идентификация структур. Установлено, что в настоящее время не существует чёткого математического определения понятия структуры. В связи с этим методы описания структур и их различия, как правило, разрабатываются эвристически отдельно для каждого конкретного случая. В работах [1-3] и ряде зарубежных отечественных авторов представлены различные подходы к математическому описанию структур и методам их идентификации.

Для аналитического описания структур применяется ряд математических моделей. Среди них известны Time-series модель, ячеистая модель, синтаксические структурные модели, двумерная модель случайного марковского поля. Эти модели обычно применяются для воспроизводства внешнего вида структуры.

Для описания структуры изображения и её количественной оценки достаточно часто применяется метод, основанные на измерении пространственной частоты.

Системный анализ показал, что с точки зрения минимизации временных затрат при их реализации наиболее перспективным является использование метода измерения пространственных частот микрорельефа поверхностей. К группе частотных методов относится и метод цифровых преобразований, при котором в качестве характеристики структуры используется количество перепадов яркости на единицу площади изображения.

В нашей работе применен метод описание структуры с помощью автокорреляционной функции. Развитие данного метода связано с решением задач распознавания микрорельефов механически обработанных сложных поверхностей непосредственно в производственных условиях.

Многочисленными исследованиями установлено существенное, а в некоторых случаях и определяющее воздействие структуры рабочих поверхностей деталей взлетно-посадочных устройств на их надёжность и долговечность при эксплуатации [4-6].

В работе был применен оптико-электронный метод исследования, основанный на разработке теоретических основ реализации нового метода идентификации микронеровностей поверхности деталей. Сущность разработанного метода заключается в сравнении изображения структуры анализируемой поверхности с изображениями структур эталонных поверхностей, для которых заранее определены параметры шероховатости по стандартным методикам, например с помощью профилографа. В результате сравнения определяется (с заданной вероятностью) соответствие изображения структуры образцовой поверхности изображению структуры исследуемой поверхности. На основе этого ана- лиза было установлено, что поставленная задача может быть решена с использованием метода согласованной фильтрации. В работе было принято предположение, что входное изображение исследуемой поверхности x(n1, n2) обрабатывается линейной дискретной системой. В этом случае задача идентификации двумерного сигнала определённой формы решается с помощью согласованного с сигналом двумерного пространственного фильтра, отклик которого описывается выражением

∞∞

У ( n l ’ n 2⁾ = ^ 2 u ( k l ’k 2⁾ ^ ^k l ^— ( n l ^— n 01 ), k 2 ^— ( n 2 ^{— n} 02 )], k 1 =—^ k ₂ =—^

(1) которое представляет собой двумерную свёртку сигнала u ( k ^ , k 2) и импульсной характеристики фильтра x [ k ₁ — ( n — n _0l), k ₂ — ( n ₂— n ₀₂)] . При этом импульсная характеристика фильтра получается из ожидаемого двумерного сигнала путём его зеркального отражения относительно координатных осей n и n 2 , и смещения отражённого сигнала в сторону исходного на П 01, П 02 отсчётов. Выходной сигнал y ( n1 , n ₂) будет пропорционален автокорреляционной функции двумерного входного сигнала и будет достигнуто максимальное отношение сигнала к помехе на выходе фильтра. Разработан метод обработки изображения анализируемой поверхности для получения автокорреляционной функции, представленный на рисунке 1.

При каждом совмещении эталона U ( n , П 2 ) и текущего фрагмента полутонового изображения X ( n , n 2 ) подсчитывается коэффициент корреляции по известной формуле [6].

Л 1— 1 у н

ZZ ^{( m (} n l ’ n 2 ^{) —} m u ^{) - (} xnn l ^— k l ’ n 2 ^{— k} 2 ^{) —} m x ⁾ r xy ( k l ’ k 2 ) =       --------------------------------------------,

0 ^- ° ₂

где ( n , n 2 ) индексы элементов эталонного окна, ( k 1 , k ₂) - координаты эталона внутри зоны поиска K 1 х K ₂, а < 7 1 и < 7 "₂ - средние квадратические отклонения величин u ( n 1 , n ₂ ) и X ( n 1 , n 2 ) от их математических ожиданий m_u и m_x соответственно. Закончив вычисление коэффициентов корреляции в первой полосе, задаётся следующая полоса того же формата, что и предыдущая, но смещённая вниз на один пиксель. В этой полосе по центру задаётся новый эталон с теми же размерами, что и предыдущий, и выполняются те же самые действия и.т.д. После обработки всего изображения в запоминающем устройстве будет сформирована матрица M 1 х M ₂ коэффициентов корреляции или двумерная автокорреляционная функция. Анализируя выражение (2), можно отметить, что его числитель и знаменатель представляют из себя суммы произведений сигналов x ( n 1 , n ₂) и u ( n 1 , n ₂) . Следовательно, эти сигналы будут подвержены мультипликативному воздействию функции влияния f _зл ( Д ф , д а ).

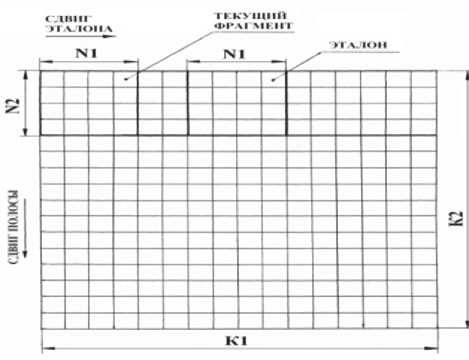
Рис. 1. Схема перемещения эталона

2 ^« п ^, П 2 ) — m, ) - f.„ ( Д Ф ,Д а ) - ( x ( ^— k l, П 2 — k J — m , ) - f ( Д ф ,д а ) r" ^(A’ k ²⁾ =                  o l - f . ( Д Ф, Да ) О 2 - f , ( Д Ф .Д а )                 '

Как видно из приведённого выражения, его структура соответствует структуре выражения (1) и функции влияния сокращаются. Следовательно, функцию (3) можно рассматривать как частный случай отношения (1) и утверждать, что она обладает искомым компенсационным свойством для устранения дополнительной погрешности, возникающей при оценке параметров микрорельефа непосредственно по видеосигналу, не требуя при этом введения дополнительной аппаратуры.

МЕТОДЫ ИССЛЕДОВАНИЯ

В исходном полутоновом кадре формата K 1 х K 2 пикселей, начиная с первой строки, выделяется полоса шириной в N ₂ пикселей. По центру этой полосы задаётся эталон размером N 1 х N ₂ пикселей. Затем эталон, начиная с крайней левой позиции, перемещается по выделенной полосе с шагом в 1 пиксель.

Для проведения исследований поверхности деталей взлетно-посадочных устройств был разработан переносной оптико-электронный комплекс для бесконтактного контроля геометрии, размеров и качества поверхности различных деталей в режиме 2D, представленный на рис.2. Комплекс обеспечен ноутбуком ( персональным компьютером), для которого в процес- се исследования разрабатывались специальные алгоритмы и программы. В качестве видеокамеры использовалась камера DIGITAL CAMERA Computar ZC-F11CH3, на выходе которой формировались чёрно-белые изображения заданного формата.

Мощность светового потока, падающего на исследуемую поверхность, в проведённых исследованиях изменялась варьированием напряжения питания лампы накаливания мощностью P = 60 Вт и U = 36 В . Питание подавалось от стабилизированного источника постоянного напряжения. Измерение освещённости исследуемой поверхности производилось люксметром марки 1016М, который располагался перпендикулярно падающему световому потоку . При этом площадь светового пятна на поверхности люксметра составляла S =0,00126 м² . Мощность светового потока Ф (в люменах) определялась с помощью известного соотношения Ф = E·S , где E – освещённость, измеряемая в люксах.

Исследования структуры поверхности производилось после дробеструйной обработки деталей из титанового сплава ВТ8 на станках с ЧПУ. Деталь может не сниматься со станка или находиться рядом на столике, переносная видеокамера устанавливается на магнитной опоре над измеряемой поверхностью. Видеокамера передает цифровой сигнал в программный комплекс, который обрабатывает полученный сигнал определяя основные параметры структуры поверхности: среднюю амплитуду автокорреляционной функции Аср, средний шаг автокорреляционной функции Тср и их ошибки. Для сравнения результатов измерения структуры оптическим комплексом , изготавливались образцы –свидетели, которые обрабатывались на станке с ЧПУ с различными режимами дро- беструйной обработки. Затем на образцах-свидетелях определялись стандартные параметры шероховатости поверхности на профилографе модели SJ - 201P.. Найденные значения среднеарифметического отклонения профиля представляют собой средние значения, вычисленные по 10 измерениям для каждого образца. Затем определялись структурные параметры с помощью оптико-электронной системы. Анализируемая поверхность эталонных образцов имела размер 3 X 2,5мм, что соответствовало от 800 до 1000 профилей. Световой поток мощностью 600.10–3 лм падал на исследуемую поверхность под углом 45°. Формат видеокадра, записываемого в память компьютера, составлял 320 х 240 пикселей.

На рисунке 3 показана последовательность определения структурных параметров поверхности в следующим порядке: на реальной поверхности выделялся анализируемый участок (рис. 3а), затем, применяя разработанную методику, преобразуем реальную поверхность в бинарное изображение (рис. 3б) , применяя сканирующую методику движения эталона получаем реальную корреляционную поверхность (рис. 3в) и ее бинарное поле (рис. 3г). Производится статистический анализ полученных результатов, и определяются параметры структуры поверхности.

Программа построена таким образом, что можно построить корреляционный профиль (рис. 4), который чем-то напоминает профилограмму поверхности.

На структурные параметры поверхности оказывает большое влияние скорость дроби в факеле дробеструйной обработки. На рис. 5 показана методика определения структурных параметров поверхности при Vш =70 м/с

Рис. 2. Оптико-электронный комплекс для измерения параметров структуры сложных поверхностей деталей взлетно-посадочных устройств

а                                  б

в

г

Рис. 3. Параметры структуры поверхности образца – свидетеля обработанного дробью диаметром 0,6 мм с режимами: скорость движения шариков в факеле V_ш =60 м/с, время обработки т = 5- 20 мин, а –электронная фотография, б – бинарное изображение, в – корреляционное изображение, г – бинарное корреляционное изображение

На рис. 6 показаны корреляграммы поверхности образцовm обработанных дробью.

В этом случае можно предложить следующий общий алгоритм оценки микрогеометрии по параметрам структуры.

• 1.    Для измеряемой шероховатости промышленного изделия изготавливаются по той же самой технологии образцы- свидетели поверхности с различной шероховатостью, определяемой стандартными, ГОСТовскими методами с помощью образцового средства измерения.

• 2.    С помощью оптико-электронного измерительного средства формируются изображения образцовых поверхностей полученных поверхностей, по ним вычисляются корреляционные функции и строится аналитическая зависимость Ra = f ( А_ср), Ra = f ( Т_ср)

• 4.    Для заданной вероятности распознавания строится доверительный интервал I _p = f (А_ср), I _p = f ( Т_ср), в который попадает случайная величина А_ср и Т_ср.

• 5.    Для анализируемой поверхности с неизвестной шероховатостью, сформированной по той же самой технологии, с помощью

• 6.    Используя полученные зависимости Ra = f (А ср ) и I p = ^f (А ср ),

оптико-электронного измерительного средства формируется изображение поверхно- сти и определяется Аср и Тср корреляционной функции.

Ra = f (Т_ср) и I _p = f (Т_ср) определяются Ra, Ra_min, Ra_max.

По результатам структурного анализа эта- лонов шероховатости поверхности после дробеструйной обработки получены зависимости по влиянию параметров структуры Аср и Тср на параметр Ra поверхности. Отмеченное обстоятельство объясняется возрастающим влиянием регулярной компоненты в формировании микрорельефа исследуемых поверхностей.

Полученные зависимости Ra = f(А_ср) могут быть аналитически представлены выражениями вида Ra = К ^. А_ср – В.

В частности, для проведенных исследований по дробеструйной обработке аналитическое выражение будет иметь вид:

Ra = 0,12 ^. А_ср – 1,4 ,мкм; (4) Rz = Т_ср² / 8 ^. r_ш мкм. (5)

Коррелярограммы поверхности	Параметры структуры
А 1.0 ■■ |о.75" 0.25 е го 0         ---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------1---------------> 0     40    80    120 160 200 240 280 320 360 400 440 480 пиксели	А ср = 19,8 Т ср =14,3 ПК или Т ср =71,5мкм
1
А гНМйЙйШ# Q --------------1-------------1-------------:-------------1-------------1-------------:-------------1-------------1-------------:-------------1-------------:-------------1-------------5 0    40    80    120 160 200 240 280 320 360 400 440 480 пиксели	А ср = 20,5 Т ср =16,7 ПК или Т ср =83,5мкм
2 Л ’r ANMVjw^ ° 0     40    80    120 160 200 240 280 320 360 400 440 480 пиксели	А ср = 22 Т ср =20,8 ПК или Тср =104 мкм
3

А ср = 23,2

Т_С р =25,0 ПК или

Тср =125 мкм

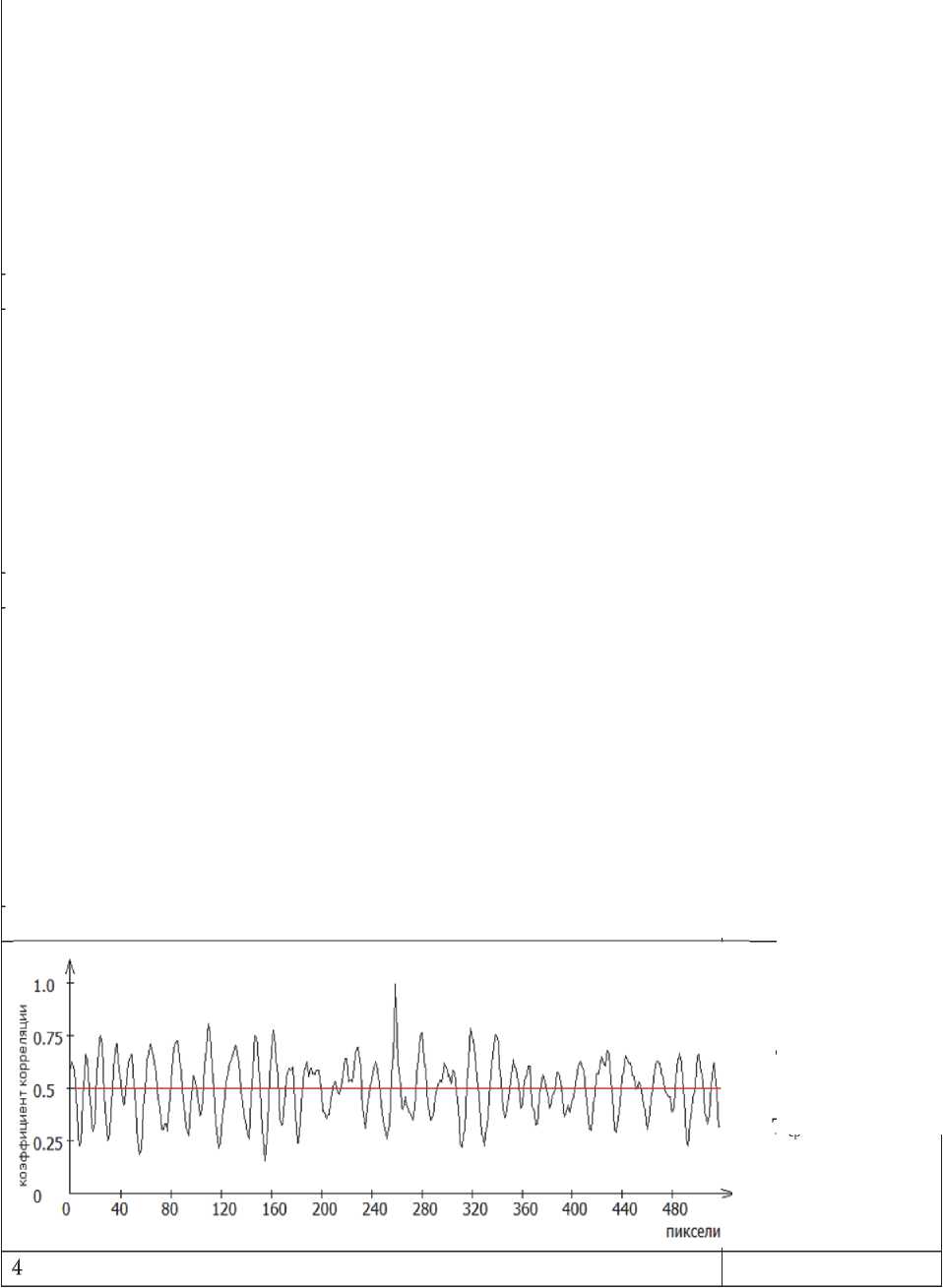
Рис. 4. Коррелялограммы поверхности образцов-свидетелей после дробеструйной обработки шариками d= 0,6 мм со скоростью движения шариков в факеле V_ш =60 м/с с режимами τ = 20 мин (1), τ = 15 мин (2), τ = 10 мин (3), τ = 5 мин (4)

в                                    г

Рис. 5. Параметры структуры поверхности образца – свидетеля обработанного дробью диаметром 0,6 мм с режимами: скорость движения шариков в факеле V_ш =70 м/с , время обработки τ = 5- 20 мин, а – электронная фотография, б – бинарное изображение, в – корреляционное изображение, г – бинарное корреляционное изображение

Подставив экспериментальные значения в аналитические зависимости, получим значения Ra, приведенные в табл.1

Для сравнения результатов расчета по формулам 1 и 2 .нужно преобразовать параметр Rz

• в Ra = Rz / 4 мкм

Анализ полученных зависимостей также показал, что для поверхностей с дробеструйной обработкой наблюдается повышение параметра Ra при увеличении скорости шариков с факеле

Таблица 1. Параметры обработки

Параметры структуры поверхности
А ср	Ra, мкм	Т ср , ПК	Т ср , мкм	Rz, мкм
Скорость движения шариков в факеле Vш =60 м/с
19,8	0.96	14,3	71,5	4,16
22,5	1,3	16,7	83,5	5.68
26,0	1.72	20,8	94,0	7,2
28,2	1.98	22	110,0	9,6
Скорость движения шариков в факеле V ш =70 м/с
17,8	0,74	11,7	61,4	3,08
19,2	0,91	12,4	68,5	3,84
20,3	1,04	13,5	72,5	4,28
21,4	1,2	16,7	81,5	4,92

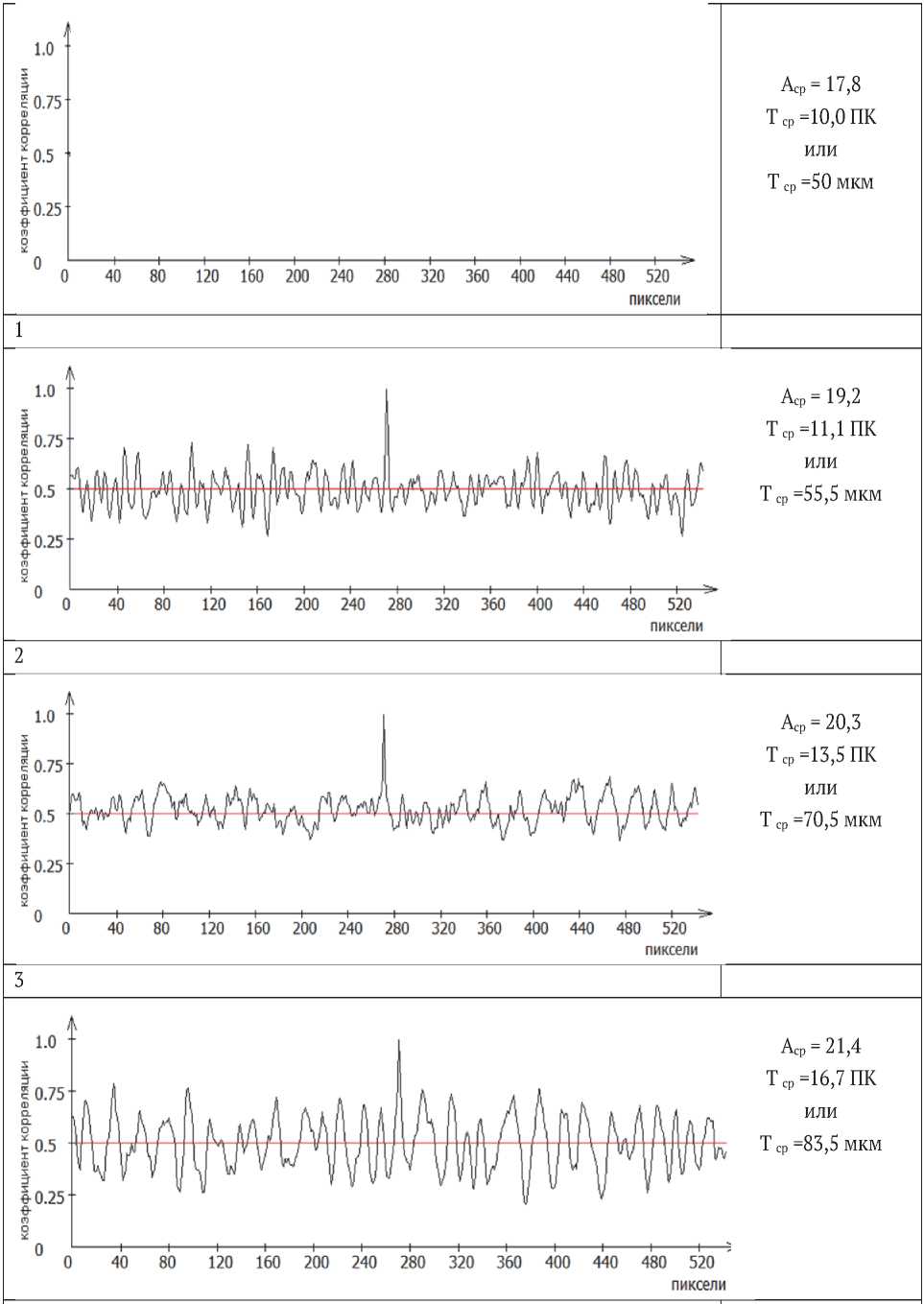
Рис. 6. Коррелялограммы поверхности образцов-свидетелей после дробеструйной обработки шариками d= 0,6 мм со скоростью движения шариков в факеле V_ш =70 м/с с режимами τ = 20 мин (1), τ = 15 мин (2), τ = 10 мин (3), τ = 5 мин (4)

1
	^WWV vyvywvvV

дробеструйной установке и снижение параметров структуры А ср .и Т ср . при увеличении времени обработки. Отмеченное обстоятельство объясняется возрастающим влиянием регулярной компоненты в формировании микрорельефа исследуемых поверхностей.