Исследование структуры УНЧ-колебаний вблизи плазмопаузы при наличии в магнитосферной плазме тяжелых ионов

Геомагнитные пульсации диапазона Рс1 (0.1–5 Гц), как обычно считается, являются волновыми пакетами, бегущими между магнитосопряженными точками ионосферы и генерируемыми ионно-циклотронной неустойчивостью [Гульельми, 1979; Demekhov, 2007]. Эти пульсации часто наблюдаются вблизи внутренней границы плазмосферы [Fraser, Nguyen, 2001; Engebretson et al., 2002]. На плазмопаузе имеется минимум скорости альфвеновской волны, благодаря чему плазмопауза является наиболее удобной областью для возбуждения и распространения этих волн.

Дмитриенко и Мазур [Dmitrienko, Mazur, 1985; 1992] показали, что вблизи области плазмопаузы может сформироваться резонатор для Рс1 поперек силовых линий. Волновой пакет Рс1 является суперпозицией собственных мод резонатора.

Важно учитывать наличие тяжелых ионов в плазме, поскольку их может быть так же много, как и протонов [Yang et al., 2010]. Впервые структура УНЧ-волн в случае наличия тяжелых ионов в магнитосфере была рассмотрена в работе [Гульельми, 1967]. Более подробно их структура была рассмотрена в работах [Rauch, Roux, 1982; Guglielmi et al., 2000, 2001; Guglielmi, Kangas, 2007; Гульельми, 2007; Klimushkin et al., 2010; Мариловцева и др., 2010; Михайлова, 2011; Гульельми, Потапов, 2012]. Было показано, что на экваториальной части силовой линии вдоль направления магнитного поля может быть сформирован резонатор. Частота волны определяется собственными частотами резонатора. Результаты некоторых наблюдений заставляют усомниться в модели бегущего волнового пакета, но не противоречат существованию экваториального резонатора [Mursula, 2007; Пилипенко и др., 2012].

Как уже было упомянуто выше, предполагается, что волны Рс1 генерируются ионно-циклотронной неустойчивостью [Demekhov, 2007]. Условием существования такой неустойчивости является квази-продольное распространение волны кц>>к±. Малость поперечной компоненты волнового вектора обусловлена малостью азимутального волнового числа (m=0) и малостью радиальной компоненты волнового вектора в поперечном направлении, поскольку поперек силовых линий волны заперты в резонаторе вблизи центра плазмопаузы [Dmitrienko, Mazur, 1992]. Глобальные поперечная и продольная структуры этих волн с учетом наличия в плазме тяжелых ионов являются предметом изучения в данной статье. Для исследования структуры колебаний используется ВКБ-приближение по продольной координате. В работе применяется аксиально-симметричная модель магнитосферы и учитывается кривизна силовых линий магнитного поля. Частота волны предполагается порядка гирочастоты тяжелых ионов, так как в земной магнитосфере основную долю примеси тяжелых ионов составляют ионы кислорода, а их гирочастота одного порядка с частотой пульсаций Рс1.

Резонаторы

Для холодной однородной плазмы, принимая во внимание ограниченность отношения частоты волны к циклотронной частоте, можно получить дисперсионное соотношение для УНЧ-мод:

I ГО /2 11® л 2 1 2 I ® 2

I р"£^-kw II р"£^-k -kр = р"п , (1)

где го - частота волны, с - скорость света, е _± и п — диагональный и недиагональный элементы тензора диэлектрической проницаемости, к ц и к _± - продольная и поперечная компоненты волнового вектора [Swanson, 1989].

Дисперсионное соотношение (1) принимает различные формы в зависимости от того, какое приближение рассматривается для изучения распространения волн – квазипродольное или квази-поперечное. Так, в работах [Guglielmi et al., 2000, 2001] используется квазипродольное приближение. В таком случае к2 / k2 ^ 0, а уравнение (1) принимает вид to2

"Г 6

—

A2   „4

к 2 I ~-  2

k I - 4 ^ '

CO 2

Два решения этого уравнения k |2_± -—( е_±±п ) соответствуют лево- и правополяризованным модам. В случае левополяризованной волны (знак «плюс») при наличии в магнитосферной плазме легких (протонов) и тяжелых ионов, k 2 представим в параболическом виде. Зависимость k 2 от координаты, направленной вдоль силовой линии, представлена на рис. 1.

На рис. 1 видно, что при достижении некоторых точек функция k 2 обращается в нуль, за которым следует область непрозрачности ( k 2 <  0 ) . Таким образом, волна оказывается запертой вблизи экватора в продольном направлении.

В квазипоперечном приближении ( k 2 / k 2 >>  1 ) дисперсионное соотношение (1) переходит в

2                     2    4

to            п ю

e± —k - — FZ’ cc этот случай описан в работах [Klimushkin et al., 2010; Мариловцева и др., 2010]. Учитывая большую величину k2 ’ можно получить выражение для продольной компоненты вектора

, 2 _ k - 2 8±.

В этом случае также имеются точки, в которых k 2 обращается в нуль, соответственно, формируется резонатор в окрестности экватора. Предполагается, что области непрозрачности достаточно широкие, поэтому волна не проникает в ионосферу, а оказывается запертой в резонаторе. В случае квазипоперечного приближения существует только левополя-ризованная волна.

Кроме экваториального резонатора представляет интерес волновод, локализованный вблизи плазмопау-зы [Dmitrienko, Mazur, 1992]. Этот волновод форми-

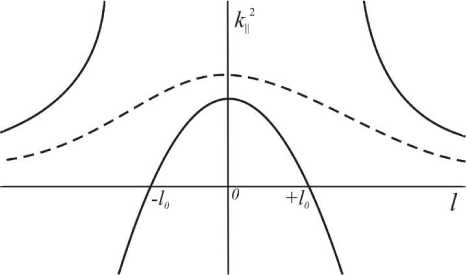
Рис. 1 . Схематичное изображение зависимости квадрата показателя преломления от продольной координаты. Сплошной кривой показана левополяризованная волна, штриховой – правополяризованная.

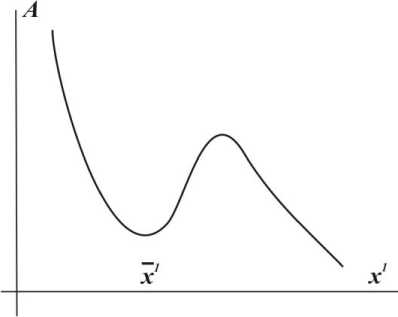
Рис. 2 . Схематичное представление профиля альфве-новской скорости в зависимости от координаты поперек силовых линий. В области плазмопаузы наблюдается минимум альфвеновской скорости.

руется благодаря минимуму альфвеновской скорости на плазмопаузе (см. рис. 2).

Итак, в рамках данной задачи волна оказывается запертой в волноводе поперек силовых линий и распространяется вдоль силовой линии, отражаясь от границ ионосфер разных полушарий. Примесь тяжелых ионов в плазме в этой задаче не учитывалась.

Возникает вопрос: а что же будет, если объединить все эти исследования? Как изменится глобальная структура волны, локализованной в волноводе вблизи плазмопаузы, если добавить в состав плазмы небольшую примесь тяжелых ионов? Данная работа посвящена поиску ответа на этот вопрос.

Система координат и основные уравнения

В рамках нашей задачи используется аксиальносимметричная модель магнитосферы. Вводится ортогональная система координат, ориентированная по полю {x1, x2, x3}, в которой координаты х1 и х2 являются радиальной и азимутальной координатами соответственно, а координата х3 направлена вдоль линий окружающего магнитного поля. Элемент длины в этой системе задается выражением dl2 - g (dr1)2 + g2 (dx2)2 + g3 (dx3)2.

Здесь g_f - g _;( г ¹, x ³) - диагональные элементы метрического тензора, g - g_xg₂g₃ — детерминант метрического тензора. Суммирование по повторяющемуся индексу не подразумевается. Физическая компонента вектора, измеряемая в евклидовой системе координат, выражается как a — Qj / ^g — g^ j i^J , нижние и верхние индексы означают ковариантные и контравариантные компоненты вектора соответственно (рис. 3).

Возмущения электромагнитного поля E задаются уравнением Максвелла to-ee-VxVxE, (2) c где to - частота волны, c - скорость света, s - тензор диэлектрической проницаемости, который имеет компоненты

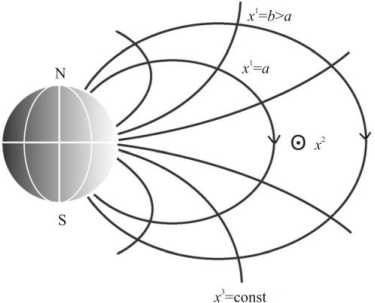
Рис. 3. Система координат.

E_a = ei ^{T ( x} 1 , x ³⁾.

Рассмотрим волны мелкомасштабно-неоднородные

вдоль координаты неоднородные вдоль

x3   и крупномасштабно- x1  [Dmitrienko, Mazur,  1985,

d E^ dT _

1992]. Это означает, что —a >>    . Следовательно, dx3 dx1

такое же неравенство справедливо и для фазы колеба- dT  dT _ ния —— >> ——-. Фазу можно представить в виде dx3     dx^

^ ( x ¹, x ³) = T ^{1 - 1)} ( x ³) + T ⁽⁰⁾ ( x ¹, x ³) + ...

^1=-»,

_e =    ^P    ₊    ^Q 2h

¹  Q 2p -ю ²   Q 2h -ю ²,

_ _    pe      cp      pp      Qchph n =----2-----2----2Г .

ю-Q   ю Qm - ю ю Q. - ю ce              cpch

Индекс означает порядок разложения по параметру λ || / l || , где λ || – продольная длина волны, которая много меньше, чем l || – продольный масштаб неоднородности среды. Обозначим

н _a ( x ¹, x ^з) = e ^{T (0)(} x ¹ , ^{x 3)}

.

Здесь Ω_р и Ω_с – плазменная и циклотронная частоты соответственно, а второй индекс означает частицу: p – протон, h – тяжелый ион, e – электрон [Glassmeier et al., 2003]. Для колебаний с азимутальным волновым числом m =0 можно получить систему уравнений

d g 2 d ^{dx 3} Л ⁸x³

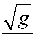
Ei +  2     e, Ei c2  g1

ю

- i "^ nV g 3 E 2 = 0,

Соответственно, величина H _α также представима как

H _a ( x ¹, x ³) = H a⁰⁾( x ¹, x ³) + H a 1) ( x ¹, x ³) + ... (5)

Функция H ⁽⁰⁾ ( x ¹, x ³) описывает поперечную структуру моды колебания, в то время как для нахождения продольной структуры необходимо учитывать и H ⁽¹⁾( x ¹, x ³) (см. ниже).

Таким образом, структура моды колебаний в ВКБ-приближении по продольной координате имеет вид

8 g 3 _LF .JL g1 8 F , ax1 V? 8x1 2 8x3 VF 8x3 2

+ <    e , E 2 + i < n    E,= 0.

c ² g ₂            c ²

Эту систему можно записать в матричном виде:

L E = 0,                                     (3)

где эрмитов оператор L ^ˆ имеет вид

, _;^d g 2 ^d . ю² Л_Р

L ¹¹ = 6x ³ v g dx ^{3 +} c² g i ^8± ’

L12 = ^- i   n V g ",

L =

21      12 , t _ d  g3  d , d  g1 d  , ю2Л r

²² d x ¹ ^J g d x¹ d x ³ ^J g dx³ c ²   g ₂   ¹ ’

E _a = H _a ( x ¹, x ³) ei ^{T ( - 1)},

Вводим

^{( - 1)}

k3( x3) =         , dx

тогда

T ^{( - 1)} = j k₃ ( x ³) dx ³.

В свою очередь, оператор L^ˆ системы (3) можно разложить следующим образом:

L. = LS^^0 + L1, где оператор Lˆ(0) задает систему уравнений, полученных в главном порядке ВКБ-приближения, а Lˆ(1) возникает при нахождении следующего порядка при учете функции H(1)(x1, x3). Оператор Lˆ(0) выглядит следующим образом:

а звездочка означает комплексное сопряжение.

Граничные условия определяются из условия, что при прохождении точек поворота (точки поворота ограничивают экваториальный резонатор) волна попадает в область непрозрачности и экспонен-

т(0) = ю Л. _g2_ ,2 11                e1           3 , c2 g1        g

Ro) • ^ю _ Г”

Ц2 =^- i —nV g 3 , c

f (0) _ f(0) *

^21 = ^12 ,

циально затухает, т. е. стремится к нулю при выходе за пределы резонатора.

В ВКБ-приближении волну можно представить в

f (0)₌ A '   . ^ю2 Л_Р        )

^L22   d x- v ? d x^{1 +}i c² g2 ^£1  v g^{k 3} J

виде

Оператор L^{ˆ (1)} задается в виде

Т (» = Л’? = ,A JL^iJL A_{— 9} А fAl g з 5 x³     d x³ g з     g з d x³ ’

A = L ? = 0.

Поперечная структура УНЧ-волн на плазмо-паузе

В общем виде система (3) приобретает вид

L⁰ h <°) + fro н (°> + ц о» н (1) = о.                (9)

Главный порядок ВКБ-приближения описывается первым слагаемым

/?" hот = о.                                  (io)

d ² H <⁰⁾ d x¹'

+^гот = 1 H 2 ⁰⁾ c

2 го 8_± c⁷ Hill

—

(j x ¹ — xx ¹ )² + k ² HH <⁰⁾ = — i n HH ²°),

CO2                      - где n = П. Выражая H(0) из первого уравнения c

(13) и подставляя во второе, получим уравнение

8 ² Hi <°> a^ ²

v 2    Г 2^2 _ ⁿ 2 ^ ²

° k ^x  X — ² ^ ² + k ²

где введены новые обозначения

HH ( ⁰⁾ = °,

Система (10) вместе с граничными условиями по координате x ¹ представляет собой задачу на собственные значения параметра k₃ = k ₃ ( x ³). Поскольку эта система содержит производную только по x ¹, функция H ⁽⁰⁾ ( x ¹, x ³) описывает поперечную структуру моды.

Мы рассматриваем диапазон частот Q ch < w << Q _cp, поэтому мы вправе использовать выражение

2r2

X ⁴ = -^{l 1 C} _T, = го

2    -^to kll     k\\     c2 =1,

c

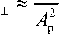
A ;

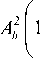
го ²

Q2

ch

Вблизи плазмопаузы радиальный профиль аль-фвеновской скорости ( А = B / ^4 пр , где р - плотность плазмы) имеет минимум. Значение величины 8 1 на плазмопаузе ( х¹ = х ¹) имеет максимум как функция x ¹ при фиксированном значении x ³. При отдалении от плазмопаузы значение функции 8 ₁ уменьшается, поэтому справедливо параболическое представление:

Л ^ ~ 1—1

Xq = x — x .

Собственным решением этой задачи является k 2 = k |2 ( x ³). Уравнение (14) сводится к уравнениям для глубокой и мелкой потенциальных ям при различных значениях n .

В статье [Leonovich, Mazur, 1993] была рассмотрена крупномасштабная неоднородность по координате x ³ и мелкомасштабная по x ¹. В этом случае решается продольная задача на собственные значения k 1 ( x 1 , го ). Такой способ применялся к рассмотрению колебаний типов Рс4, Рс5.

е_± ( x ¹, x ³) = е_± ( x ¹, x ³)

( x ¹ - x ^²

[ l '( x ³) ] ²

Здесь l ¹( x ³) – масштаб неоднородности по коорди- 1 ₃\ l . ( x ³) ₃

нате x 1; l\x ³) = —=-, где l_L ( x ³) - масштаб неод- 4^

нородности поперек магнитных оболочек. Изменением коэффициентов метрического тензора можно пренебречь, потому что рассматриваемые волны имеют область локализации меньше, чем масштаб неоднородности магнитосферы.

Переходя к физическим величинам, получаем систему уравнений, описывающих поперечную структуру:

Глубокая и мелкая потенциальные ямы

Уравнение (14) имеет вид уравнения Шредингера с потенциалом вида потенциальной ямы. Существуют два типа потенциальной ямы: глубокая и мелкая. Глубокая потенциальная яма отличается тем, что имеет несколько дискретных энергетических уровней, в то время как мелкая имеет только один уровень.

Если |^|<k, то уравнение (14) сводится к уравнению на функции параболического цилиндра. Решение этого уравнения известно. Оно описывает глубокую потенциальную яму:

а ² HH<⁰⁾ 5^ ²

q ² + k ² x ²

—

n ² X ²

k

а ² HH *⁰⁾

aq ²

= °.

Собственные функции такого уравнения q2

T H < ⁰⁾ = T H < ^0> = / ² He n (V2q) ,                   (16)

здесь He – полиномы Эрмита. Дискретный спектр собственных значений имеет вид

„ 2

— E Я (0)

2 = 1 ^H 1

c

гот >( x - x ')^{2 +} k 2 c ^g 1A

x н у = i n Hi *⁰⁾,

X

1 (1

k(n) =n—ГГI n+tI.

X V

Если Xn >>  1 и X k^_n ) >>  1 при малых n , то первое уравнение системы (13) задает связь между радиальной и азимутальной компонентами электриче-

ского поля волны H (0) ® - iH ⁽⁰⁾. Колебания имеют левую круговую поляризацию и локализованы вблизи экваториальной области.

В противоположном случае, когда Xn <<  1 и X к ц <<  1, уравнение (14) имеет вид

_{1 3} i k ₃ ( x ³ ) dx ³

виде E_a — H_a ( x , x ) e с различными знаками k 3 (x 3 ) на точках поворота ( ± l ₀) Е _а ^ 0, тогда получаем условие квантования Бора–Зоммерфельда:

[^{1 0} к*■ ” ) ( x ³) dx ³ — л[ N + ¹ | ,

^{- 1 0}                    V 2)

2 ˆ (0)

^-^2- -§ ² Hr ⁽⁰ > = 0.                        (18)

д^ ^{2         2}

Это уравнение описывает потенциальный барьер мелкой ямы. Оно представляет собой сокращенную форму уравнения на функции параболического цилиндра. Мелкая потенциальная яма имеет только один энергетический уровень. Решение задается уравнением

Hr 2 ⁰⁾ = CD 1 (V2 5 ) , 2

где C=const , D_n ( x ) – функция Уиттекера (функция параболического цилиндра). Чтобы получить энергетический уровень мелкой потенциальной ямы, нужно проинтегрировать уравнение (14) [Ландау, Лифшиц, 2004]. Считается, что значение H ^ˆ мало меняется. Интегрирование производится по всей ширине резонатора. Так как точки поворота резонатора расположены далеко от экватора, то пределы интегрирования можно устремить к бесконечности. Таким образом, энергетический уровень мелкой потенциальной ямы

~2_ п² Г²(1/4)   4 6

k                ^п X .

8 Г2(3/4)

Видно, что в одном случае задача имеет дискретный набор собственных значений. Резонатор имеет вид глубокой потенциальной потенциальной ямы. В другом случае резонатор описывается уравнением для мелкой ямы. В мелкой потенциальной яме имеется только одна мода колебаний, и эта мода имеет линейную поляризацию.

где n и N – поперечное и продольное квантовые числа. Условием применимости правила квантования Бора–Зоммерфельда является большое значение волнового числа N, однако, как показывает практика, оно дает верный результат и для волновых чисел порядка единицы. В этом условии квантования k(n) (x3) зависит от координаты x3 и зависит от частоты to= го nN как от параметра. Отсюда может быть определена частота волны. Согласно выражению (17), продольная компонента волнового вектора может быть представлена в виде to       to      Юа/е । (1 kll   (x, to „N ) — —s±+ n--I « +-I.

c      c      c^ V

В работах [Guglielmi et al., 2007; Klimushkin et al., 2010] было показано существование экваториального резонатора, служащего резервуаром энергии для возбуждаемых в нем гармоник. Воспользуемся разложением для k2 в окрестности точки, где к2 — 0. Учитываем, что магнитное поле не постоянно вдоль силовой линии и представимо в виде в — Be

1 +

2 V R e L J

здесь B _E – величина магнитного поля на экваторе, R _E L – расстояние от центра Земли, выраженное в ее радиусах. Используя это представление и применяя условие квантования (23), получаем выражение для частоты:

Продольная структура УНЧ-волн на плазмо-паузе

Продольная структура волны не описывается в первом порядке используемого ВКБ-приближения. Необходимо использовать следующий порядок разложения по параметру Хц / | , чтобы получить продольную структуру. Следующий порядок определяется из выражения

L¹H ( ⁰⁾ + L⁽⁰⁾ H (1) — 0. (21)

Чтобы разрешить систему (21) и найти продольную структуру, необходимо найти функцию ¥ ⁽⁰⁾. Условие разрешимости системы может быть выражено как

1Hа0)+L® H, dx — 0, (22) где а, в — координаты, H(0) + - эрмитово сопряженная величина H(0) +. Чтобы воспользоваться граничными условиями, нужно взять суперпозицию волн в to, N —

1 + ^ Q._+ 3

+

ch

P p J

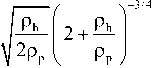
A ²

^ ch l 1 R E ^L

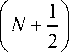
X

X

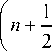
где p h и p p - плотности тяжелых ионов и протонов, ρ=ρ p +ρ h , A – альфвеновская скорость плазмы.

Частоты волн, возбуждаемых в резонаторе, квантованы. Частота волны зависит как от продольного

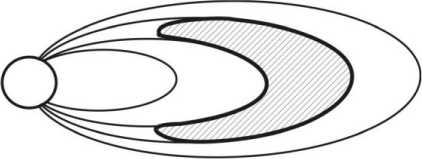
Рис. 4 . Мода, запертая в экваториальном резонаторе.

волнового числа N , так и от поперечного n . Поскольку все частоты возбуждаются одновременно, возникают биения, сходные по своей форме с формой Рс1-пульсаций. Из полученного выражения видно, что частота колебаний го близка по значению к частоте Ω сh , однако больше нее. Это согласуется с рассматриваемым диапазоном частот Q ch < го << О _cp,тем более что p h в нашем случае больше p p . Выражение (25) получено для волн, локализованных вблизи магнитного экватора. Поскольку ширина экваториального резонатора относительно небольшая, рост Ω_сh с удалением от экватора не оказывает существенного влияния на изменение частоты возбуждаемой гармоники.

Часть полученного спектра частот совпадает со спектром, полученным в работе [Guglielmi et al., 2000]:

го^ = f1 + ph^Qch+ 3 К—fN + -).

N ( P p J c ^h P p R e L I 2 J

Принципиальная разница между этими выражениями заключается в последнем слагаемом выражения (25), которое позволяет учесть кроме продольной структуры колебаний поперечную. Очевидно, что волны, возбуждаемые в резонаторе, имеют сложную структуру и их структура и частоты зависят от многих параметров (рис. 4).

Можно сделать некоторые численные оценки. Оценки сделаны для главной гармоники с волновы ми числами N= 0 и n= 0. При — ® 1.6, A=500 км/с pp

(на экваторе вблизи плазмопаузы альфвеновская скорость имеет минимальное значение), Ω_сh≈1 c^–1 , 1 1 ~ 10⁴ км [Dmitrienko, Mazur, 1992] частота нулевой гармоники го ₀=2.64 c^-1, точки поворота находятся на расстоянии l ₀=0.77 R _E от экватора. Согласно оценкам из работы [Klimushkin et al., 2010], точка резонанса, отграничивающая область непрозрачности от приионосферной области проводимости, находится на расстоянии l r =1.96 R E от экватора. Отсюда видно, что ширина области непрозрачности очень велика и колебания не могут проникать сквозь нее. Волна оказывается запертой в экваториальном волноводе.

Заключение

В настоящей статье были рассмотрены собственные волны в волноводе плазмопаузы в случае присутствия тяжелых ионов в плазме магнитосферы. Этот волновод появляется благодаря минимуму профиля альфвеновской скорости на плазмопаузе. Предполагается, что УНЧ-колебания распространяются между точками поворота резонатора вдоль силовой линии и используют различные магнитные оболочки в качестве границ в поперечном направлении.

На основании ВКБ-приближения по продольной координате были получены волновые уравнения для альфвеновских волн. Уравнения были решены с учетом того факта, что профиль альфвеновской скорости имеет минимум вблизи плазмопаузы, и было показано, что в приэкваториальной области резонатор опи- сывается при помощи модели глубокой потенциальной ямы. В этой области имеется дискретный набор собственных мод. В некоторых случаях волновод может определяться приближением мелкой потенциальной ямы. В этом случае было показано существование единственной собственной моды.

Было получено условие, которое определяет частоту волны. Так как продольное волновое число большое, множество различных гармоник могут возбуждаться одновременно. Резонатор ограничен точками поворота, таким образом, появляется стоячая волна. В результате формируются биения, имеющие форму, подобную структуре пульсаций Рс1.

До сих пор остается неисследованным вопрос о том, что происходит на торцах области, в которой заперта волна. Не ясно, имеют ли торцы округлую форму, как изображено на рис. 4, или какую-либо другую. От формы торцов зависит, каким образом происходит отражение волны в точках поворота. Не исследован пока и механизм отражения волны в точке поворота. Строго говоря, в нашем случае данные вопросы непринципиальны, так как механизм отражения волны не влияет на результаты, полученные в данной работе.

Следует отметить, что распространение УНЧ-волн в плазме при наличии в плазме ионов гелия было рассмотрено в работах [Young at al., 1981; Rauch, Roux, 1982]. В этих работах исследован случай кроссовера. В нашей же работе кроссовер отсутствует, поскольку возможно существование волны только одного типа поляризации.

Работа выполнялась при поддержке программы № 22 Президиума РАН, грантов РФФИ № 12-02-00031-а и № 12-05-00121-а. Автор выражает признательность Д.Ю. Климушкину за постановку задачи и многочисленные обсуждения, а также П.Н. Магеру за ценные замечания.