Исследование сушки натуральной кожи методом регулярного режима и обобщенными комплексными переменными
Автор: Ольшанский А.И., Климентьев А.Л.
Журнал: Вестник Витебского государственного технологического университета @vestnik-vstu
Рубрика: Технология и оборудование легкой промышленности и машиностроения
Статья в выпуске: 1 (32), 2017 года.
Бесплатный доступ
Предложен новый метод расчета кинетики сушки натуральных кож. Изложены результаты исследования сушки натуральной кожи методом регулярного режима нагревания влажных тел на основе комплексных обобщенных переменных. Представлена обработка экспериментальных данных по определению коэффициента сушки, позволяющая определять длительность сушки. Получены уравнения для определения основных параметров кинетики сушки натуральной кожи различных видов. Проведена проверка достоверности полученных формул и сопоставление экспериментальных значений параметров с расчетными по формулам.
Влагосодержание, среднеинтегральная температура, регулярный режим, критерий био, темп нагрева тела, темп убыли влагосодержания
Короткий адрес: https://sciup.org/142184999
IDR: 142184999 | УДК: 675.026.267
Текст научной статьи Исследование сушки натуральной кожи методом регулярного режима и обобщенными комплексными переменными
Сушка является не только теплофизическим, но и важным технологическим процессом, при котором материалы приобретают необходимые свойства. Правильно организованный процесс сушки должен не ухудшать технологические свойства высушиваемого материала, но заметно их улучшать. Технологические операции, которым подвергаются шкуры, прежде чем превращаются в натуральную кожу, очень сложны, разнообразны и многочисленны. Одной из последних технологических операций является дубление, в процессе которой кожа приобретает необходимые технологические свойства, при этом резко изменяются теплофизические и механические свойства по отношению к свойствам первоначального материала [1, 2].
Выбор режима сушки зависит от условий проведения процесса, в первую очередь температуры, влажности материала, скорости движения теплоносителя, способа сушки. Рациональный режим сушки должен обеспечивать высокие технологические свойства обрабатываемого материала при минимальной продолжительности сушки и создавать условия для проектирования сушильной установки с минимальными размерами [2, 3, 4].
ЦЕЛЬ ИССЛЕДОВАНИЯ
Расчет основных параметров кинетики сушки заключается в определении длительности процесса, температуры материала, плотности тепловых потоков, расхода тепла на сушку, интенсивности влагообмена, количества испаренной влаги. Все необходимые кинетические зависимости могут быть получены из аналитических решений системы уравнений тепломассопере-носа [1–5].
Однако поставленная задача получается такой, что получить точное решение невозможно, поскольку коэффициенты переноса тепла и влаги в материале изменяются в процессе сушки по сложным закономерностям в зависимости от температуры и влагосодержания [1, 4]. Поэтому для расчета кинетики сушки и определения основных параметров для выбора способа сушки, типа сушильного аппарата необходимы экспериментальные исследования, позволяющие разработать приближенные, достаточно надежные и простые экспериментальные уравнения с минимальным количеством постоянных [1]. При этом более универсальными являются такие методы обработки опытных данных, которые основаны на общих закономерностях сушки и устойчивых обобщенных комплексных переменных, что сближает теорию с практикой сушки и значительно сокращает объем расчетной работы при обработке эксперимента [4, 5].
Основной трудностью при описании кинетики сушки является невозможность согласования лабораторных условий сушки с условиями сушки в промышленной сушилке и соответствия кривых сушки переменному режиму работы сушильного аппарата [3, 4].
Наиболее обоснованное решение по масштабному переходу состоит в том, что при проведении экспериментальных исследований кинетики сушки в лабораторных условиях при постоянных режимах систематизировать все режимы сушки по температурам, относительной влажности воздуха и скорости движения теплоносителя, что позволяет исследовать влияние отдельных параметров на длительность процесса сушки [1–5].
Для построения кривой сушки при переменном режиме необходимо знать изменение температуры и влагосодержания материала в процессе сушки. Но в практике сушки режим изменяется прерывисто через отдельные промежутки времени. Следовательно, рассматривая кривые сушки для малых промежутков времени, для которых режим сушки постоянный и для которых вычисляется влагосодержание можно построить приближенную кривую сушки при переменном режиме [3].
Перенос результатов исследований из лабораторных условий на промышленные установки проводится с использованием теплового и материального баланса с проведением полупроиз-водственных экспериментов при переменном режиме сушки [1–5].
Правильно установленный рациональный режим сушки для конкретного материала позволяет определить минимальную длительность процесса, провести выбор конструкции и размеров сушильной камеры с минимальными энергозатратами на сушку [3–5].
СУШКА ТОНКИХ МАТЕРИАЛОВ
При сушке тонких материалов кривую кинетики сушки можно разделить на три участка: стадию прогрева материала, период постоянной скорости сушки (первый период), период убывающей скорости (второй период).
В стадии прогрева влажного тела подводимое к телу тепло расходуется на прогревание материала от начальной температуры tH до температуры tMT мокрого термометра, равной температуре tn поверхности материала ( tMT ~ tn ). Для тонких материалов период прогрева значительно меньше по сравнению с другими периодами сушки. Скорость сушки в стадии прогрева возрастает от нуля до скорости сушки в первом периоде N .
Из теплового баланса влажного тела следует, что тепло, подводимое к телу в стадии прогрева, идет на нагрев тела и жидкости, и можно записать Q > Q HCn [5]. При достижении температуры влажного материала равной tMT, стадия прогревания тела заканчивается и все подводимое тепло идет на испарение влаги из материала и выполняется равенство Q = Q HCn (приток тепла равен его расходу). Наступает первый период сушки, в котором температура равна tMT = tn и сохраняется постоянной до начала второго периода сушки.
С уменьшением влагосодержания ниже кри- тического иКР температура влажного материала непрерывно возрастает, а теплота на испарение влаги из материала QHCn постоянно убывает (второй период сушки).
Использованный первичный материал, необходимый для обработки данных комплексными переменными в виде кривых сушки и температурных кривых, приведен в монографии А. В. Лыкова [2] в виде протоколов наблюдений с указанием номера опыта и вида кожи.
На рисунке 1 изображены кривые сушки и = f( т ) и температурные кривые t = f(u) для процесса конвективной сушки краснодубной юфти при различных режимах. Наблюдаются стадия прогрева материала, период постоянной скорости сушки с периодом постоянной температурой на уровне tMT и второй период с непрерывным увеличением температуры до tC при т ^ да .
Для тонких материалов с периодом постоянной температуры в первом периоде при мягких режимах сушки градиентом температуры по сечению влажного тела можно пренебречь [4]. В [4, 5] стадию прогрева материала предлагается аппроксимировать уравнением где du / dT — скорость сушки; N — скорость сушки в первом периоде; t — среднеинтегральная температура материала.
Время нагрева материала от tH до tMT определяется интегрированием уравнения (1)
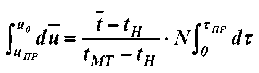
.
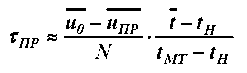
.
В качестве примера по уравнению (2) определим время прогрева для процесса сушки красно-дубной юфти при режиме tC = 50 oC ; скорости воздуха v = 0,5 м/с ; относительной влажности Ф = 45 % (рисунок 1, кривая (2)).
Эксперимент: U0 = 0,97 ; tH = 20 oC; ипр = 0,80; tMT = tn = 35 oC; N = 0,0070 мин1; t = 34,5 oC; т пркс = 25 мин.
По формуле (2)
0,97-0,80
np 0,0070
35-20
мин.
34,5-20
du dT
^мт~ hi
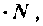
Сопоставление значения т пр материала с экспериментом показывает хорошее совпадение значений и, следовательно, пренебрежение гра-

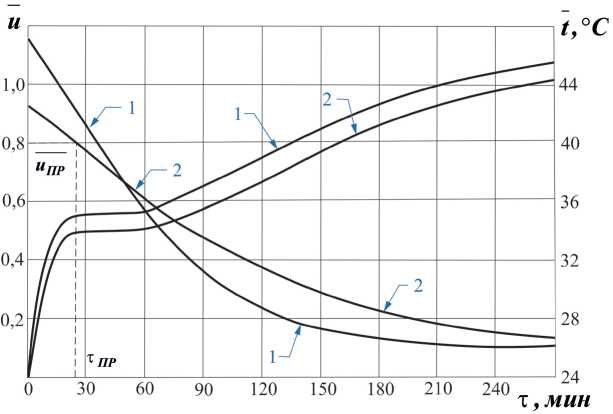
Рисунок 1 — Кривые сушки и = f( т ) и температурные кривые t = f(u) в процессе сушки краснодубной юфти при режимах: 1 — tC = 50 oC ; v = 1 м/с ; ф = 45 % ; 2 — tC = 50 oC ; v = 0,5 м/с ; ф = 45 %
диентом температуры по сечению влажного тела не вносит в расчеты значительной погрешности. ОСНОВЫ ТЕОРИИ РЕГУЛЯРНОГО РЕЖИМА
Рассмотрим основные положения регулярного режима, которые необходимы в расчетах кинетики сушки тонких материалов. При сушке тонких плоских влажных материалов теплообменный критерий Био Bi < 1 и при отсутствии во влажном теле термического переноса вещества, когда градиентом температуры по сечению тела можно пренебречь и приближенно допустить tMT ~ t n ,то относительную температуру материала можно определять по формуле [6, 7]
, (3)
*мт где F0 — критерий Фурье.
Из теории регулярного режима нагревания твердых тел при равномерном начальном распределении температуры в теле при Bi < 0,1 (практически достаточно Bi < 0,4) следует, что темп нагрева твердого тела определяется выражением [6, 8]
а
, (4)
^О" Ро‘ ^v где mt — темп нагрева твердого тела; α — коэффициент теплообмена; c0 — теплоемкость сухого тела; ρ0 — плотность; Rν = V / F — отношение объема тела к поверхности.
Темп нагрева тела mt зависит от физических свойств тела, его геометрической формы, условий теплообмена на поверхности тела и не зависит от режима сушки [6–8]. Д л я безразмерного влагосодержания материала U можно записать выражение, вытекающее из решения дифференциального уравнения массопереноса [7], аналогичное зависимости (3)
——™ XX- XX- г> / * _ _ \
, (5)
U-Q Ир где Bim, Fom — массообменные критерии Био и Фурье; u0, u, uÐ — начальное, текущее и равновесное влагосодержание материала.
Комбинации критериев Bi·Fo и Bim·Fom представляют важные устойчивые обобщенные переменные, характерные для процесса сушки. Подставляя все значения теплофизических коэффициентов в критерии подобия в уравнения (4) и (5), получим
; (6)
, (7)
где τ II — время сушки во втором периоде; τ — время сушки, отсчитываемое от начала процесса; mu — темп убыли влагосодержания.
Темп нагрева материала и темп убыли влаго- содержания определяются экспериментально по зависимостям [6, 7]
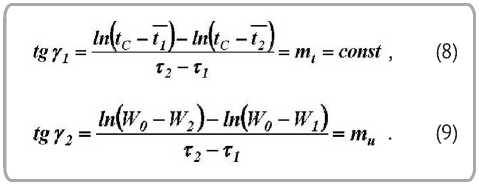
На рисунке 2 представлены кривые сушки для процессов сушки краснодубной юфти и стелечного полувала при различных режимах и начальных значениях влагосодержания [2].
На рисунке 1 и рисунке 3 даны кривые сушки и температурные кривые в процессах сушки юфти и опоека при различных режимах.
Темп убыли влагосодержания, определяемый формулой (9), находится в сложной функциональной зависимости от режима сушки, начального влагосодержания ( u0 ) и ряда других факторов, влияющих на процесс сушки [8]. В этих условиях отношение скорости сушки в периоде постоянной скорости N к начальному влагосо-держанию ( u0 ) является обобщенной переменной ( N / u0 ), учитывающей влияние режимных параметров на процесс сушки [8]. Обработкой большого числа экспериментальных по конвективной сушке различных материалов (более 17 наименований тонких материалов и различных видов натуральной кожи) установлена общая зависимость для темпа убыли влагосодержания
. (10)
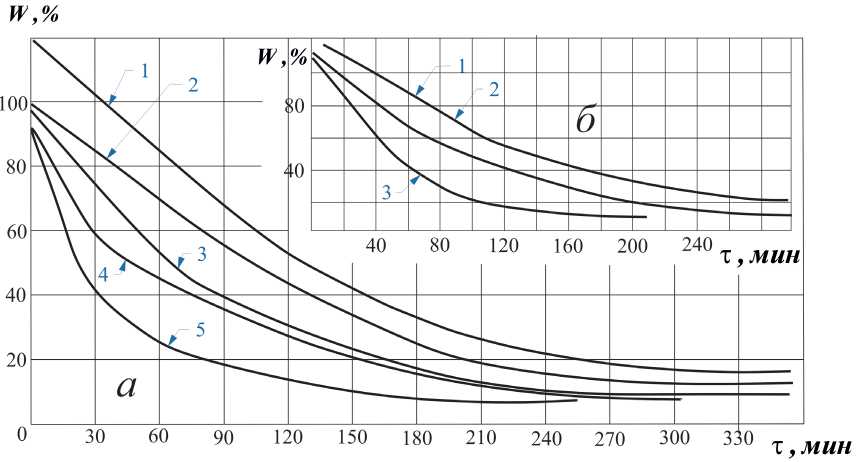
Рисунок 2 — Кривые сушки W = f( τ ) для процессов сушки краснодубной юфти (а) при режимах:
1 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 2 — tC = 50 oC ; ν = 0,5 ì/ñ ; φ = 40 % ; 3 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 40 % ; 4 — tC = 50 oC ; ν = 1 ì/ñ ; φ = 30 % ; 5 — tC = 60 oC ; ν = 3 ì/ñ ; φ = 30 % ; стелечного полувала (б) при режимах: 1 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 2 — tC = 60 oC ; ν = 1 ì/ñ ;
φ = 60 % ; 3 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 40 %
X)
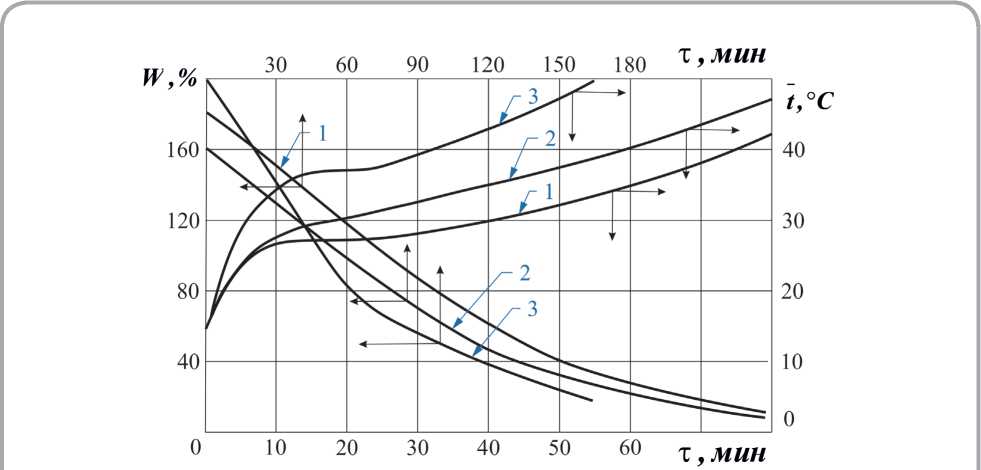
Рисунок 3 — Кривые сушки W = f( τ ) и температурные кривые t = f( τ ) для процессов сушки хромового опойка при режимах: 1 — tC = 45 oC ; ν = 1 ì/ñ ; φ = 27,5 % ; 2 — tC = 49 oC ; ν = 1,5 ì/ñ ; φ = 30 % ; 3 — переменный режим до WKP = 100 % tC = 60 oC ; φ = 50 % ; от WKP до W = 22 % tC = 45 oC ; φ = 30 % ; скорость воздуха ν = 0,5 ì/ñ
Обработкой опытных данных методом наименьших квадратов по конвективной сушке различных видов натуральной кожи при разных режимах сушки по уравнению (8) получена общая зависимость для всех видов кожи
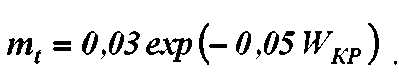
Уравнения (3) и (5) на основании (6), (7) [8]
запишем в виде:
|
® = |
tc-t *С - ^мт |
, |
(12) |
|
|
й= |
и -иР и0 - иР |
. |
(13) 1 |
Анализ опытных данных по конвективной сушке различных видов натуральной кожи показал, что регулярный режим по температурам наступает с началом второго периода от температуры t ^ T ~ tn и время сушки отсчитывается от τ II = 0 (рисунок 4 а ). Регулярный режим по влагосодержаниям (рисунок 4 б ) наступает сразу по окончании стадии прогрева материала от начальной температуры tÍ до tÌÒ и достижения èÏÐ . Видно (рисунок 4 б ), что вся группа прямых в координатах ln(WÏÐ - W) = f ( τ ) начи на ется от влагосодержания прогрева материала èÏÐ , а и время сушки τ необходимо отсчитывать от начала процесса влагосодержания è0 .
Из решения уравнений (12) и (13) определяются среднеинтегральная температура материала во втором периоде и длительность сушки до любого заданного влагосодержания материала
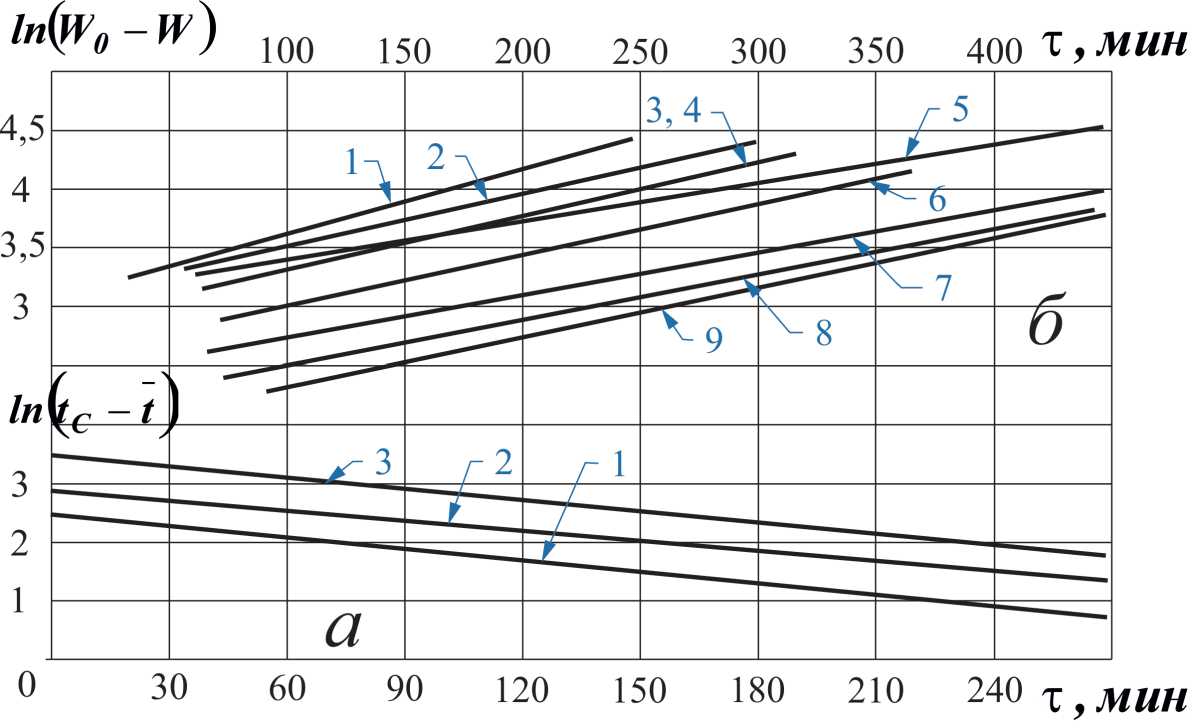
Рисунок 4 — Зависимость ln(tC - t) = f( τ ) (а) для процессов сушки краснодубной юфти при режимах:
1 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 2 — tC = 50 oC ; ν = 0,5 ì/ñ ; φ = 45 % ; 3 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 40 % ; зависимость ln(W0 - W) = f( τ ) (б) для процессов сушки краснодубной юфти при режимах: 1 — tC = 50 oC ; ν = 1 ì/ñ ; φ = 45 % ; 2 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 40 % ;
3 — tC = 50 oC ; ν = 1 ì/ñ ; φ = 30 % ; 4 — tC = 60 oC ; ν = 3 ì/ñ ; φ = 30 % ; 5 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 6 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 60 % и рантовой подошвы при режимах: 7 — tC = 40 oC ;
ν = 1 ì/ñ ; φ = 50 % ; 8 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 45 % ; 9 — tC = 50 oC ; ν = 0,5 ì/ñ ; φ = 50 %
______________________________________________________7

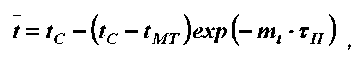
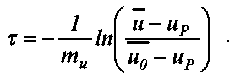
Тепловой поток на нагрев влажного тела во втором периоде сушки равен [4, 5]
du = с^ ® , , (16)
F ат
Подставляя (19) в (20) с учетом (4) получим t-tc Мс <мЛ^Р^ mt"xii^ . (21)
Вывод уравнения (21) совпадает с выводом уравнения (14), что подтверждает справедливость зависимостей (3) и (4) для тонких материалов при значениях критерия Био Bi < 1.
Если подставить (20) в зависимость (1), то получим приближенное уравнение кривой кинетики сушки с учетом стадии прогрева материала [5]
где cW — теплоемкость влажного материала; G0 и F — масса сухого материала и его поверхность; dt / d τ — скорость изменения температуры влажного тела во втором периоде сушки.
В случае конвективной сушки приток тепла и = и0
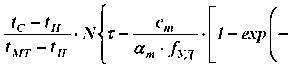
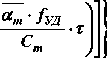
на нагрев влажного тела определяется уравнением теплообмена [1–4]
Чп = ® кс - И . (17)
Тогда для конвективной сушки можно записать
“•fv^C-tV C1V^- , (18)
уДх ’ w dr где fÓÄ = F/ G0 — удельная поверхность влажного материала.
Удельная поверхность материала выражается зависимостью
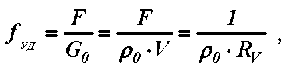
где ρ0 — плотность сухого тела; V — объем тела; RV = V / F — характерный размер тела равный для плоского материала его толщине RV = δ .
Решен и ем уравнения (18) при начальном условии t(0) = tMT (начало второго периода сушки) получим уравнение температурной кривой в периоде падающей скорости [5]
где cm — удельная массоемкость влажного тела; αm — коэффициент массообмена.
После преобразований с учетом (7) и (19) по лучим
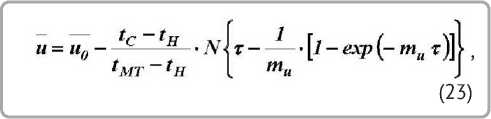
Уравнение (23) получено из условия, когда равновесное влагосодержание материала uP = 0 . При сушке тонких материалов при температурах tÑ ≈ 30–60 °C и высоких относительных вла-госодержаниях воздуха φ в сушильной камере φ ≈ 45–80 % необходимо учитывать равновесное влагосодержание материала uÐ .
При конвективной сушке натуральной кожи при температурах tÑ = 40–60 °C и φ ≈ 45–80 % равновесное влагосодержание кожи uÐ ≈ 0,12– 0,2.
С учетом равновесного влагосодержания uÐ уравнение (23) примет вид
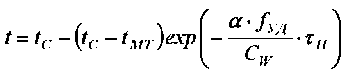
В качестве примера приведем расчет кривой сушки по уравнению (24) для процессов сушки краснодубной юфти и рантовой подошвы.
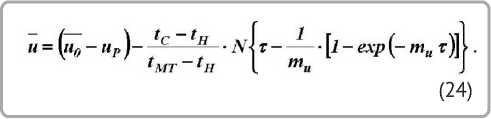
Из приведенных расчетов видно, что расчетная кривая сушки по уравнению (24) при значениях влагосодержания близких к равновесным не просчитывается.
Анализ большого числа экспериментальных данных по сушке различных материалов разными способами энергоподвода показал, что кривые сушки во втором периоде представляют собой две, а для натуральной кожи три сопряженных экспоненты [1–4], и описать кривую сушки одной экспоненциальной зависимостью можно только приближенно.
Во-вторых, при влагосодержаниях натуральной кожи близких к 20 % и ниже (зона углубления испарения внутрь материала) значительная часть тепла идет на нарушение связи влаги с материалом и теплота парообразования не соответствует действительной [1, 3]. На рисунке 5 б представлена кривая интенсивности (скорости сушки) испарения для процесса сушки красно-дубной юфти при режиме tÑ = 50 °C , скорости воздуха ν = 1,5 ì/ñ , относительной влажности воздуха φ = 30 % ( W0 = 160 %, WКР1 = 80 %, WКР2 = 46 %, WКР3 ≈ 24 %, WÐ = 12 %). Видно, что кривая скорости сушки представляет собой три участка прямых сопряженных в точках WКР1 , w , W „
КР2 , КР3 .
На рисунке 5 а представлена обобщенная кривая сушки для различных видов натуральной кожи при разных режимах сушки. Видно, что с допустимой погрешностью обработки опытных данных, все точки укладываются на одну прямую. Регулярный режим по влагосодержаниям наступает после окончания стадии прогрева влажного материала.
Б.С. Сажиным [4, 5] применительно для конвективной сушки тонких влажных материалов разработан метод расчета кинетики сушки на основе единого обобщенного уравнения массо-передачи, позволяющего описывать весь процесс сушки, включая стадию прогрева материала, первый и второй периоды сушки. При таком подходе коэффициент сушки K для каждого режима остается постоянной величиной при фиксированных условиях проведения процесса сушки [5]. При этом исключается графическое дифференцирование при построении кривой скорости сушки, связанное с погрешностью [5].
Уравнение массопередачи применительно к конвективной сушке представляется в виде [5]
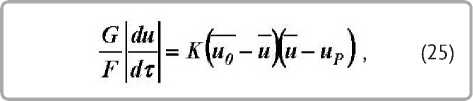
где G / F — общая масса влажного материала, приходящая на единицу поверхности испаре-
Таблица 1 — Результаты расчета кривой сушки для краснодубной юфти
|
u |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
|
τ ЭКСmin |
27 |
38 |
45 |
58 |
69 |
90 |
115 |
142 |
|
u ÐÀÑ× |
0,93 |
0,84 |
0,72 |
0,63 |
0,48 |
0,36 |
– |
— |
Примечание. Режим сушки и данные эксперимента: tc = 50 °C ; v = 1 м/с ; ф = 45 %; и0 = 1,13; иК Р = 0,67; ир = 0,135; tÍ = 20 °C ; tÌÒ = 35 °C ; mu = 8,5 · 10–3 ìèí–1 ; N = 9,45 · 10–3 ìèí .
Таблица 2 — Результаты расчета кривой сушки для рантовой подошвы
|
u |
0,65 |
0,5 |
0,4 |
0,35 |
0,25 |
0,2 |
0,3 |
0,2 |
|
τ ЭКСmin |
82 |
152 |
220 |
247 |
400 |
498 |
115 |
142 |
|
u ÐÀÑ× |
0,68 |
0,47 |
0,41 |
0,37 |
– |
– |
– |
– |
Примечание. Режим сушки и данные эксперимента: tc = 50 °C ; v = 0,5 м/с ; ф = 50 %; и0 = 0,87; иК Р = 0,62; ир = 0,105; tÍ = 20 °C ; tÌÒ = 34 °C ; mu = 4,45 · 10–3 ìèí–1 ; N = 2,0 · 10–3 ìèí .
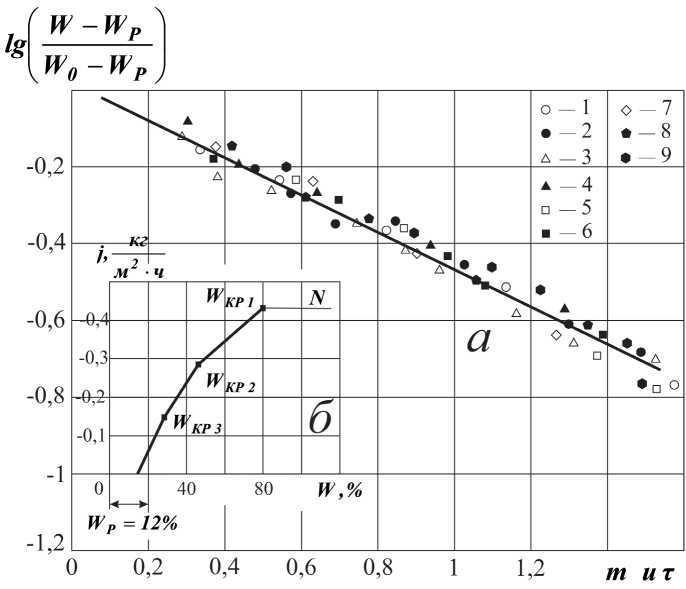
Рисунок 5 — Зависимость относительного влагосодержания lg(W / Wo) от относительного времени сушки m и τ (а) (режимы сушки для рисунка 5 а указаны на рисунке 4) и кривая интенсивности сушки краснодубной юфти (б) при режиме: tC = 50 oC ; ν = 1,5 ì/ñ ; φ = 30 %
ния; K — коэффициент сушки.
Отношение G / F представим в виде соот-
Принимая во внимание, что GÂË / G0 = è 0 получим

где GÂË и G0 — масса влаги в материале и масса по опытным кривым сушки (рисунок 1). Если в сухого тела. системе координат Z = f( τ ) построить кривые
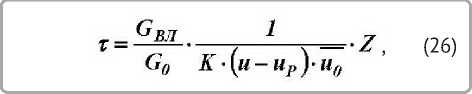
Интегрированием уравнения (25) от влагосо- сушки, то в такой системе координат образуются держания в стадии прогрева материала èÏÐ до прямые для каждого режима сушки [5]. Причем текущего è при начальном è0 получим [5] угол наклона этих прямых определяет коэффи циент сушки K, а отрезки, отсекаемые на оси Z, устанавливают величину Z0 = uÏÐ [5].
На рисунке 6 представлены зависимости Z = f(τ) для процессов конвективной сушки различных видов натуральной кожи при разных где Z равно [5]
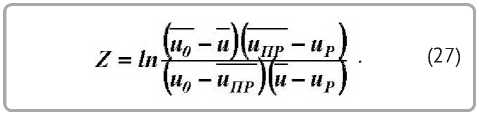
режимах сушки.
В практике сушки коэффициент сушки K определяется также опытным путем построением кривой сушки в координатах ln(W - WP) = = f( τ ) .
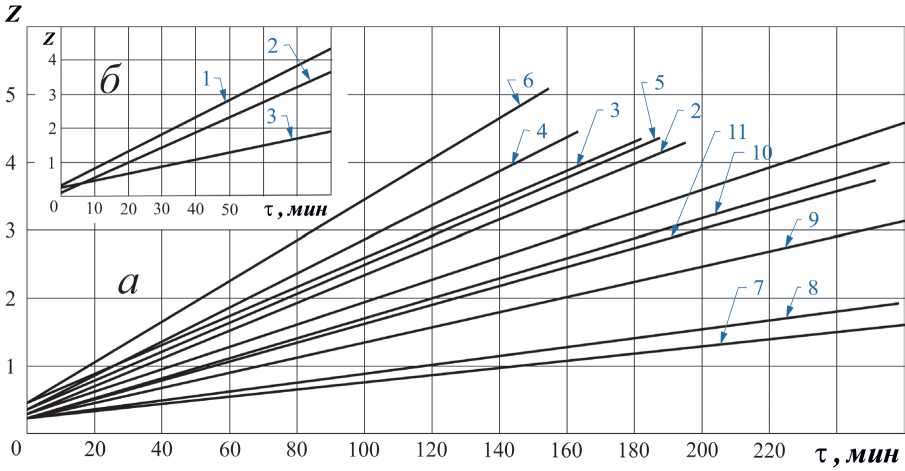
Рисунок 6 — Зависимость параметра Z от длительности сушки для различных видов натуральных кож: а) юфть, режимы сушки: 1 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 2 — tC = 50 oC ; ν = 0,5 ì/ñ ; φ = 45 % ; 3 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 40 % ; 4 — tC = 50 oC ; ν = 1 ì/ñ ; φ = 45 % ; 5 — tC = 50 oC ; ν = 1,5 ì/ñ ; φ = 30 % ; 6 — tC = 60 oC ; ν = 3 ì/ñ ; φ = 30 % ; рантовая подошва, режимы сушки: 7 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 50 % ; 8 — tC = 50 oC ; ν = 0,5 ì/ñ ; φ = 50 % ; 9 — tC = 60 oC ; ν = 0,5 ì/ñ ; φ = 45 % ; стелечный полувал, режимы сушки: 10 — tC = 40 oC ; ν = 1 ì/ñ ; φ = 60 % ; 11 — tC = 60 oC ; ν = 1 ì/ñ ; φ = 60 % ; б) хро мо вый опоек, режимы сушки: 1 — tC = 45 oC ; ν = 1 ì/ñ ; Ф = 27,5 % ; 2 — режим сушки переменный до иКР = 1 tC = 60 o C ; v = 0,5 м/с ; ф = 50 % ; при и < иКР (второй период сушки) tC = 45 oC ; ν = 0,5 ì/ñ ; φ = 30 %
Сравнение значений коэффициента сушки K , определенные этими двумя различными методами, показало вполне удовлетворительное совпадение значений K в пределах погрешности проведения эксперимента.
Так, например, при сушке краснодубной юфти в режиме tC = 50 oC ; ν = 1 ì/ñ ; φ = 45 % определенные по зависимости Z = f( τ ) (рисунок 6, прямая 4) значение коэффициента сушки составляет K = 0,016 ìèí–1 , а значение определенное по зависимости ln(W - WP) = f( τ ) K = 0,0145 ìèí–1 . Совпадение значений K вполне удовлетворительное.
ЗАКЛЮЧЕНИЕ
На основе регулярного теплового режима нагрева тонких тел получены основные характеристики для расчета кинетики сушки натуральной кожи. Установлены обобщенные зависимости для определения темпа нагрева и темпа убыли влагосодержания. Получены экспериментальные уравнения для расчета длительности процесса сушки для различных видов натуральной кожи. Получены уравнения для расчета коэффициента сушки и длительности процесса из условия рассмотрения сушки как единого процесса, включая период прогрева материала и периоды постоянной и падающей скорости сушки. Дано сопоставление численных значений параметров сушки с экспериментальными. Проведена проверка достоверности полученных уравнений.
Список литературы Исследование сушки натуральной кожи методом регулярного режима и обобщенными комплексными переменными
- Лыков, А.В. (1968), Теория сушки, Москва, Энергия, 590 с.
- Лыков, А.В. (1938), Кинетика и динамика процессов сушки и увлажнения, Москва, Гизлегпром, 776 с.
- Рудобашта, С.П. (2010), Теплотехника, Москва, Колосс, 599 с.
- Акулич, П.В. (2010), Расчеты сушильных и теплообменных установок, Минск, Беларуская навука, 443 с.
- Сажин, Б.С. (1984), Основы техники сушки, Москва, Химия, 320 с.
- Лыков, А.В. (1967), Теория теплопроводности, Москва, Высшая школа, 600 с.
- Лыков, А.В., Михайлов, Ю.А. (1963), Теория тепломассопереноса, Москва -Ленинград, Госэнергоиздат, 535 с.
- Ольшанский, А.И. (2014), Регулярный тепловой режим нагревания влажных плоских капилляропористых материалов в процессе их сушки, Инженерно -физический журнал, 2014, Т. 87, № 6, С. 1308-1318.


