Исследование связи согласующей цепи с входными резонаторами каналов в микрополосковом диплексере

Цитирование: Афонин, А.О. Исследование связи согласующей цепи c входными резонаторами каналов в микрополосковом диплексере / А.О. Афонин, А.А. Лексиков, А.А. Лексиков, И.В. Говорун, А.М. Сержантов, А.В. Угрюмов // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(7). С. 871–881. DOI: 10.17516/1999-494X-0272

один конец которого общий порт, а второй разомкнут. Этот отрезок связан электромагнитно с входными резонаторами каналов [8, 9]. Очевидно, что такое решение перспективно с точки зрения миниатюризации устройства. Наиболее эффективным способом уменьшения микро-полосковых устройств признано применение в них подложек с высоким значением относительной диэлектрической проницаемости. В этой статье мы рассматриваем микрополосковый диплексер на подложке с ε = 80, в котором в качестве согласующей цепи (СЦ) используется простой отрезок микрополосковой линии (МПЛ), и приводим результаты исследования влияния параметров СЦ на коэффициенты связи между СЦ и входными резонаторами каналов. Подобные данные неоценимы при разработке диплексеров. Результаты проведенных исследований показали, что вопреки ожиданиям можно разрабатывать микрополосковые диплексеры с простейшей СЦ на подложках с высоким значением ε и относительной полосой пропускания каналов 10 % и более (ε ˃˃ 10).

1.    Топология исследуемого диплексера

На рис. 1 приведена топология исследуемого диплексера и приведены его структурные параметры, а на рис. 2 показана его амплитудно-частотная характеристика (АЧХ), полученная по результатам моделирования при следующих параметрах структуры: подложка с ε = 80 и толщиной h_d = 2 мм, ее поперечные размеры 16 мм×25.5 мм. Низкочастотный канал: длина полосковых проводников резонаторов l ₁ = 17.25 мм, l ₂ = 16.0 мм, их ширина w = 1 мм, зазор между проводниками S ₁ = 2.7 мм. Высокочастотный канал: длина полосковых проводников резонаторов l ₃ = 13.0 мм, l ₄ = 12.8 мм, зазор между ними S ₂ = 3.7 мм. СЦ – полосковый проводник согласующей цепи, его длина 15.0 мм и ширина 0.2 мм. Зазор между согласующим проводником и входным резонатором низкочастотного канала равен s_{p 1} = 0.7 мм, между входным резонатором высокочастотного канала – s_{p 2} = 0.4 мм; длина области перекрытия СЦ и входных

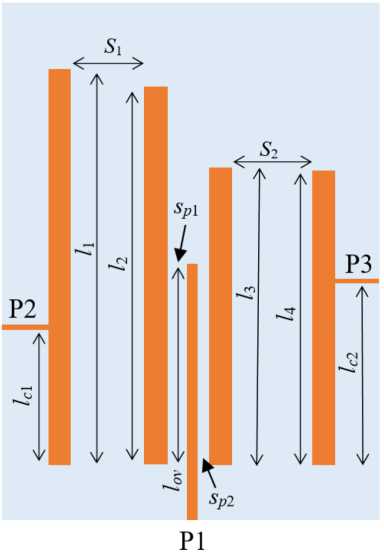
Рис. 1. Топология диплексера с обозначением структурных параметров

Fig. 1. The diplexer layout and its structural parameters

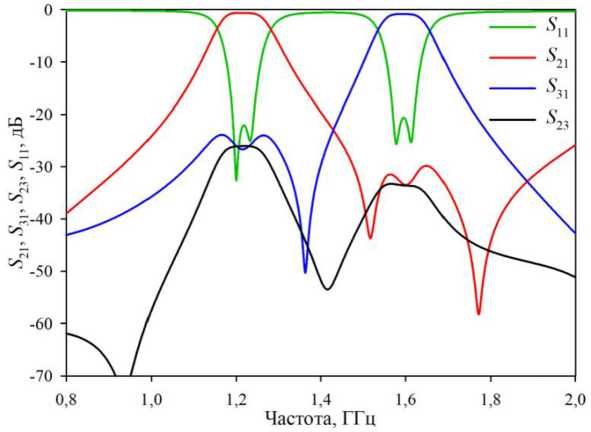
Рис. 2. АЧХ диплексера, полученная в результате моделирования

Fig. 2. Simulated frequency responses of the proposed diplexer резонаторов lov = 8.5 мм. Полосковые проводники, подключающие порты P2 и P3, имеют размеры 2.0 × 0.2 мм. Точка подключения порта P2 локализована на расстоянии lс1 = 5.8 мм от нижнего конца резонатора в НЧ-канале. Точка подключения порта P3 локализована на расстоянии lс2 = 4.55 мм от верхнего конца резонатора в ВЧ-канале. Все резонаторы выровнены по нижнему концу.

Из данных рис. 2 могут быть получены следующие параметры АЧХ: центральные частоты каналов 1218 МГц и 1596 МГц, а их относительные ширины полос пропускания 10.4 % и 7.6 % для НЧ- и ВЧ-каналов соответственно.

2.    Методика исследования

Хотя примененная согласующая цепь очень проста, тем не менее крайне полезно с точки зрения проектирования знать, как ее параметры влияют на взаимодействие с входными резонаторами каналов. С этой целью мы исследовали коэффициенты связи СЦ с входными резонаторами каналов в зависимости от ее параметров, отдельно в субструктуре «входной резонатор НЧ-канала – СЦ» и субструктуре «СЦ – входной резонатор ВЧ-канала». В результате получены зависимости коэффициента связи k c входными резонаторами каналов от длины и ширины проводника СЦ. Также изучено влияние длины области перекрытия (СЦ и входного резонатора) l_ov на коэффициент k .

Исследования проводили теоретически с использованием понятия частотно-зависимых коэффициентов связи пары взаимодействующих резонаторов, которые рассчитывали на основе энергетического подхода, описанного ранее в работах [10, 11]. В этом методе рассчитывают электромагнитные энергии, запасаемые резонаторами совместно и по отдельности, и затем из них вычисляют коэффициенты связи. Электромагнитные энергии рассчитывают с использованием распределения амплитуд высокочастотных токов и напряжений по длине проводников, которые в свою очередь определяют из системы линейных уравнений, получаемых из уравне-– 874 – ний волны (1) при условиях сохранения заряда и непрерывности напряжения на концах проводников всех регулярных отрезков.

На рис. 3 и 4 приведены схематические изображения субструктур «входной резонатор НЧ-канала – СЦ» и «СЦ – входной резонатор ВЧ-канала» соответственно, а также их одномерные модели.

Для построения 1-D-модели микрополосковая субструктура разбивается на отрезки многосвязанных и одиночных линий, как это показано штрихованными линиями на рис. 3 и 4. И, таким образом, НЧ-субструктура состоит из двух одиночных линий и двух двухсвязанных линий. То же самое можно сказать и о ВЧ-субструктуре. Отрезки линий соединены последовательно. В модели учтены концевые емкости разомкнутых концов отрезков.

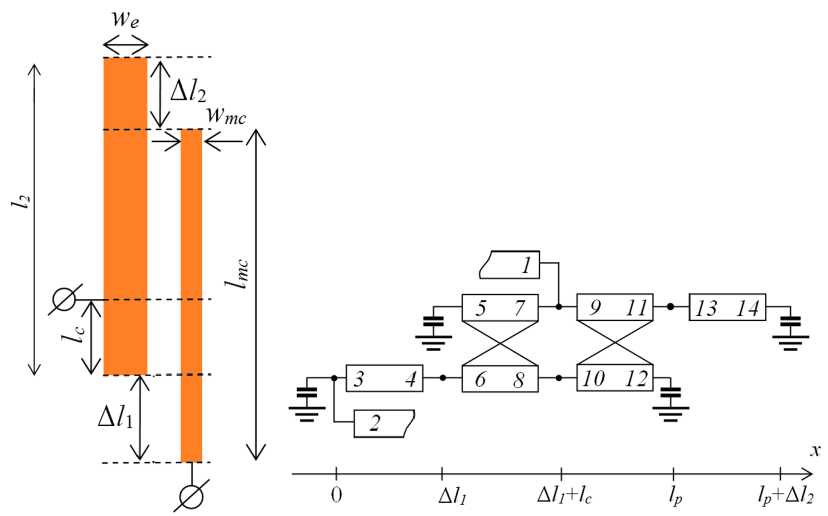
Рис. 3. Топология субструктуры «входной резонатор НЧ-канала – СЦ» и ее одномерная модель

Fig. 3. Substructure «Low-frequency channel’s input resonator – matching circuit» and its 1-D model

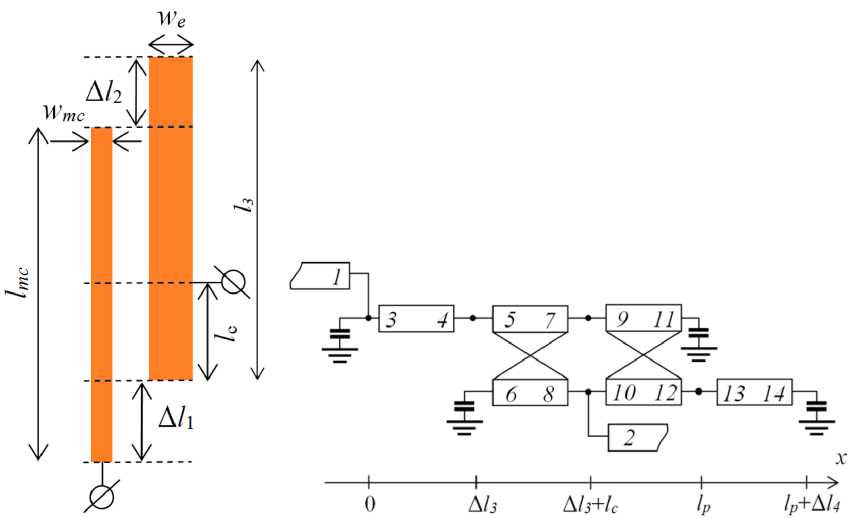
Рис. 4. Топология субструктуры «СЦ – входной резонатор НЧ-канала» и ее одномерная модель

Fig. 4. Substructure «Matching circuit – high-frequency channel’s input resonator» and its 1-D model

Для этих моделей из решения волнового уравнения (1) при условии сохранения заряда и непрерывности напряжения на концах всех отрезков проводников были получены две системы линейных уравнений. Эти системы, связывающие амплитуды проходящих и отраженных волн с амплитудой падающей волны, позволяют вычислить амплитудно-частотные характеристики, а также распределения токов и напряжений в проводниках. В вычислениях рассматривали только волны основного типа, а параметры одиночных и связанных линий рассчитывали на основе квази-TEM приближения.

Токи I i и напряжения U i в i -м проводнике сегмента связанных микрополосковых линий (МПЛ) искали в форме решения волнового уравнения:

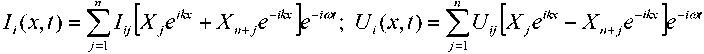
где x - координата; t - время; ю - частота; n - номер полоскового проводника в сегменте связанных линий; Xj - относительная амплитуда j -й нормальной волны; I j , U y - амплитуды тока и напряжения j -й нормальной волны в i -м проводнике.

На рис. 3 и 4 прямоугольниками обозначены полосковые проводники в сегменте связанных и одиночных отрезков МПЛ. Кресты в форме «Х» обозначают связи. Патчи 1 и 2 на схеме означают входную и выходную линии передачи. Для каждой секции связанных МПЛ введено собственное начало координаты x , которое помещается на левом краю секции. Это означает, что амплитуды всех нормальных волн X ij устанавливаются на левом краю секций, а на правом краю они будут иметь соответствующие набеги фазы. Для определенности считается, что положительное направление тока совпадает с направлением оси x .

Числами в прямоугольниках задана непрерывная нумерация нормальных волн во всех сегментах связанных МПЛ. Числа, расположенные в левой части прямоугольников, – номера нормальных волн, распространяющихся в положительном направлении x , а справа - номера волн, распространяющихся в противоположном направлении. Отметим, что хотя номер каждой из волн фигурирует только в одном из прямоугольников, волны с таким номером распространяются во всех n связанных проводниках одновременно. Амплитуды X j всех пронумерованных волн (j' = 1,...,12) считаются неопределенными и должны быть найдены в результате вычислений. Амплитуда падающей волны считается заданной. Система линейных алгебраических уравнений для нахождения всех пронумерованных амплитуд нормальных волн была найдена из выражения (1) и условий равенства сумм входящих сумме выходящих токов в точках соединения проводников, а также равенства напряжений в каждой паре проводников с разных сторон от точки их соединения. Полное число уравнений для всех точек соединений равно числу искомых амплитуд нормальных волн. Решение системы дает амплитуды волн, отраженных от всех портов устройства, когда волна заданной амплитуды падает на один из портов, а на всех остальных портах падающие волны отсутствуют. Более того, система позволяет определить амплитуду любой волны в любом регулярном сегменте МПЛ, а использование этих амплитуд – вычислить ток и напряжение в любой точке любого проводника.

В качестве примера рассмотрим уравнения, соответствующие соединению 1-7-9, (рис. 3). Здесь 1 – это входной фидер, имеющий импеданс 50 Ом. Уравнение для токов

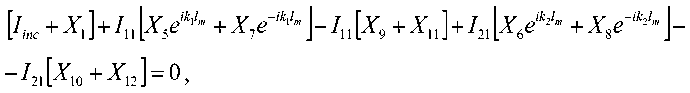
где k j – электрическая длина сегмента l m (на частоте j -й волны).

Первое уравнение для напряжений получается из равенства напряжений в проводниках (i = 1) левого и правого сегментов МПЛ, соединенных в точке 1-7-9 (рис. 3):

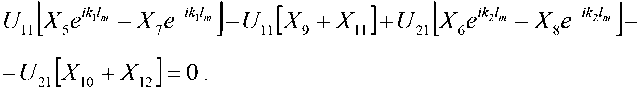
Уравнение для напряжений получается из равенства напряжений на входной линии и сегменте МПЛ, находящемся справа от точки 1-7-9 (рис. 3):

После записи всех уравнений для всех точек соединения в сегментах связанных МПЛ в рассматриваемой секции полученную систему линейных уравнений с комплексными коэффициентами решаем численным методом Гаусса.

Таким образом мы находим 12 неизвестных амплитуд X_i . Аналогичным способом находим и решаем уравнения для ВЧ-канала.

Для нахождения частотно-зависимых коэффициентов связи, как сказано выше, использовали энергетический подход [10, 11]. Он был разработан для расчета частотно-зависимых коэффициентов связи микрополосковых резонаторов (МПР) и постулирует коэффициент связи как отношение электромагнитной энергии, запасенной резонаторами совместно к полной энергии, запасенной резонаторами по отдельности. Поскольку распределение амплитуд СВЧ-токов и напряжений вдоль МПР зависит от частоты, их взаимодействие и коэффициенты связи тоже частотно-зависимы. Очевидно, что нет каких-либо физических причин, ограничивающих этот подход только резонаторами с одинаковыми резонансными частотами. Поэтому мы использовали его для определения коэффициентов связи согласующей цепи диплексера с входными резонаторами каналов диплексера.

Запишем выражения для энергий, запасаемых субструктурой НЧ-канала, используя токи, напряжения и погонные параметры L и C – погонные емкость и индуктивность. Они получатся интегрированием плотностей энергии по соответствующим отрезкам проводников. Магнит -ные и электрические энергии, запасаемые резонатором и проводником СЦ раздельно:

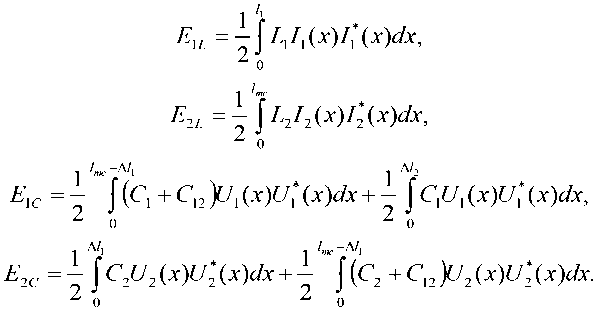
Магнитные и электрические энергии, запасаемые резонатором и проводником СЦ совместно:

Д₂£=1т ^LJ^I^xW, о

^тс ^— ^1

E_12C=Im C^J^x^U^x^dx.

о

Здесь звездочка (*) означает операцию комплексного сопряжения.

L1, L2, C1, C2, L12, C12 — погонные индуктивности и емкости проводников резонатора и СЦ и их погонные взаимные индуктивность и емкость.

Окончательно частотно-зависимые коэффициенты индуктивной, емкостной и полной свя- зи согласующей цепи с входным резонатором НЧ-канала выражаются [11]

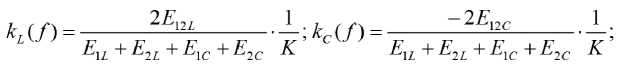
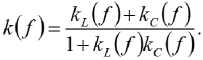
Здесь K – модуль коэффициента передачи по напряжению субструктуры НЧ-канала.

3.    Исследование связи согласующей цепи с входными резонаторами каналов

На основе вышеприведенных математических выражений была написана компьютерная программа для расчета частотно-зависимых коэффициентов связи к между СЦ и входными резонаторами каналов. Из этих зависимостей извлекали значения к , соответствующие центральным частотам каналов. Подобные зависимости рассчитывали для субструктур при вариации параметров СЦ. Такими параметрами являются: l mc - длина проводника СЦ, w mc - ширина проводника СЦ и l ov – длина области перекрытия проводника СЦ и резонатора.

На рис. 5 приведены рассчитанные частотные зависимости коэффициента связи к , соответствующие субструктурам с параметрами топологии, как в диплексере на рис. 1. Зависимости имеют максимумы, соответствующие центральным частотам каналов. Значения в этих максимумах и исследовали в зависимости от параметров согласующей цепи.

На рис. 6 изображены зависимости коэффициента связи согласующей цепи с входными резонаторами каналов от длины l mc (а) и ширины w mc (б) согласующего проводника.

Поведение коэффициента связи от длины l_mc для разных каналов отличается. Так, для ВЧ-канала кривая к(l mc ) имеет максимум в районе l mc = 12^13 мм, в то время как связь для НЧ-канала усиливается с увеличением длины СЦ. Используя эти зависимости можно подобрать такую длину согласующей цепи, которая обеспечит необходимую величину связи и для низкочастотного, и для высокочастотного каналов. Поведение зависимостей k от ширины СЦ для обоих каналов схоже: здесь коэффициенты связи имеют максимумы при близких значениях ширины проводника СЦ w mc = 0.1…0.2 мм. Увеличение w mc приводит к уменьшению величины связи. Характер кривых к ( w mc ) объясняется тем, что при росте ширины проводника СЦ уменьшается плотность тока, который в нем протекает, что и уменьшает величину взаимодействия с входными резонаторами каналов.

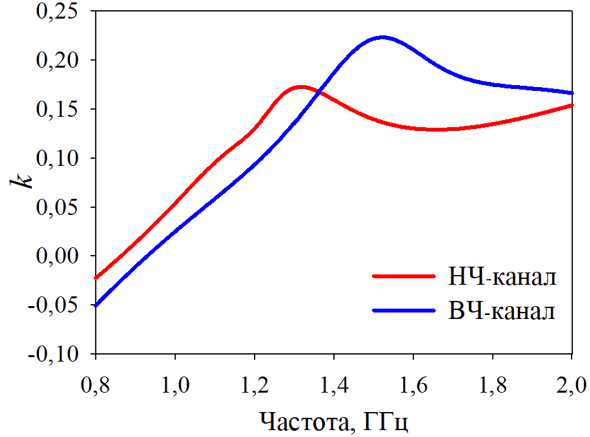
Рис. 5. Частотные зависимости коэффициентов связи для низкочастотного (красная линия) и высокочастотного (синяя линия) каналов

Fig. 5. Coupling coefficient of the matching circuit and input resonators of the low-frequency channel (red curve) and the high-frequency channel (blue) vs frequency

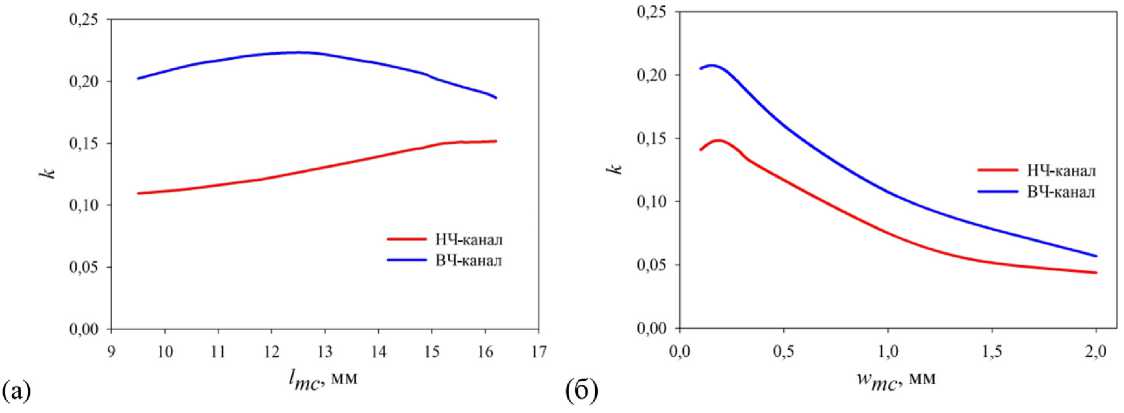
Рис. 6. Зависимости коэффициента связи от длины lmc (a) и ширины wmc (б) согласующего проводника

Fig. 6. Coupling coefficient k (a) vs length of the matching circuit lmc ; and (б) vs width of the matching circuit wmc

На рис. 7 изображены зависимости коэффициента связи согласующей цепи с входными резонаторами каналов от длины области перекрытия l_ov между проводником СЦ и входным резонатором канала. Видно, что коэффициент связи для НЧ-канала растет при увеличении l ov . Между тем в ВЧ-канале максимум k наблюдается при l_ov = 10 мм. Таким образом, подбирая величины перекрытия для каждого из каналов по отдельности, можно обеспечить необходимую величину связи. Это исследование показывает, что можно подстроить коэффициенты связи соответствующим смещением фильтров каналов диплексера вдоль проводника СЦ.

Заключение

В ходе работы была создана компьютерная программа на основе одномерных моделей субструктур каналов диплексера, с помощью которой рассчитаны частотно-зависимые ко-

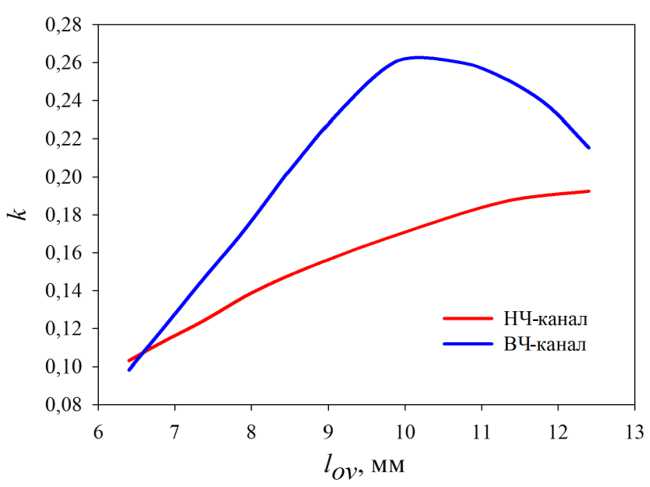
Рис. 7. Зависимости коэффициента связи от длины области перекрытия l ov согласующего проводника и входного резонатора канала

Fig. 7. Coupling coefficient k vs overlap area length lov of the matching circuit and the channel input resonator эффициенты связи, отражающие характер и величину взаимодействия в паре «согласующая цепь – входной резонатор» для низкочастотного и высокочастотного каналов. Полученные зависимости частотно-зависимых коэффициентов связи показали, что величина взаимодействия между согласующей цепью и входными резонаторами каналов достаточно велика, что подтверждает перспективность подобной конфигурации СЦ. При этом изучено влияние параметров СЦ на поведение коэффициента связи для обоих каналов. Зная поведение зависимостей коэффициента связи от параметров согласующей цепи, можно осуществлять тонкую настройку величины связи с входными резонаторами каналов, что является ключевым моментом в настройке диплексера в целом. При этом было проведено исследование, какой максимальной относительной ширины полосы пропускания каналов диплексера можно достичь, используя СЦ в виде нерезонансного отрезка МПЛ. Моделирование показало, что, используя результаты настоящего исследования, можно расширить рабочие полосы каналов как минимум в полтора раза и проектировать диплексеры со сравнительно широкими (до 15...20 %) относительными полосами пропускания каналов.