Исследование свободных движений пилы

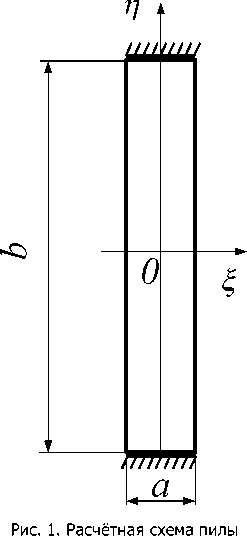
Введение. Повышенная вибрация и шумоактивность при работе пилорамы вызывает необходимость в особых условиях закрепления полотна, что позволило бы изменить амплитудно-частотные характеристики пилы с целью отстройки собственных частот от частот возбуждений, определяемых рабочим процессом. С этой целью проведём исследование собственных движений пилы при следующих условиях.

Результаты исследований. Считаем, что две боковые стороны пластины упруго защемлены, а две другие свободны, уравнение колебаний запишем в виде:

( d ⁴ w d ⁴ w

D ■      + 2

(d n⁴      d n² d ^²

d ⁴ W ) d ² W , d ² W -/ .X

+ —z- - N —_: ¹ P ■ h-- = f F (n, t ), d E⁴ J      ⁿ d n²             s t ^{2      (}', )

,                                                           n E ■ h ³

— цилиндрическая жёсткость

где h — толщина пластины; p — плотность стали; D =—_;-----

12 ( 1 -v ² )

пластины; N _n — сила предварительного натяжения пилы [1].

Продольные силы предварительного натяжения изменяют частоты её собственных колебаний. Кроме того особенности граничных условий определяются также наличием «упругого за- щемления».

Граничные условия:

w = 0

d ² W   d ² W      d w

---T- + V --- T- = C-- d n²      d ^²        d n

n = ± b

d ² W    d ² W  _

—_r + v —_r = 0 22

d ³ w        x d ³ w       , a

—5- + 2 - V)----т при E = ± —.

d ^^{3 (}     ) d E d n²             2

Таблица 1

Характеристики пилы как объекта исследования

Параметры рамной пилы	Характеристики
B — ширина пилы	160÷180
h — толщина пилы	1.6; 1.8; 2.0; 2.2; 2.5
L — длина пилы	1100; 125; 1600; 1750; 1950
D — цилиндрическая жёсткость	75÷275
σ — напряжение в серединной плоскости пилы	80÷120 МПа
N η — сила натяжения пилы	20.5÷450 кН

Эти данные будут использованы при формулировании необходимых допущений.

В первом приближении, с учётом того, что соотношение ширины и длины пластины примерно ¹ ₁₀ , воспользуемся соотношением изменённой вследствие натяжения собственной частоты, приведённым для балки:

N

^Q k = “ k Л ¹ +    ,

Nkr где шk — собственная частота для пластины при N = 0 ; N — усилие предварительного натяже- ния; Nkr — критическая сжимающая сила для балки, соответствующая продольному изгибу в плоскости колебания Nkr

π² EJ L ²

Для указанных граничных условий можно принять решение уравнения в виде (2):

w (5,n, t) = С0 cos k5 ■ cos k2n ■ exp (jtot) = Am (5, n) • exp (jtot), где j — мнимая единица; k1, k2 — волновые числа.

Вблизи границ 5 = ± a

решение представляется в виде (3):

w (5,n, t) = cos k2n ■ [Со ■ cos ki5 + f (5)] ■ exp (jtot), где f (5) — функция, позволяющая выполнить условия закрепле-

ния.

Вблизи границ n = ± Ь решение представляется в виде:

w (5,n, t) = cos ki5 ■ [Со ■ cos k2n + Ф (n)] ■ exp (jtot), где ф (n) — функция, позволяющая выполнить условия закрепле ния.

Следовательно, общее выражение Am ( 5,n ) имеет вид:

Am ( 5, n ) = С _о cos k ₁5 ■ cos k ₂n + f ( 5 ) ■ cos k ₂n + Ф ( n ) ■ cos k ₁5 .                   (5)

В средней части пластины f ( 5 ) и ф ( n ) пренебрежимо малы, поэтому выражение Am ( 5, n ) = С _о cos k ₁5 ■ cos k ₂n должно удовлетворять уравнению:

V ² V ² Am ( 5,n ) - a⁴ Am ( 5,n ) = 0,                               (6)

где V ² — оператор Лапласа; a⁴ = P h .

Подставляя выражение Am ( 5,n ) в уравнение (1) получим:

k 1 cos k ₁5 ■ С _о cos k ₂n + 2 С ₀ ( - k ² cos k ₁5 ) ■ ( - k ₂² cos k ₂n ) + k ₂⁴ cos k ₂n ■ С ₀ cos k ₁5 -

- a⁴ cos k ₁5 ■ cos k ₂n ■ С _о = 0

4      22    4    4                  2     2    2

k 1 i 2 k 1 k 2 i k 2 a — о , i ^о ес । ь a — k 1 1 k 2 .

Вблизи границ 5 = ± a

несущественно влияние функции ф ( n ) , поэтому уравнение (6)

можно записать в виде:

V ² V ² [ f ( 5 ) ■ cos k ₂n ] - a⁴ ■ f ( 5 ) ■ cos k ₂n = 0 .

После дифференцирования имеем:

f d ξ⁴

cos k ₂ n + 2

f d ξ²

■ ( - k ₂² cos k ₂n ) + f ( 5 ) ■ k 2 cos k ₂n - a⁴ cos k ₂n = 0

f - ² f ■ k + f ( 5 ) ■ ( ^k2 - " 4 ) = 0. d ξ        d ξ

Корни соответствующего характеристического уравнения получаем в виде: " 2 = k 1 ² + 2 k ₂².

Выражение для функций f ( 5 ) получим в виде:

f ( 5 ) = C 1 exp I - " 1 I 5 + 2 11 — вблизи границы 5 = - a , где " 1 = | V k 1 ² + 2 k ₂ ² 1 ;

f ( 5 ) = C 1 exp ^- 0 1 ¹ a - 5 jj — вблизи границы 5 = a , где " 1 = | Jk + 2 k ₂²1.

Аналогично рассуждая, можно определить функцию ф ( п ) .

Вблизи границ п = ± Ь несущественно влияние функции f ( 5 ) , поэтому уравнение (9)

можно записать в виде:

v ² V ² [ ф ( п ) ■ cos k 1 5 ] - a⁴ ■ ф ( п ) ■ cos k 1 5 = 0.

После дифференцирования имеем:

d ф(п) cos k5 + 2 d ф (п) ■ (-k2 cos k5) + ф (п) ■ k4 cos k 5 - "4 cos k 5 = 0 4   1    2   11     111

d^ - 2 d^» ■ k + ф (п)^( k - "4 ) = 0. dη4

Корни соответствующего характеристического уравнения получаем в виде: " 2 = 2 k 1 ² + k ₂². Выражение для функций ф ( п ) получим в виде:

ф (п) = C2 exp |-"21п + Ьjj — вблизи границы п = -Ь, где "2 = |х2k12 + k221;(11)

ф ( п ) = C ₂ exp |- "₂ 1 Ь - п jj — вблизи границы п = Ь , где "₂ = |^2 k 1 ² + k ₂²1.

Рассмотрим граничные условия на концах п = ± b :

Am ( 5,п ) = 0

d2 Am (5,п) + v d2 Am (5,п) = SAm (5,п) дп2               д52      = ^     дп, где c — жёсткость упругого защемления (4); ν — коэффициент Пуассона для стали.

Учтём, что вдоль всей стороны пластины п = -Ь функция f (5) равна нулю во всех точ ках за исключением угловых точек, поэтому можно записать:

Am ( ^5, п ) = C 0^co s k 2 b + ф ( п ) ■ cos k i^5,

Am ( ⁵ ,п )| п =- ь

¹ 2

C 0 cos k 2 ^ь + C 2 ■ cos k i 5 = 0.

Для записи второго условия определим необходимые производные:

dAm P = cos k i 5

- C ₀ k ₂ sin k ₂п - "₂ C ₂ exp I - "₂

b п + —

d ² Am ( 5,п )

d η²

= cos k 1 5 ■

- C ₀ k ₂² cos ^ .п - " 2 C 2 exp I - "₂

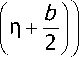
Подставляя выражения производных в уравнение (13), получим при п = - Ь

cos k15 ■ |- C ₀ k ₂² cos k ₂ Ь + a 2 C ₂ ' ■ v | C ₀ cos k ₂ Ь + C ₂ ^ ■ (-k2 cos k 1 5 ) = c ,,-("„,     , -b „ )

= d cos k 1 5 I C ₀ k ₂ sin k ₂ — - a₂ C ₂ I

Окончательно получаем систему уравнений вида:

C o cos k 2 b + C 2 = 0,

C \- k, 2 cos kb - k ²v cos kb + ck sin kb | + C | a 2 - v k ² + a, ■ c | = 0     2       2 2     1        2 2 D 2      2 2       2 2      1     2 D

.

Рассмотрим условия свободных краёв:

д ² Am ( 5,п ) _{+ V} д ² Am ( 5,п ) = 0 д ³ Am ( 5,п )

5 5 2               д п²                д 5 3

д ³ Am ( 5,п )     , а

+ (2 - V)----- Ц— при 5 = + — .

⁽      ) д 5 д п²                 2

Учтём, что вдоль всей стороны пластины 5 = - а функция Ф ( п ) равна нулю во всех точ-

ках за исключением угловых точек, поэтому можно записать:

Am ( 5, n )| = [ C 0 cos k 1 5 + f ( 5 ) ] ■ cos k 2 n = 0 ,

Am M 5=- a

C 0 cos k a + C 1

■ cos k ₂n = 0 .

Для записи второго условия определим необходимые производные:

d ² Am ( 5,n )

----"^---^L = cos ^П ■

- C ₀ k ² cos k 1 5 - a 2 C exp I - 0 1 I 5 + 0

,

d ² Am ( 5,n )

d η²

= cos k 1 5 ■

- C ₀ k ₂² cos k ₂n - o 2 C ₂ exp I - a₂

d ³ Am ( 5,n )

d ξ³

= cos k ₂n ■

Ck ³ sin k 5 - 0 3 C exp |- o, 1 5 + a 01       1      1 1           1

d³ Am ( 5,n ) d η² d ξ

- k ₂² cos k ₂n ■

- Ck sin k 5 - 0, C exp I - 0, 1 5 + a 01     1    11        1

Граничные условия на свободных сторонах, учитывая, что косинус является чётной функцией, записываем в виде:

cos k2n ■ |-C0k2 cos k1 a + a2C1 ] - vk22 cos k151C0 cos k1 a + C1 ] = 0 , cos k2n ■ \-C0k1 sin k1 -^ - a3C| + (2 - v) k22 cos k2n \-C0 sin k1 -0- + a1C11 = 0 .

Окончательно получаем систему уравнений вида:

C ₀ 1 - k cos k 1 О - v k ₂² cos k 1 0 1 + C 1 ( a 2 - v k ₂ ² ) = 0,

C 0 ■ | k 1 sin k i О + ( 2 - v ) k 2 sin k 1 0 1 + C 1 ( a 1 ( 2 - v ) k 2 - 0³ ) = 0, где 0 1 = V k i + 2 k ₂² ; a₂ = 7 2k 2 + k ₂² .

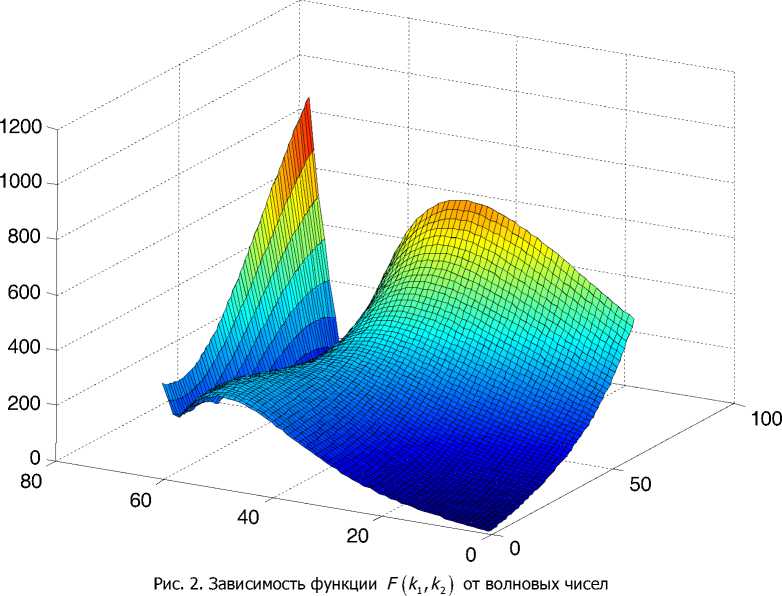
Для одновременного выполнения приведённых уравнений необходимо, чтобы определители этих уравнений равнялись нулю, то есть решения следующих уравнений:

F1 =

cos k

- k 2 cos k ₂

— - k ²v cos kb + ck sin kb 2     1        2 2 D 2     2 2

a² 2 - vk ² + a₂ ■ c

2     1     2 D

= 0,

F 2 =

- k ² cos ka - vk ² cos k a

1         1 2        2         1 2

k ³ sin k a + (2 - v) k ² sin k a

1        1 2                 2        1 2

a 2 - ^{v k} 2

^a i ( 2 ^{- v} ) ^k2 ^{- a}3

= 0 .

Для обоснования дальнейших рассуждений был использован пакет прикладных программ MatLab. В результате была построена поверхность, определяемая выражением: F(k ₁ ,k ₂ ) = abs ( F1(k 1 ,k ,) ) + abs ( F2(k 1 ,k ,)^ ) (рис. 2).

Как следует из анализа полученной поверхности, «овраг» существует. Для того чтобы уточнить начальные значения волновых чисел, строим контурный график (рис. 3). Как видно из него, значения волновых чисел лежат около значений k ₁ = 5, k ₂ = 5 (графики построены относительно индексов, значит, при расчётном шаге 0,1 индексу 50 соответствует волновое число 5).

Расчёт, проведённый в среде MatLab с использованием встроенной функции «fsolve», позволил получить следующие результаты:

k =	fval =	ex =
5.194	8.3576e-015	1
5.0265	-2.2737e-012

Заключение. Как видно из полученных результатов, значение ошибки решения задачи «fval» имеет порядок 10-12 +10-15, то есть точность вполне достаточна. Значение «ех» является положи- тельным числом, что, по условиям MatLab’а, означает успешное прохождение расчёта. Полученные результаты позволяют использовать разработанные программы для проведения математического моделирования как свободных, так и вынужденных движений пилы.

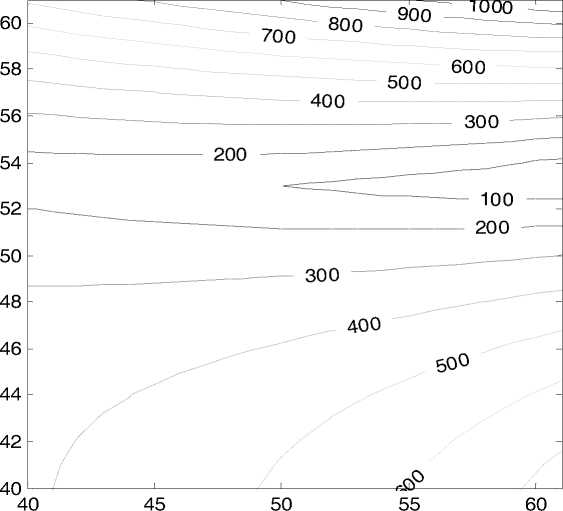
Рис. 3. Контурный график