Исследование свободных колебаний микромеханического гироскопа с учетом неортогональности осей торсионов

УДК 531.383                                              

Введение. Разработка высокоточных микромеханических инерциальных датчиков, в том числе микромеханических гироскопов (ММГ), применяемых для решения задач навигации и управления движением летательных аппаратов и мобильных роботов, является актуальной задачей приборостроения [1]. К достоинствам ММГ относятся малые масса и размеры, а также низкая стоимость по сравнению с гироскопами, основанными на других физических принципах. Однако к главным недостаткам ММГ относятся изменчивость его метрологических характеристик и низкая точность измерений параметров углового движения объекта (угловой скорости и угла поворота). Принцип функционирования вибрационных гироскопов основан на свойстве маятника Фуко сохранять плоскость малых колебаний неподвижной в инерциальном пространстве [2].

Основы теории гироскопов класса обобщенного маятника Фуко, к числу которых относятся и ММГ, изложены работах [2–5]. В них описаны различные конструктивные схемы построения ММГ, исследовано влияние инструментальных погрешностей изготовления и изменяющихся условий функционирования на динамику гироскопа. Принципиальной особенностью гироскопов класса обобщенного маятника Фуко является нелинейность, обусловленная конечными колебаниями чувствительных элементов (ЧЭ) или физической нелинейностью, связанной с особенностями системы управления колебаниями [2–6].

Исследования, посвященные динамике и конструированию ММГ, были опубликованы и в работах зарубежных авторов [6–8]. Так, например, в публикациях [6, 8] получена формула для оценки уходов гироскопа, основанная на использовании разработанной математической модели движения, которая описывает медленное изменение тороидальных координат колебаний ЧЭ. В работах [0, 7] обсуждаются вопросы изготовления ММГ и анализируются уравнения его малых колебаний. В статье [0] составляются уравнения движения ММГ с угловым (R-R-типа) и линейным (L-L-типа) осцилляторными видами движения ЧЭ. В указанной статье проводится сравнительный анализ динамики таких приборов в рамках линейных моделей и даны рекомендации по выбору параметров ММГ, исходя из условий повышения чувствительности и обеспечения требуемой полосы пропускания, а также требований к линейности масштабного коэффициента.

При проектировании ММГ разработчики стремятся использовать явление внутреннего резонанса в системе, обусловленное совмещением собственных частот колебаний ЧЭ [3, 4]. Однако в работах [0, 7] отмечается, что погрешности технологии изготовления, неизвестные и непредсказуемые отклонения элементов конструкции от проектных положений приводят к дополнительным погрешностям в измерениях прибора.

Для повышения точности измерения угловой скорости ММГ поставлена цель: исследовать свободные колебания (при отсутствии управления) ЧЭ ММГ R-R-типа с учетом эффектов, возникающих из-за неортогональности осей торсионов. Этот дефект появляется в виду несовершенства технологии изготовления прибора. Ставятся задачи разработки новой математической модели динамики ММГ с учетом неортогональности осей торсионов, оценки ухода прибора и описания влияния неортогональности осей торсионов на динамику ЧЭ ММГ.

Материалы и методы. Рассматривается модельная конструкция вибрационного ММГ R-R-типа — конструкция с промежуточной рамкой в соответствии с классификацией из источника [3]. Кинематическая схема гироскопа (рис. 1) реализована в виде двухстепенного карданного подвеса ЧЭ.

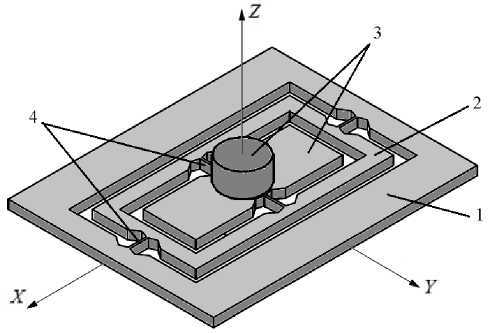
Рис. 1. Конструктивная схема прибора: 1 — основание (корпус); 2 — промежуточная (внешняя) рамка; 3 — чувствительный элемент, состоящий из сбалансированной пластины и инерционной массы; 4 — торсионы

Для описания положения ЧЭ введем системы координат (рис. 2), связанных: с корпусом прибора — OXYZ ; с внешней рамкой упругого подвеса — Ox ₁ y ₁ z ₁; с сбалансированной пластиной — Oxyz . Причем OZ является осью чувствительности гироскопа, а система координат Ox 2 y 2 z 2 отличается от системы Ox 1 y 1 z 1 поворотом на постоянный угол неортогональности всех торсионов. В представленных системах начало координат соответствует точке O и находится в геометрическом центре сбалансированной пластины.

J 1 x ,

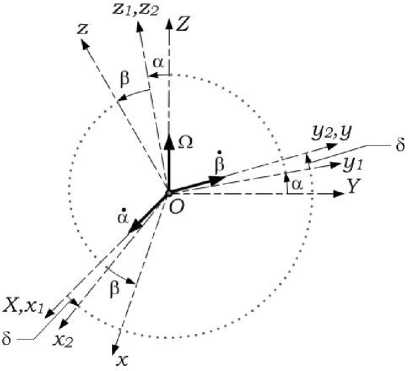
Рис. 2. Системы координат

Механика

В системе Ox ₁ y ₁ z ₁ зададим осевые моменты инерции промежуточной рамки J 1 x , J 1 y , J 1 z , а в системе Oxyz — осевые моменты инерции ЧЭ J 2 x , J 2 y , J 2 z . Отметим, что в данной работе оси систем координат Ox ₁ y ₁ z ₁ и Oxyz считаются главными центральными осями инерции промежуточной рамки и ЧЭ соответственно.

При моделировании движения ЧЭ принимается допущение, что конструкция торсионов обеспечивает бесконечную жесткость на изгиб. Положение ЧЭ относительно основания ММГ опишем двумя обобщенными координатами — углами а ир , а также малым постоянным углом 5 , характеризующим неортогональность осей торсионов (рис. 2). Взаимное расположение систем координат определяется последовательностью элементарных поворотов:

OXYZ ——> Ox1 y1 zx ——► Ox2 y 2 z2 ——> Oxyz, xz1y2

где под каждой стрелкой указывается ось, вокруг которой происходит поворот против хода часовой стрелки на угол, указанный над соответствующей стрелкой.

Составим уравнения динамики ЧЭ ММГ в форме уравнений Лагранжа 2-го рода [9, 10]:

d । d L dt (д а

д L    дФ d ( д L

д l   дФ

да    да    dt (д р J д р     д в ,

где L = T - П — функция Лагранжа; Т и П — кинетическая и потенциальная энергии системы соответственно; Ф — диссипативная функция, характеризующая потери на внутреннее трение. Выражения для этих величин имеют вид:

^r1 y sin² а + J 1 _z cos² a ) Q ² ) ,

Ф

где d_a , dp — коэффициенты трения; е_а , е _р — коэффициенты жесткости торсионов.

Выражения для проекций ω x , ω y , ω z угловой скорости ЧЭ на подвижные оси x , y , z имеют вид: to x = а cos в cos 5 - Q cos а sinв + Q sin а cos в sin 5,

toy = в + Q sin а cos 5 - а sin 5, toz = а sin в cos 5 + Q cos а cos в + Q sin а sin в sin 5.

Учитывая малость углов а , в и 5 , тригонометрические функции в выражениях (2) и (3) от указанных углов можно заменить их разложениями в ряд Тейлора, ограничившись слагаемыми до первого порядка малости. Тогда получим уравнения малых колебаний из уравнений движения (1), записанных с учетом выражений (2) и (3).

Используя формализм Лагранжа [9] в случае постоянной угловой скорости основания, получаем уравнения малых колебаний ЧЭ, записанные с точностью до слагаемых первого порядка малости в виде:

ωj                       ω а + m2 а = j1Qв - аа + 15 5в,    в + m2 в = -j2 Qa---в + 5а,

а          Qa    j2            в            Qe где введены следующие обозначения (аналогично тому, как это выполнено в статье [11]):

2 x

d _β

ω_β J _{2 y}

Здесь j 1 , j ₂ — безразмерные моменты инерции упругого подвеса; to , to и Qa , Qp — собственные частоты колебаний и добротности по углам а , в соответственно.

При выводе уравнений колебаний (4) угловая скорость корпуса гироскопа Q считалась малой относительно собственной частоты ^ , т.е. |Q| <<  m_a , а также угол 5 полагался малой величиной, т. е. 5 <<  1. Отметим, что в уравнениях (4) отброшены слагаемые, обусловленные наличием геометрической нелинейности ММГ. Влияние нелинейности геометрии движения ЧЭ на динамику ММГ R-R-типа описано в монографии [5].

Принимая во внимание, что правые части уравнений (4) являются малыми возмущениями, т. е. а + m 2 а = O ( s ) , то с точностью до слагаемых первого порядка малости можно записать: а = - ю 2 а + O ( ^ ) . Таким образом, из правой части уравнений (4) исключаются вторые производные углов а и в .

Рассмотрим случай изотропного упругого подвеса, т. е. равенства собственных частот колебаний и равных добротностей:

«а = «в = «0,    Qa = Qp = Q , где «0 — характерное значение собственной частоты колебаний; Q — характерное значение добротности.

Отметим, что случай наличия разнодобротнсти (Qa Ф Qp ) и малой разночастотности (« Ф «р ) при исследовании свободных колебаний ЧЭ ММГ рассмотрен в статье [11]. При введенных обозначениях и принятых допущениях запишем уравнения движения ЧЭ с точностью до слагаемых первого порядка малости в безразмерном виде:

а + о ’ а = j_x И в - Q 'о_о а - -j ¹- S ш 2 в, ^{01 0} j 2 ⁰ (5)

Р + ^ 0 в = — j 2 И а — Q ^р — дю 0 а .

Отметим, что система уравнений (5) приводится к стандартной форме записи регулярно возмущенной системы дифференциальных уравнений с одной быстрой угловой переменной [12, 14]. Одним из распространенных способов нахождения решения регулярно возмущенных систем является использование асимптотических методов разделения движений [12–15].

Решение нелинейных уравнений (5) получим с помощью методики осреднения Крылова — Боголюбова [13], а в качестве медленно меняющихся переменных будем использовать переменные Ван-дер-Поля [12] p 1 , q 1 , p 2 , q 2 :

а = р1 sin (®01) + q1 cos (®01), а = ®0 р1 cos (ю01) — w0 q1 sin (w01), в = р2 sin ( w01) + q2 cos ( ю01), в = ю0P2 cos (ю01)- ю0q2 sin ( ю01).

С помощью процедуры осреднения [14, 15] по явно входящему времени, получаем осредненную систему дифференциальных уравнений, разрешенную относительно производных медленных переменных Вандер-Поля:

р ‘ =	1 ^—1      j1 и — -Q р 1 +--- p 2 2       2 « 0	- Sq 2 j 2 q 2 ,	q ‘ = -	1    — i      j1 И       j 1 S --Q q 1 + Z-- q 2 +T- р 2 , 2        2 « 0      2 j 2	(6)
р 2 =	1 ^1     j 2 И — -Q р 2 —-- р 1 2       2 « 0	s - 2 q 1,	q 2 =	1   — 1     j 2 И      s — -Q q 2 — —q 1 +- р 1 - 2       2 « 0    2

Штрихом в уравнениях (6) обозначено дифференцирование по безразмерному времени т = « ₀ 1 .

Полученная модель в виде линейных дифференциальных уравнений описывает свободные колебания

ЧЭ гироскопа на подвижном основании. Решение системы уравнений (6) можно записать в виде:

' ^р 20 - ’О ) Sin( Т , 22

р ( ^т ) = exp

q 1 ( т ) = exp ^	— 2 Q ].	q ,0 cos(V v ‘ + YT h jjLVl-^^^, j 2     V V 2 + Y 1	$ in ( 4V 2 + Y 2т ) ,
р 2 ( т ) = exP |	Т 1 .— 2 Q )	р 20 cos ( 4777 т ) — в: .y^si L      v        7 V1    7v + y	sin ( 4v 2 + Y 2т )
f q 2 ( т ) = exp 1	— т 1 2 Q J	q „cos ( V2 ■ + ? 2 r )   j .( ^q^, L      V          j 4h   ^v 2 + Y2	5 in ( 4V 2 + Y2т )

где р ₁₀ = p 1 ( 0 ) , р ₂₀ = р ₂ ( 0 ) , q ₁₀ = q 1 ( 0 ) , q ₂₀ = q ₂ ( 0) — начальные условия; безразмерная угловая скорость основания прибора v = ^ j 1 j ₂ q/ ( 2ю₀ ) ; параметр, характеризующий неортогональность осей торсионов у = ^{j ( 2} V j T) .

Вторые слагаемые в формулах (7) характеризуют перекрестное влияние первичных колебаний на вторичные колебания и наоборот. Отметим, что в случае ортогональных осей торсионов, когда у = 0, решение (7) совпадает с результатами работы [5].

Полученные аналитические решения (7) уравнений колебаний представляют интерес для разработки методик идентификации параметров, а также прогнозирования ухода гироскопа и его учета при использовании методики алгоритмической компенсации погрешностей.

Механика

Результаты исследования. Для валидации разработанной модели сравним результаты моделирования, вычисленные по формулам (7), с экспериментальными данными. Измерительная информация получена с помощью системы наблюдения. В качестве измерительной информации электростатических датчиков имеем переменные Ван-дер-Поля p 1 , q 1 , p 2 , q 2 .

В эксперименте использован образец прибора со следующими параметрами математической модели при неподвижном основании ( v = 0): Q = 3856, j₁ = j 2 = 1, у = 0,2 - 10 ^{- 5}, в качестве начальных условий для переменных Ван-дер-Поля выбраны значения равные измерениям в начальный момент времени:

р ₁₀ = 13,467 - 10 ^{- 3}, q ₁₀ = 20,429 - 10 ^{- 3}, р ₂₀ = 0,787 - 10 3 , q ₂₀ = 1,172 - 10 ^{- 3}.

Значение параметра у соответствует углу неортогональности осей торсионов 5 равного одной угловой секунде. Графическое представление зависимостей переменных Ван-дер-Поля р 1 ( г ) , q₁ ( г ) , р ₂ ( г ) , q ₂ ( г ) медленно меняющихся с течением безразмерного времени, приведено на рисунке 3.

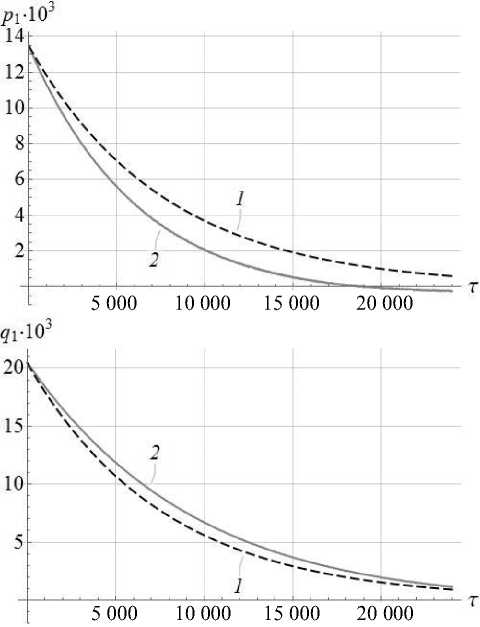
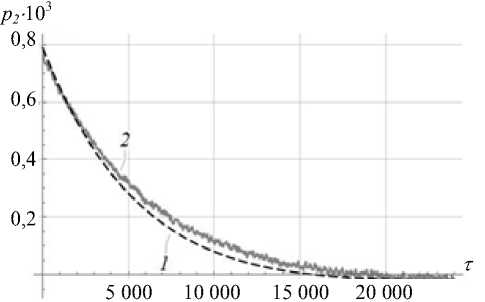
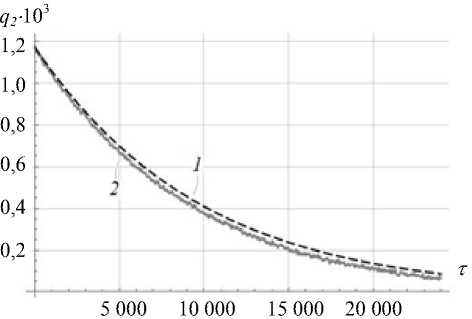
Рис. 3. Зависимости переменных Ван-дер-Поля: 1 — результаты моделирования; 2 — экспериментальные данные

Графики (рис. 3) демонстрируют значительное совпадение зависимостей для переменных p2,  q2 , полученных по результатам моделирования, с экспериментальными данными. Зависимости для переменных p1 ,  q1 , полученные по результатам моделирования, качественно согласуются с данными эксперимента, а

наблюдаемые небольшие количественные отклонения могут быть обусловлены нелинейными эффектами, такими как нелинейность геометрии движения ЧЭ [5], или явлениями разнодобротности, разночастотности и погрешностью смещения инерционной массы [11]. Рассмотрение нелинейных эффектов, влияющих на динамику ММГ, при построении математических моделей колебаний ЧЭ увеличивает точность микромеханических датчиков в составе инерциальных навигационных систем [2].

Уход гироскопа из-за нелинейных эффектов и других инструментальных погрешностей будем оценивать с помощью вспомогательного функционала I [5, 6, 8]:

• ² j T ( q 1 q 2 + Р 1 р 2 ) j 2 ( q 2 + Р 1 ² ) ^{- j} 1 ( q 2 + р 2 ² ) ,

  
  

который связан с углом 6 через соотношение:

9 = ¹ arctan

(I).

Причем этот параметр пропорционален интегралу от угловой скорости:

е = - j j ^ C r , ) d T _x .

С помощью формулы (8), учитывая решение (7), можно оценивать уход гироскопа, связанный с неортогональностью осей торсионов, возникшей из-за несовершенства технологии изготовления. На рис. 4. представлены зависимости функционала I от безразмерного времени по результатам эксперимента и расчета по формуле (8).

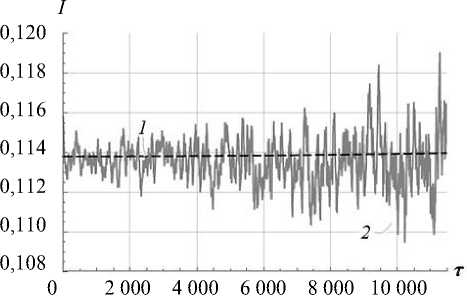
Рис. 4. Зависимость функционала I ( т ) : 1 — результаты моделирования; 2 — экспериментальные данные

Близость оценки ухода (рис. 4) и переменных Ван-дер-Поля (рис. 3), полученных аналитически, с экспериментальными данными характеризуют хорошую точность построенной модели, особенно если учесть тот факт, что в ней пренебрегались нелинейные эффекты, а также явления разночастотности и разнодобротности. Несмотря на указанные пренебрежения, модель позволяет построить методики идентификации параметров, с помощью которых можно уточнить зависимости, полученные при моделировании. Применение методик идентификации параметров математической модели приведет к повышению точности ММГ в режиме вынужденных колебаний, который является рабочим режимом гироскопов.

Обсуждение и заключения. Построена новая математическая модель ММГ R-R-типа для режима свободных колебаний ЧЭ. В модели учитывается неортогональность осей торсионов, возникающая в следствие технологической невозможности обеспечить высокую точность изготовления прибора. Получена формула оценки угла прецессии при подвижном основании прибора. Посредством сравнения результатов моделирования с данными эксперимента проведена валидация математической модели ММГ. Показано, что неортогональность осей торсионов приводит к перекрестному влиянию первичных колебаний на величину вторичных колебаний и наоборот. Результаты работы могут быть использованы в алгоритме аналитической компенсации погрешности гироскопа с целью повышения точности ММГ.