Исследование свойств композитного материала на основе эпоксидной смолы и полидисперсной смеси кварцевого песка

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

Эпоксидные полимеры по целому ряду свойств выделяются среди прочих полимерных материалов, играя важную роль в аэрокосмической, автомобильной, судостроительной и других отраслях промышленности. Широкое их применение в технике связано, во-первых, с высокой технологичностью эпоксидных смол, во-вторых, с уникальным сочетанием эксплуатационных характеристик продуктов их отверждения [1].

Особое место занимают композиционные материалы, созданные на их основе, которые состоят из двух или более компонентов с границей раздела между ними. Каждый из компонентов вносит вклад в структуру и свойства композиционного материала. В связи с этим такие материалы становятся все более и более востребованными в современной промышленности, поскольку им можно придавать новые или улучшенные свойства.

В литературе достаточно широко представлены исследования физико-химических, теплофизических и электрических характеристик ряда полимерных материалов, допированных различными наномодификаторами: углеродными нанотрубками, нановолокнами, фуллеренами и графенами (см., например, [2-4]). Влияние нанодобавок на механические свойства композита обычно невелико (не более 30 %) [5].

Вместе с тем находят широкое применение и композиционные материалы с макроскопическими наполнителями, такими, например, как кварцевый песок, луз- га, опилки, полимерные порошки, шламы, стружки -прикладное, но крайне востребованное направление материаловедения [6-9]. Это объясняется доступностью данных добавок (карьеры, отходы производства и др.). Такие композиты используются при разработке новых составов асфальтобетонов, способных выдерживать возрастающие нагрузки [10; 11], для изделий строительного и декоративного назначения [12], для восстановления деталей отвалов [13], для устранения дефектов в виде износов и сквозных протираний поверхности деталей со сложнопрофильной поверхностью [14].

Влияние наполнителя на механические характеристики эпоксидополимерных композиционных материалов рассмотрены в работах [15-19]. Показано, что наполнители играют большую роль при формировании структуры и свойств полимерных композиций. Числовые результаты исследований значительно различаются, но общая тенденция одинакова: при незначительном снижении прочности при сжатии и растяжении они обладают высокими показателями демпфирующих характеристик, способствуют росту стойкости к истиранию и к набуханию в агрессивных средах.

В приведенных выше исследованиях, как правило, не характеризуется структура песчаной смеси, за исключением среднего размера частиц, в то время как свойства полимерных композиционных материалов определяются структурой матрицы, типом, свойствами и характером распределения частиц по объёму и, наконец, величиной и природой межфазного слоя. Перво- очередной задачей является оптимизация структуры и свойств композиционных материалов, достижение которой позволяет одновременно повысить их экономичность, надежность и долговечность.

Песок различной дисперсности и чистоты можно считать основным наполнителем макроскопических композитов, особенно если учесть его объёмы потребления в строительстве. Фактически песок, представляющий собой кварцевые искажённые микро- и мезосферы, является типичной пористой средой различной дисперсности и чистоты. Важнейшими характеристиками структуры пористых и дисперсных веществ и материалов являются: полидисперсность, удельная поверхность, размер пор, открытая пористость и коэффициент проницаемости. Каждая из этих взаимосвязанных характеристик может быть предварительно измерена или рассчитана для конкретной дисперсной среды, используемой при производстве композита и служить критерием эффективности и пригодности данного материала как к заданным условиям эксплуатации, так и параметров технологического процесса его получения.

Оценка влияния содержания кварцевого песка на прочность мелкозернистых композиционных материалов рассмотрено в работе [20]. В статье представлена сравнительная оценка кинетики набора прочности при изгибе и сжатии мелкозернистых бетонов при различном содержании песчаного заполнителя. Установлено, что для получения мелкозернистых композитов оптимальной прочности необходимо равное соотношение таких компонентов смеси, как вяжущее вещество и кварцевый песок.

Влияние дисперсности песка на абразивную износостойкость композита с эпоксидной основой рассмотрено в работе [21]. Показано, что увеличение эффективного диаметра частиц песка в композите на основе эпоксидной смолы способствует росту износостойкости независимо от соотношения компонентов. Наибольшую стойкость к абразивному изнашиванию имеет состав при содержании 60 мас. ч. песка с дисперсностью 1 мм.

Исследование влияния размеров частиц дисперсного наполнителя на пористость эпоксидного композита выполнено в работе [22]. Установлено, что применение в качестве наполнителя кварцевого песка с размером частиц 0,063 мм позволяет методом смешения получить материалы, экспериментальное значение пористости которых не превышает расчетное значение.

В приведенных выше исследованиях, как правило, не проводится сопоставление механических свойств тех или иных композитных материалов с характеристиками песчаной смеси, таких как полидисперсность, открытая пористость, проницаемость.

С точки зрения промышленного производства, когда используется наполнитель с одного карьера, это оказывается оправданным, так как эмпирическим путем можно подобрать необходимое соотношение компонентов, обеспечивающее нужные механические свойства композита. Эту задачу можно минимизировать, если исследовать зависимость механических свойств композитных материалов от числовых характеристик наполнителя.

В настоящей работе сделана попытка анализа влияния таких характеристик, как полидисперсность, открытая пористость, проницаемость песчаной смеси, на прочность на растяжение и сжатия получаемых композиционных материалов. В рамках работы проведено исследование распределения частиц по размеру кварцевого песка и его влияние на пористость и проницаемость полидисперсной смеси, а также выполнены измерения механических свойств композита в зависимости от дисперсного состава наполнителя.

Структура полидисперсной смеси

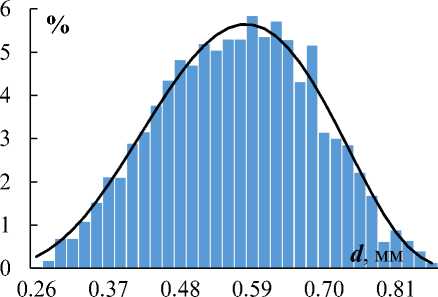
В качестве дисперсного материала использовались два сорта кварцевого песка с двумя характерными размерами частиц, условно названные «мелкими» и «крупными». Для исследования статистических характеристик порошков применялся поляризационный микроскоп Olympus BX51-P. На дно чашки Петри помещались исследуемые образцы, образующие тонкий слой. В ходе экспериментов на камеру записывались серии изображений, полученных при просвечивании рабочего слоя рассеянным светом. Серии изображений обрабатывались на компьютере при помощи программы ImageJ. В целом частицы имели неправильную геометрическую форму. При обработке изображений форма частиц аппроксимировалась окружностью с эквивалентной частице площадью сечения. На основе обработки серий изображений построены гистограммы распределения по диаметру частиц, на основании которых были определены их статистические свойства. Примеры микрофотографий частиц и соответствующие им гистограммы распределения частиц по размерам показаны на рис. 1, а , b , рис. 2, а , b .

Анализ показывает, что исследуемые образцы имеют следующие характеристики: «мелкие» – средний диаметр 0,15 мм, медиана – 0,146, мода – 0,124 (выборка из 1150 частиц); «крупные» – средний диаметр 0,53 мм, медиана – 0,526, мода – 0,568 (выборка из 1200 частиц).

Для определения наличия разницы между средними значениями двух независимых выборок был рассчитан t -критерий Стьюдента, значение которого составило 102, что значительно превышает критическое табличное значение 3,473 и свидетельствует о статистической различимости этих двух выборок.

а

%

d , мм

.07 0.11 0.16 0.20 0.25 0.29

Эксперимент ^^^^^» Аппроксимация

b

a

Рис. 2. Фотография «крупных» частиц ( a ) и распределение «крупных» частиц по диаметру ( b )

Fig. 2. The coarse particles ( a ), the distribution of diameters of coarse particles ( b )

Рис. 1. Фотография «мелких» частиц ( а ) и распределение «мелких» частиц по диаметру ( b )

Fig. 1. The fine particles ( а ), the distribution diameters of the fine particle ( b )

■ Эксперимент ^^^^^^м Аппроксимация

b

2.    Характеристики полидисперсной смеси в приближении модели пористой среды

Будем рассматривать полидисперсную смесь, в которой варьируется массовая доля «мелкой» фракции от 0 до 1 с шагом 0,1. Для анализа свойств получаемой смеси воспользуемся такими количественными характеристиками модели пористой среды, как пористость и проницаемость. Под «пористостью» будем понимать отношение свободного пространства не занятого частицами песка к общему объему, занятому песчаной смесью.

Для расчета параметров пористости материалов применяют различные модели фильтрации в пористой среде [23]. Наиболее простым является метод заполнения пор жидкостью [24], который позволяет рассчитать открытую пористость материалов, исходя из объёма тела и жидкости, заполнившей до насыщения поры образца. Объём жидкости определяется по изменению веса сухого образца после насыщения его жидкостью известной плотности.

Определение пористости производилось по следующей схеме. Исходные образцы и их смеси помещались в квадратный контейнер объемом V 0 = 4,2 см³ с отверстием в нижней его части. Снизу и сверху навески ограничивались мелкой металлической сеткой для предотвращения изменения объема образца при заполнении его жидкостью. Далее контейнер заполнялся дистиллированной водой, часть которой стекала из нижнего отверстия, до полного пропитывания материала. Массы пустого контейнера, контейнера с сухим веществом и пропитанным жидкостью, необходимые для расчета объема воды, измерялись с помощью аналитических весов ЛВ-210А 2-го класса точности. Открытая пористость m определялась как отношение объема воды в порах V к объему контейнера V 0 . Для каждой концентрации проводилась серия измерений, результаты которых усреднялись. В результате была построена зависимость пористости m от доли «мелких» частиц φ, показанная на рис. 3.

о m, %

% , "мелких" частиц

Рис. 3. Значения пористости материала в зависимости от доли «мелких» частиц

Fig. 3. The material porosity values depending on the fine particle proportion

Откуда видно, что в однородной смеси, состоящей только из «мелкой» или только из «крупной» фракции пористость практически одинакова (отличаются в пределах погрешности измерения на 1 %). Пористость – безразмерная величина со значениями в интервале 0 <  m < 1, характеризующая форму и взаимное расположение зёрен (пор) и потому одинаковая для геометрически подобных сред. Это подтверждается элементарным расчетом для случая частиц в виде шаров одинаковых радиусов. С другой стороны, в этой зависимости имеется четко выраженный локальный минимум при значении доли «мелких» частиц около 40 %, составляющий более 15 % от максимального значения.

Коэффициент проницаемости является одним из основных структурно-зависимых показателей пористых проницаемых материалов, определяющим эффективность и пригодность данного материала к заданным условиям эксплуатации и представляющим зачастую функцию оптимизации как структуры порового пространства материала, так и параметров технологического процесса его получения.

Проницаемость будем оценивать в контексте модели Дарси [25]. Закон Дарси предполагает линейную связь между градиентом давления и скоростью фильтрации флюида. С точки зрения экспериментальной проверки его можно выразить следующей формулой k S Дp ηL

где Q – объемный расход жидкости, k – коэффициент проницаемости пористой среды, S – площадь поперечного сечения образца, A p - перепад давления, п — динамическая вязкость жидкости, L – длина образца пористой среды.

Принцип расчета проницаемости пористой среды в лабораторных условиях состоит в непосредственном измерении расхода жидкости определенной вязкости через единицу площади образца среды и градиента дав- ления, вызывающего это течение, а также в расчете коэффициента проницаемости по уравнению (1).

Экспериментальная установка в целом идентична классическим вертикальным установкам [24; 25]. Образец (фрагмент материала) заполняется в цилиндрическую испытательную ячейку, размеры и конструкция которой может изменяться. Ячейка выполнена из прозрачного материала, позволяющего визуально контролировать процесс течения рабочей жидкости через испытуемый материал. Снизу и сверху навески ограничивались мелкой металлической сеткой для предотвращения изменения объема образца при протекании жидкости. Испытательная ячейка соединяется фланцем с широким резервуаром для напорной жидкости. Работа установки заключается в заполнении ее рабочей жидкостью (дистиллированная вода) и пропускании указанной жидкости в стационарном режиме сквозь поровое пространство испытуемого материала с одновременным замером потерь давления и массы протекающей жидкости. Масса протекающей жидкости измерялась при помощи микровесов. Через равные промежутки времени показания микровесов фиксировались на видеокамеру, затем оцифровывались и анализировались. Масса протекания через каждый образец измерялось не менее 6 раз: по 3 раза для разной высоты напорной жидкости, которые затем усреднялись.

Типичные результаты зависимости массы (объёма) протекающей через образец жидкости от времени протекания показан на рис. 4.

Угловой коэффициент таких кривых соответствует искомому объемному расходу жидкости Q . Подставляя объемный расход жидкости и параметры установки в формулу (1) вычислим коэффициент проницаемости k . Результаты вычислений в зависимости от процентного содержания «мелкой» фракции показаны на рис. 5, а .

Из рис. 5, а , видно, что наблюдается практически линейная связь эффективной вязкости от значения доли «мелких» частиц. Этот факт легко интерпретировать, используя понятие вязкого трения в приближении Стокса.

q, см3

t , с

0            40           80           120          160

Рис.  4. Зависимости объема протекающей жидкости от времени протекания для разных соотношений фракций «мелкого» песка: сверху вниз 0, 20, 30, 60, 100 %

Fig. 4. The flowing liquid volume dependences on the flowing time for fine sand fractions different ratios: top-down 0, 20, 30, 60, 100 %

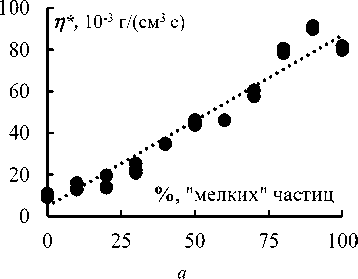
Рис. 5. Изменение эффективной вязкости от процентного содержания «мелкой» фракции ( a ); изменение коэффициента проницаемости от процентного содержания «мелкой» фракции ( b )

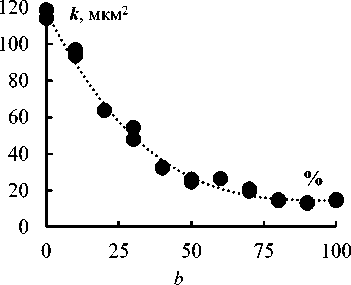
Fig 5. The effective viscosity changing from the fine fraction percentage ( a ); the permeability coefficient changing from the fine fraction percentage ( b )

Модель Стокса для определения силы вязкого трения действующей на сферу небольшого радиуса, обтекаемого жидкость с небольшой скоростью (число Рейнольдса Re→0) имеет вид: F = 6πη rV , где η – динамическая вязкость жидкости, r – радиус сферы, V – характерная скорость жидкости. Можно предположить, что для ансамбля частиц (смеси) сферической формы с характерными радиусами r 1 и r 2 сила вязкого трения пропорциональна φ С 1 r 1 + (1 – φ) C 2 r 2 , где φ – доля частиц радиуса r 1 . В этом случае эффективная вязкость пористой среды η* = η/ k ведет себя подобным образом, то есть линейно зависит от доли «мелких» частиц, что и подтверждается результатами эксперимента (см. рис. 5, а ). Тогда экспериментальная от φ зависимость самой проницаемости хорошо описывается гиперболой (см. рис. 5, b ).

Полученные характеристики пористой среды с помощью уравнений Дарси и Пуазейля могут быть объединены в одну величину, называемую характерный радиус пор r . Для идеальной пористой среды это позволяет получить взаимосвязь проницаемости и пористости [26]

r = Д • m

Это уравнение, характеризующее взаимосвязь между пористостью, проницаемостью и радиусом порового канала и справедливо только для идеальной пористой среды, например, кварцевый мономиктовый песок, представленный на 90 % одним минералом.

В большинстве случаев пористые среды обладают нерегулярной внутренней структурой. Данное обстоятельство затрудняет подробное описание фильтрационных течений прямыми методами гидродинамики. В работе [29] для оценки эффективного радиуса реальных пород предложено учитывать структурный коэффициент f , описывающий извилистость порового пространства, который можно оценить, используя данные измерений электрического сопротивления горных пород:

где f =

0 . 5035

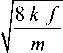
Изменение эффективного радиуса пор в зависимости от доли «мелких» частиц, вычисленное по формуле (2), показано на рис. 6.

r , мкм

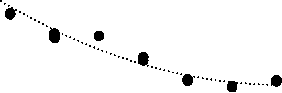
% , "мелких" частиц

Рис. 6. Изменение эффективного радиуса пор в зависимости от доли «мелких» частиц

Fig. 6. The effective pore radius changing depending on the fine particle proportion

Механические свойства композита

Для измерения механической прочности на растяжение были изготовлены стандартные лопатки по ГОСТ ISO 37 (тип.2) [28].

При изготовлении образцов твердая фракция с нужной концентрацией «мелких» частиц засыпалась в специальную форму и пропитывалась клеевым составом (не перемешивалась). Затем накрывалась крышкой с фторопластовой прокладкой и помещалась в пресс для полимеризации. В этом случае полная объемная концентрация дисперсной фазы не изменялась, и структура композита оставалась плотно упакованной.

В качестве дисперсионной среды использовалась модификация эпоксидной смолы L c отвердителем EPH 161 (соотношение смешивания в весовых частях 4:1). Клеевой состав замешивался с помощью электромеханического смесителя и далее диспергировался в ультразвуковой ванне Digital Ultrasonic Cleaner CD 4820 для дегазации смеси. Измерения массы смолы, отвердителя, необходимые для расчета концентрации смеси, выполнялись с помощью аналитических весов ЛВ-210А 2-го класса точности. Механические испытания выполнены на универсальной испытательной машине ZWIC Z-250. Образцы растягивались (сжимались) с постоянной скоростью 1 мм/мин. Напряжения измерялись при помощи датчика силы Xforce HP 2,5 кН, с точностью до 0,01 Н.

Для измерения деформации использовался микродатчик деформаций, установленный непосредственно на образец. Погрешность измерения величины деформаций порядка 0,01 %. Данные испытаний передавались на компьютер, по которым строились диаграммы зависимости удлинения образца от величины нагрузки. Анализ диаграмм позволяет определить область линейной деформации и рассчитать модуль Юнга, а также оценить предел прочности на разрыв и сжатие.

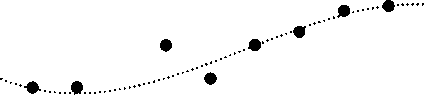
График зависимости предела прочности на разрыв для деформации растяжения приведен на рис. 7.

G max , ^МПа

0         20

% "мелких" частиц

Рис. 7. График зависимости предела разрушения при деформации растяжения от процентного содержания «мелких» частиц

Fig. 7. The graph of tensile fracture strength dependence on the fine particle percentage contents

Отметим, что значения коэффициента парной линейной корреляции для результатов измерения пористости (см. рис. 3) и данных по пределу разрушения при деформации (рис. 7) равно 0,574. То есть наблюдается явная прямая связь этих величин между собой.

Для измерения механической прочности на сжатие песок с нужной концентрацией «мелких» частиц заполнялся в цилиндрическую форму, после чего пропитывался под давлением клеевым составом и полимеризовался. И в этом случае полная объемная концентрация дисперсной фазы не изменялась, а структура композита оставалась плотно упакованной. Образцы для исследования имели, цилиндрическую форму размерами – 10×20 мм.

График зависимости предела разрушения при деформации сжатия от процентного содержания «мелких» частиц показан на рис. 8.

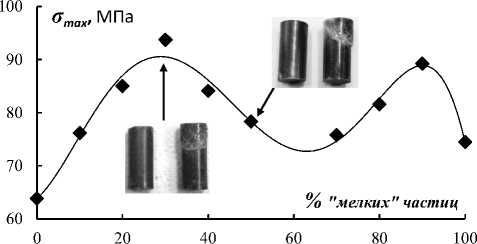
Рис. 8. График зависимости предела разрушения при деформации сжатия от процентного содержания «мелких» частиц

Fig. 8. The graph of fracture strength under compressive deformation dependence on the fine particle percentage contents

В этом случае коэффициент парной линейной корреляции с пористостью составлял –0,534. То есть в этом случае наблюдается явная обратная связь этих величин между собой.

Из графика видно, что наибольшие показатели предела разрушения характерны для составов, содержащий 30 и 90 % «мелких» частиц. Минимальному значению соответствует 60 % содержание «мелких» частиц. Аналогичные результаты с характерными минимумом и максимумом прочности на разрыв были получены в работе [30], где выполнялись исследования механических свойств композитов на основе эпоксидной смолы ДЭГ-1 с отвердителем ПЭПА в зависимости от концентрации отвердителя и кварцевого песка фракции 0,16– 0,315 мм.

Заключение

Приведено исследование физико-механических свойств композитного материала, состоящего из эпоксидной смолы и полидисперсной смеси кварцевого песка. В качестве дисперсного материала использовались смеси двух сортов кварцевого песка, с двумя средними диаметрами частиц: 0,15 и 0,53 мм. Построены гистограммы распределения частиц по размерам. Статистическая различимость ( t -критерий Стьюдента) этих двух выборок составила 102, что свидетельствует о статистической различимости этих двух выборок.

Измерены пористость и проницаемость смеси в зависимости от доли одного компонента в другом. Показано, что пористость каждого из компонентов имеет почти одинаковые значения, а зависимость смеси имеет минимум при 40 % содержании «мелкого» песка. Рассчитано изменение эффективного радиуса пор в зависимости от доли «мелких» частиц. Показано, что эта зависимость изменяется по параболическому закону с коэффициентом детерминации R ² ≈ 0,99.

Выявлена немонотонная зависимость предельной прочности полимеризованных образцов на растяжение и сжатие в зависимости от доли «мелких» частиц. Показано, что предельная прочность на растяжение имеет минимум при 30 % содержании доли «мелких» частиц.

При деформации сжатия наибольшие показатели предела разрушения характерны для составов, содержащих 30 и 90 % «мелких» частиц. Минимальному значению соответствует 60 % содержание «мелких» частиц.