Исследование свойств ограниченных гипергеометрических лазерных пучков

Новый тип световых мод – гипергеометрические (ГГ) моды недавно был представлен в работе [1]. ГГ-моды, как и моды Бесселя, обладают бесконечной энергией, следовательно, на практике их можно сформировать только приближенно и на конечном расстоянии.

Обобщение этих мод с добавлением гауссовой составляющей рассмотрено в работах [2-3]. Таким образом вводится понятие ГГ-пучков [3], энергия которых ограничена, но сами пучки теряют модовые свойства, сохраняя винтовую фазовую сингулярность.

Пучки с винтовой фазовой сингулярностью часто используют для передачи орбитального углового момента микрочастицам при оптическом манипулировании [4-7]. При этом, как правило, используются классические моды Гаусса-Лагерра, Бесселевы моды и чистые оптические вихри. Трехпараметрическое семейство ГГ-пучков [3] в отличие от указанных мод имеет больше параметров, позволяющих варьировать распределение интенсивности пучка в соответствии с нуждами микроманипулирования [8].

В данной работе проведено исследование возможности формирования гипергеометрических пучков методами дифракционной оптики. Также проведено сравнение их с ограниченными апертурой ГГ-модами.

где ( r, ф ) - полярные координаты входной плоскости, w и γ – действительные параметры логарифмического аксикона, σ – радиус перетяжки гауссова пучка, n – целый порядок спиральной фазовой сингулярности (топологический заряд), m – целое число.

Комплексная амплитуда (1) описывает световое поле с бесконечной энергией и с особенностью при r = 0 и m < 0. Однако при распространении в любой другой поперечной плоскости на расстоянии z от входной плоскости комплексная амплитуда уже не будет иметь особенности и будет конечной.

Преобразование Френеля от комплексной амплитуды (1) имеет следующий вид [3]:

. / x Г       A m+i Y г а л (-i)n+1 f z If V2g | Eу, n, m (P, 0 z) =^—Fl” I ---- X

2nn! (zq JI wq I

n ₂

f kGp I f ikp    . n Lx —=— exp ---+ in0 Г

( V2qz J     ( 2z J

n + m + 2 + i у

X (2)

^X i F

n + m + 2 + i у

_ f kGp I

¹ n ^{+ 11} -I V2 qz ^J

,

где (ρ, θ) – полярные координаты в плоскости на расстоянии z от входной, k =2π / λ – волновое число, Z - длина волны, z 0 = k a², q = ( 1 - iz 0/ z )^ш ; Г( x ) - гамма функция; 1 F 1 ( a,b;x ) – вырожденная (или конфлюэнтная) гипергеометрическая функция [10]:

1. Обобщенные гипергеометрические пучки

Обобщенные гипергеометрические лазерные пучки (ОГГ-пучки), рассмотренные в работе [3], представляют собой трехпараметрическое семейство функций. Они являются обобщением гипергеометрических мод [1] и двухпараметрических гипергеометрических пучков [9].

ОГГ-пучки имеют во входной плоскости ( z =0) следующий вид:

i Fi( a , b , x ) =      ^{Г (} b )     j t a ^{- 1}(1 - 1 ) ^b - a ^{- 1} exp( xt )d t . (3)

Г ( a ) Г ( b - a ) 0

Выражение (3) может также быть записано в виде ряда Тейлора (функция Куммера):

X i F( a, b, x) = E m =0

( a ) m x^m ( b ) _mm !^,

_ , х 1 f r I m     f r ² )

E у , n , m ⁽ r ¹ Ф )              exP ^ : ^X

2п IwJ     I 2a I

где ( a ) m = a ( a +1)( a +2)…( a + m -1) – символ Похгамме-ра, ( a ) 0 =1.

В выражениях (2) и (3) используется гамма функция для вещественного аргумента:

f . r , ■ I x exp I i у ln — + in ф I ,

I w J

x

Г ( x ) = J t^{x - 1} e ^{- 1} d t .

При y =0 и m =0 во входной плоскости будет поле:

,               1 I Г 2 1 X

E 0 n о ⁽ r , Ф ) = ^^e xp | -ТТ I exp ( in ф ) ^, 2 п    ( 2 с J

распространение которого описано как дифракция гауссового пучка на спиральной фазовой пластинке [11, 12].

При с^» (гауссовый пучок заменяется плоской волной) из (6) получаются оптические чистые вихри, описанные в [13].

При m = - 1 и с^» во входной плоскости будет поле:

1/ \ -1      /X

I r 1            I             r1

Ey n —1(r, ф) = —| — | exp| i Y ln — + in ф|, 2n I w)      I     w формирующее ГГ-моды [1].

• 2.    Реализация ГГ-мод

В [1] получено аналитическое решение параксиального волнового уравнения, названное ГГ-модами:

Во-вторых, амплитуда ГГ-мод при z =0 имеет особенность в нуле (неограниченно возрастает при r = 0), таким образом, необходимо также вырезание центральной области.

Поэтому на практике, чтобы сформировать ГГ-моду, световое поле (1) следует ограничить кольцевой диафрагмой с радиусами R ₁ и R ₂ ( R ₁<  R ₂), как показано на рис. 1.

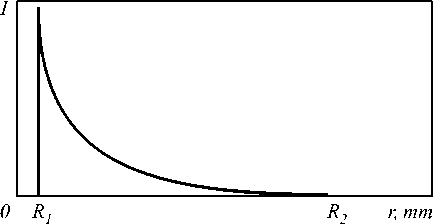
Рис. 1. Ограничение кольцевой апертурой радиального распределения интенсивности ГГ-моды во входной iH

_ .       .      1 I 2 z 1 2

E Y n ⁽ r , ф , z ) =      | —_T I x

2 n n ! I kw )

x exp

^x 1 F1

-—( n - i Y + 1)

I kr²

^ 2 z

n /2

I n + i y + 1 1

Г          x

I 2 |

n + 1 - i y

_ ikr ²1      .     .

, n +1;—— | exp( in ф ), 2 z )

плоскости

Однако такое ограничение апертуры начального поля при некоторых параметрах приводит к заметным искажениям ГГ-моды. На рис. 2 показан вид радиального распределения интенсивности поля (7), прошедшего расстояние z = 100 мм и его ограниченного апертурой аналога.

При следующих параметрах расчета: Х =532 нм, R 1 = 0,05 мм, R 2 = 1 мм, w = 1 мм, число отсчетов

принимающее при z=0 вид (7).

N = 512; параметры ГГ-моды: n = 4, y = - 10, сред-

Формирование ГГ-мод с помощью средств дифракционной оптики непростая задача. Во-первых, неквадратичное отклонение точной интенсивности, полученной на основе ур. (2), от рассчитанной с

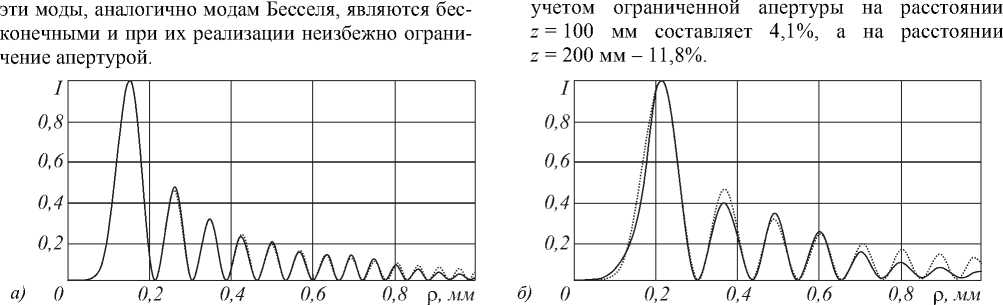
Рис. 2. Радиальное распределение интенсивности ГГ-моды ( у , n): ( - 10, 4) при z = 100 мм (а) и z = 200 мм (б): аналитический вид ГГ-моды (точечная кривая) и рассчитанный после ограничения апертурой (сплошная кривая)

Таким образом, с ростом расстояния погрешность увеличивается. Это связано с тем, что аналогично ограниченным Бесселевым пучкам ограниченные ГГ-моды сохраняют свои модовые свойства до некоторого расстояния [14].

• 3.    Определение зависимости сохранения модовых свойств

В [1] было показано, что это расстояние пропорционально следующей величине:

z =--- R2 г .

max   ctg (y/ R 2 )

Из этой формулы (8) следует, что при

R = 2y max n(2 n +1)

расстояние (9) принимает бесконечное значение. Однако это не так и пучок все равно теряет свои модовые свойства, начиная с некоторого расстояния.

Данный раздел посвящен эмпирическому определению этой зависимости от параметров лазерного из- лучения, оптического элемента и модовых параметров.

Моделировать распространение светового поля (7) для конечной апертуры можно, используя преобразование Ханкеля n -го порядка:

k                        ( ik p ^{2 1}

F (p, 0, z) = — exp(in 0)exp(ikz)exp       x n          z                         2z

,     .                    ^{V J} (11)

X

r I kr PI j I         I r d r ,

I z J

где J n ( r ) – функция Бесселя первого рода n -го порядка, P ( r ) – радиальная составляющая поля (7).

Параметры расчета были выбраны следующие: R 2 = 4 мм, число точек дискретизации 1024.

Сравнение полученных распределений интенсивности на расстоянии z = 1000 мм при различных значениях параметра у приведено на рис. 3, а для различных значений параметра n - на рис. 4.

Для приведенных параметров отличие аналитического решения от численного для радиального сечения интенсивности не превышает 4,5%.

Рис. 3. Радиальное сечение интенсивности для ГГ - мод ( у n): а) ( - 10,4) и б) (10,4) на расстоянии вдоль оси распространения z = 1000 мм (точечная линия – аналитическое решение, сплошная – преобразование Ханкеля)

Рис. 4. ГГ-моды ( у n): (3, - 7) и (3, 7) на расстоянии вдоль оси распространения z = 1000 мм а) радиальное сечение интенсивности (точечная линия – аналитическое решение, сплошная – преобразование Ханкеля), б) инвертированное распределение интенсивности, в) распределение фазы для моды (3, - 7), г) распределение фазы для моды (3, 7)

б)

в)                               г)

На рис. 3 и 4 хорошо видна зависимость радиуса центрального кольца в поперечном сечении пучка от модовых параметров у и n . При этом важен как модуль, так и знак параметра у : Как видно из рис. 3, изменение знака существенно влияет на радиус основного кольца пучка. В то время как знак номера винтовой фазовой сингулярности n влияет лишь на ориентацию спирального рисунка фазы, распределение интенсивности при этом совершенно не меняется.

В работе [15] было сделано предположение, что зависимость расстояния сохранения модовых свойств имеет характер, аналогичный Бесселевым модам:

z max

kR ₂

Однако серия численных экспериментов показала, что поведение ГГ-мод также зависит от знака параметра у .

На рисунках 5-8 показаны графики расстояния z_с , до которого в поперечной картине интенсивности пучка сохраняется хорошо выраженное центральное кольцо (в частности, периферийные кольца имеют интенсивность ниже, чем у центрального кольца) в зависимости от различных значений исследуемых параметров. Сохранение четко выраженного первого кольца представляет особый интерес в задачах оптического микроманипулирования [8], и данный критерий можно использовать для оценки сохранения структуры пучка, даже если среднеквадратичная погрешность существенна.

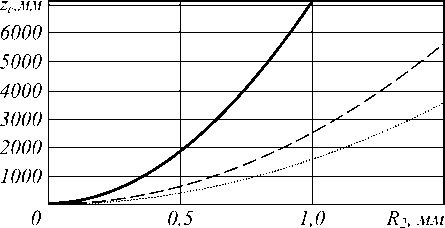
Рис. 5. Зависимость z_max от радиуса апертуры R₂ для ГГ-моды ( у n): ( - 5,4) -сплошная линия, ( - 7,4) -пунктирная линия, ( - 10,4) - точечная линия

для ГГ-моды ( у n): (5,4) -сплошная линия, (7,4) –пунктирная линия, (10,4) – точечная линия

Рис. 7. Зависимость zс от волнового числа k

Рис. 8. Зависимость zс от номера сингулярности n

Из графиков 5 и 6 легко видеть квадратичную зависимость z_c от радиуса апертуры R ₂ и обратную степенную от |у|.

Причем характер зависимости для отрицательных и положительных значений параметра у сильно отличается. График на рис. 7 демонстрирует линейную зависимость от волнового числа k , а рис. 8 показывает, что зависимости от номера сингулярности n фактически не имеется.

На основании приведенных выше рассуждений и подбора параметров по имеющимся данным была получена следующая формула для расстояния сохранения явно выраженного центрального кольца (при R 2 <1,5 мм):

c kR 2/ №’, Y> 0, c 2 ^kR 2/| Г, Y< 0,

где « 1 ® 0,5, c i ® 0,25, a ₂ ® 2,3, c ₂ ® 25.

Любопытно отметить, что пучки с отрицательными, но небольшими по абсолютному значению параметрами у существенно дольше сохраняют свои модовые свойства.

По формуле (13) расстояние сохранения центрального кольца ограниченной ГГ-моды из раздела 2 (длина волны Х =532 нм, R ₂ = 1 мм, n = 4, у = - 10) составляет z_c ~ 1500 мм, в то время как по формуле (12) расстояние сохранения модовых свойств несколько меньше z max ~ 1180 мм.

Таким образом, несмотря на то, что уже при z =200 мм погрешность составила около 12%, четко выраженное центральное кольцо сохраняется гораздо дольше.

На рис. 9 показано распространение ГГ-мод (длина волны Х =532 нм, R ₂ = 4 мм, n = 4, у = ± 10) с противоположными знаками параметра у , выполненное с помощью преобразования Ханкеля. Чтобы основное кольцо входило в поле зрения, радиус рассчитываемой картины R o увеличивался по мере увеличения расстояния z .

Как видно из рисунка 8, оценка (13) здесь дает неправильный результат: для у = - 10 получается z_c ~ 24000 мм, на самом же деле структура уже разрушена при z = 20000 мм, для у =10 получается z_c ~ 15000 мм, на самом же деле центральное кольцо все еще достаточно выражено при z = 20000 мм.

Видимо, при значениях радиуса R 2 > 1,5 мм зависимость становится несколько иная, чем полученная в (13).

Интересно отметить динамику изменений ГГ-мод с противоположными знаками параметра у . В зоне дифракции Френеля центральные кольца пучков имеют значительно различающийся диаметр - меньший для отрицательного у . Затем, при распространении их поперечные сечения становятся все более схожими, пока в дальней зоне не будут совершенно идентичными по распределению интенсивности.

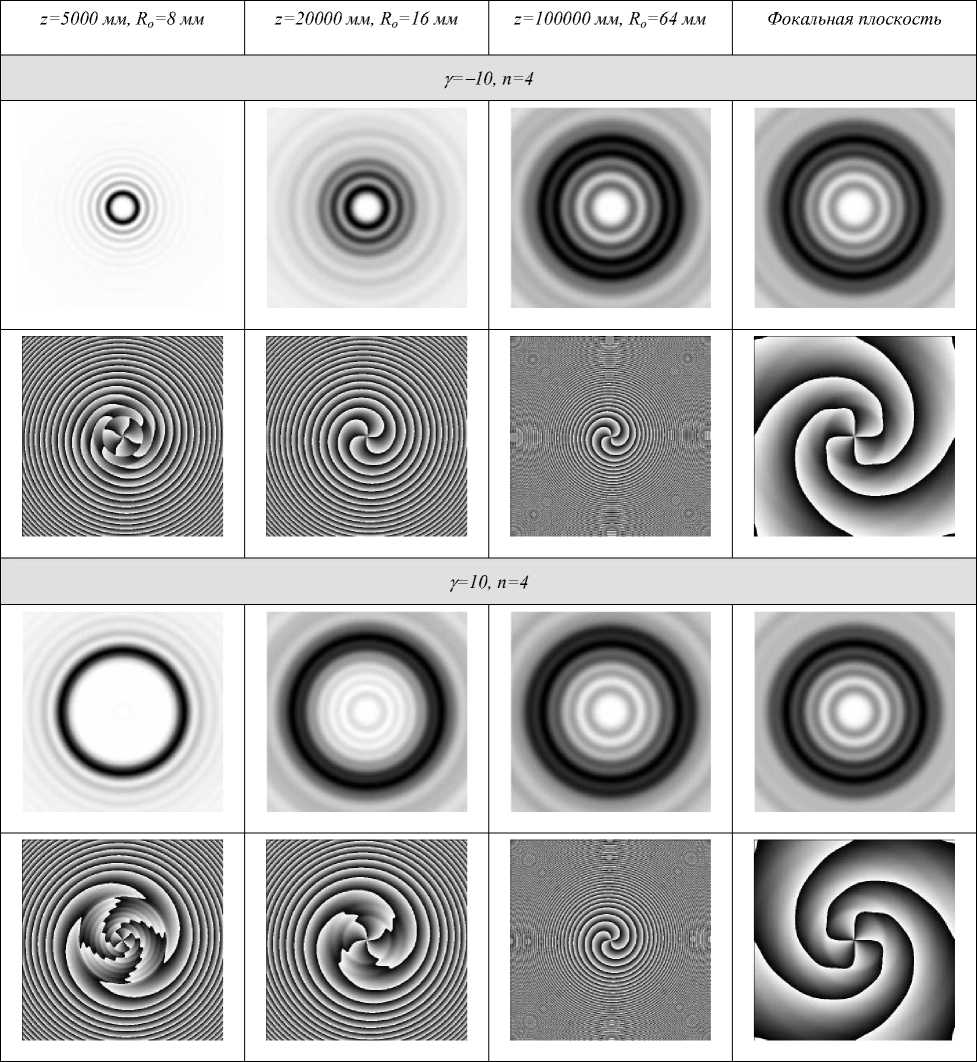
Рис. 9. Сравнение распространения ГГ-мод с противоположными знаками параметра γ

4.    Сравнение дифракционных свойств ограниченных ГГ-мод и ОГГ-пучков

Как следует из раздела 1, ГГ-моды являются частным случаем ОГГ-пучков при m = - 1 и σ→∞ (см. формулу (7)). Однако при формировании ГГ-мод неизбежно приходится сталкиваться с их ограниченными аналогами. В частности, в разделах 2 и 3 было рассмотрено ограничение поперечно бесконечного входного поля апертурой. В этом разделе проводится сравнение такого ограничения с наложением гауссовой функции, т.е. с ОГГ-пучком при m = - 1 и σ =const.

На рис. 10 приведено сравнение распространения ОГГ-пучков и ограниченных ГГ-мод. Параметры расчетов такие же, как в разделе 3, радиус гауссово-го пучка σ выбран так, чтобы размеры основного кольца пучков совпадали на расстоянии z =1000 мм .

Как видно из двух первых строк рис. 10, несмотря на существенные значения среднеквадратичного отклонения ограниченной ГГ-моды от ее аналитического вида, структура пучка сохраняется вплоть до z=10000 мм, что составляет 1250 входных апертур. При этом ОГГ-пучок с аналогичными параметрами разрушается значительно быстрее – уже при z=2000 мм, что составляет 250 входных апертур. Согласование численных результатов с теоретическими для ОГГ-пучков очень хорошее – погрешность не выше 2%.

На рис. 11 показано более подробно сравнение динамики изменения радиального сечения ограниченной ГГ-моды и ОГГ-пучка на расстояниях от z =500 мм до z =2000 мм.

	z=1000 мм	z=2000 мм	z=5000 мм	z=10000 мм
ГГ-мода ( γ , n): ( - 10, 4)
Q £ at	о	©		/^8St\
at tl		@	^^^^^^^	lOi
δ , %	16,2	18,8	30,7	33,4
ОГГ-пучок ( γ , n,m ): (-10, 4, -1)
Q % 3 at		©
at tl		©
δ , %	1,6	0,3	0,08	0,15

Рис 10. Сравнение распространения ОГГ-пучков и ГГ-мод: аналитические и численные результаты

Из рисунка 11 хорошо видно, что ГГ-моды даже в случае ограничения апертурой значительно дольше сохраняют свою структуру, чем ОГГ-пучки.

Однако в отличие от ГГ-мод ОГГ-пучки имеют на один параметр больше, что дает больше свободы при формировании различных типов сингулярных пучков.

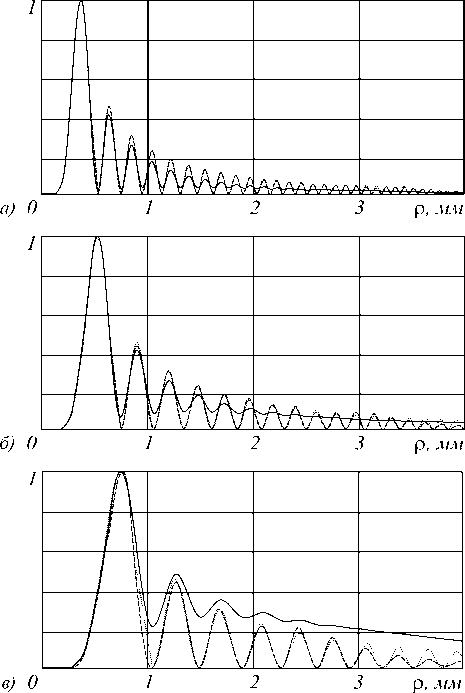
Рис. 11. Радиальное сечение интенсивности для ГГ - моды ( γ , n)=( - 10,4) (точечная линия – аналитическое решение, пунктирная – преобразование Ханкеля) и ОГГ-пучка ( γ , n,m)=( - 10, 4, - 1) (сплошная линия) на расстоянии вдоль оси распространения z = 500 мм (а), z = 1000 мм (б), z = 2000 мм (в)

На рис. 12 показаны примеры ОГГ-пучков с различными значениями параметра m на расстоянии z = 1000 мм: ( γ , n , m )=( - 10, 4, - 2), ( - 10, 4, - 1), ( - 10, 4, 0), ( - 10, 4, 2).

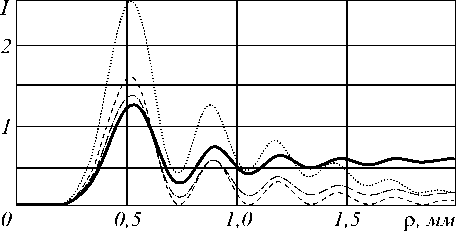
Рис. 12. Радиальное сечение интенсивности для ОГГ-пучка на расстоянии вдоль оси распространения z = 100 мм для ( γ , n,m): ( - 10, 4, - 2) – сплошная линия, ( - 10, 4, - 1) – штрих-пунктирная линия, ( - 10, 4, 0) – пунктирная линия, ( - 10, 4, - 2) – точечная линия

Из рис. 12 видно, что с увеличением значения параметра m энергия пучка все больше концентрируется в центральной части (рост центрального кольца не совсем корректно отражает динамику этой концентрации, так как входное поле по энергии не нормировалось).

Заключение

В заключении кратко сформулируем полученные результаты.

• •    Показана возможность аппроксимации ГГ-мод их ограниченными аналогами с точностью 5-12% до некоторого расстояния.

• •    Получена аналитическая формула при небольших значениях входной апертуры для оценки расстояния, на котором сохраняется четко выраженное центральное кольцо моды.

• •    Отмечено, что ГГ-моды, имеющие противоположные знаки параметра γ , имеют различные диаметры центральных колец в зоне дифракции Френеля, которые, однако, в дальней зоне дифракции становятся совершенно одинаковыми.

• •    Обобщенные ГГ-пучки, согласованные с параметрами ГГ-мод, сохраняют свою структуру на значительно меньшем расстоянии. Однако дополнительный параметр m позволяет варьировать концентрацию энергии таких пучков в центральной части.

Работа выполнена при частичной финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), грантов РФФИ №№ 07-07-97600, 08-07-99007 и гранта Президента РФ по поддержке ведущих научных школ (НШ-3086.2008.9).